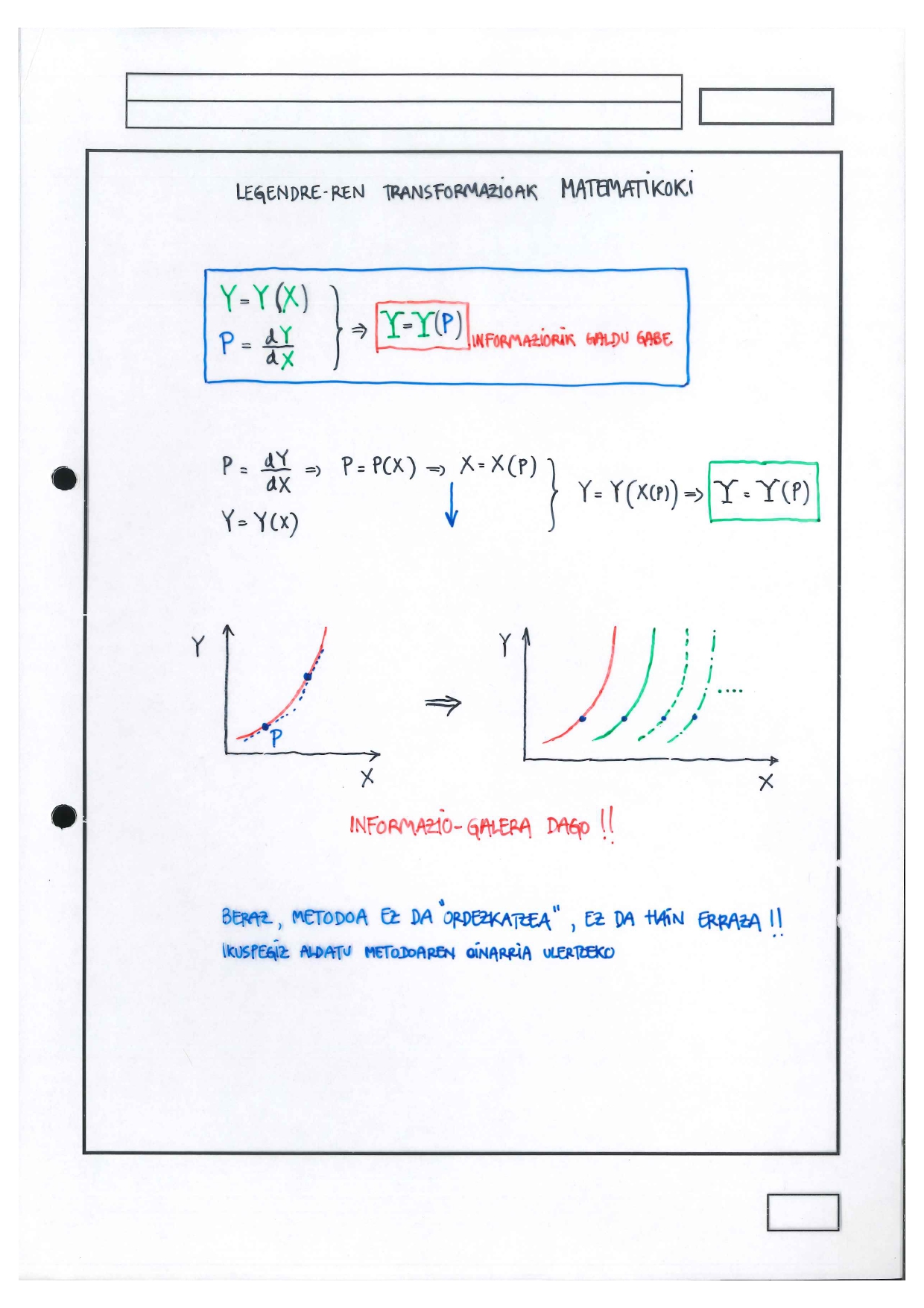
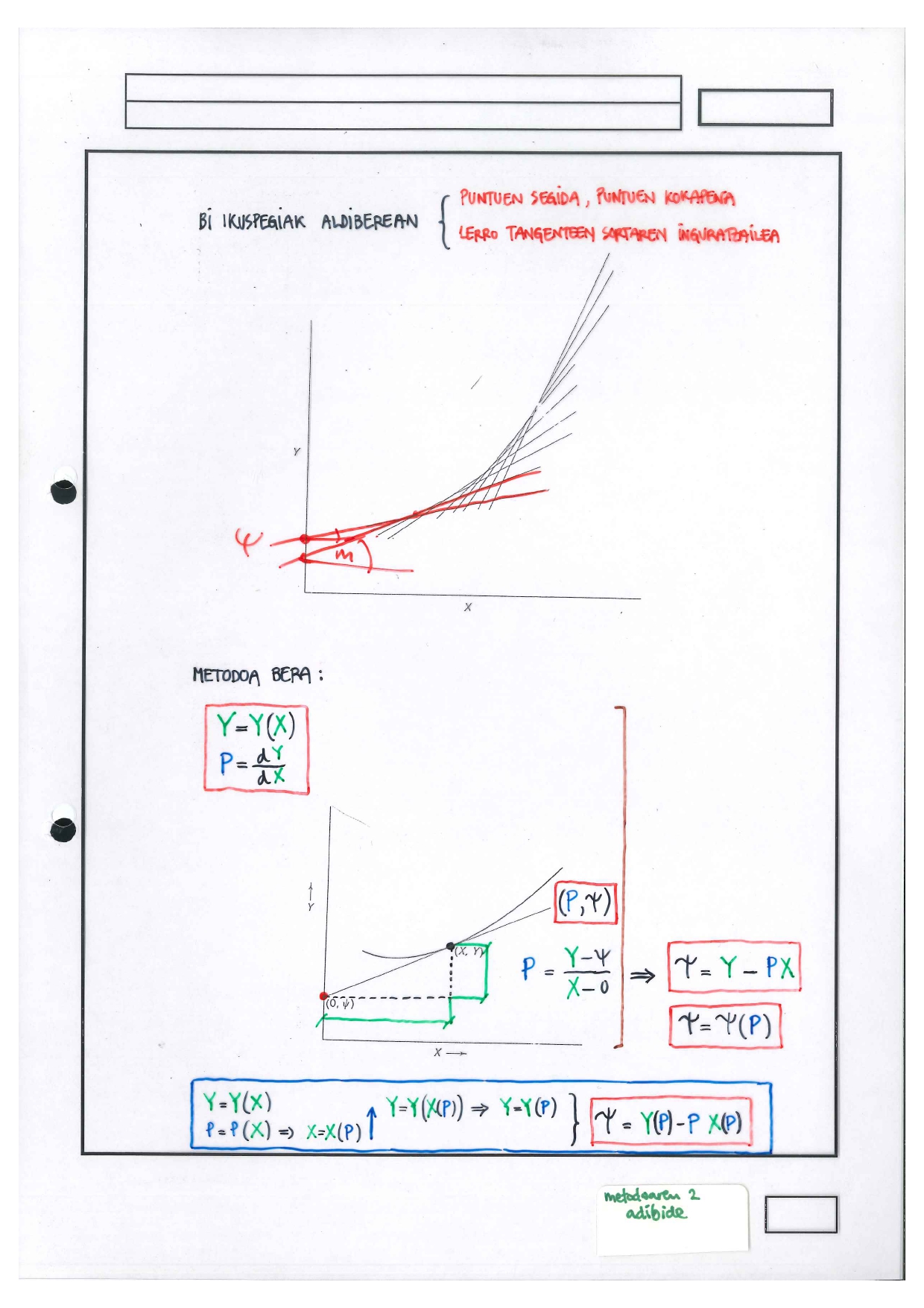
Apunteak

08 Gaia: Formalismo-aldaketa

---

Sarrera

8. Gaia: Apunteak

8. Gaia:, C-5, C-6, C-7

Postulatuak

• 8.1 Sarrera: Postulatuak eta Printzipioak

  

  • 1. postulatua

    

  • 2. postulatua

    

  • 3. postulatua

    

Prozesuak

• 8.2 Prozesuak:

  

  • Iruzinak:

    • oinarrizko ekuazioa

    • egoera-ekuazioak

    • oinarrizko ekuazioaren aurpegiak:

    

    • entropikoa

    • energetikoa

• Adibideak, ariketak, kalkuluak

  

  • Ondoko bi adibideetan oinarrizko ekuazio hipotetikoak proposatzen dira eta horietatik abiatuta egoera-ekuazioak lortu behar dira.

  • Formalismo berrian, oinarrizko ekuazioan sistemari buruzko informazio dena dago, besteak beste, egoera-ekuazioak: egoera-ekuazioak dira oinarrizko ekuazioaren lehen deribatuak.

  • Oinarrizko ekuazioaren aldagai independenteak dira sistemaren aldagai estentsiboak eta horiekiko deribatuak dira bakoitzarekin lotutako aldagai intentsiboa eta, esan bezala, lortutako ekuazioa da askatasun-gradu horrekin lotutako egoera-ekuazioa:

  $${\left(\frac{\partial U}{\partial X_i}\right)}_{X_{j\ne i}}\equiv P_i=P_i(\left\{X_i\right\})$$

  • $i$, $[P_i,X_i]$ askatasun-graduarekin lotutako egoera-ekuazioa

  • 1 adibidea: $U=\left(\frac{v_0\theta }{R^2}\right)\frac{S^2}{NV}$, $\boxed{{\displaystyle U=C\frac{S^2}{NV}}}$

    • Osagai bakarreko sistema hidrostatikoari dagokion oinarrizko ekuazioa adierazpen energetikoan (printzipioz!)

    • Kontuz, lehenengo puntua da egiaztatzea benetako oinarrizko ekuazioa den. Kasu honetan, ez da, ez baita da lehen ordenako funtzio homogeneoa, hots, estentsiboak diren aldagaiak (formalismoaren arabera, aldagai independente denak, esan bezala) bider $\lambda$ parametroa erabilita biderkatuz gero, funtzioa bera, $U$, bider $\lambda$ parametroaz biderkatuta agertu beharko da. Ez da hori gertatzen.

    • Egiaztatzea:

      • $\lambda \times (S,V,N)\to U^{\prime }=C\frac{(\lambda S{)}^2}{(\lambda N)(\lambda V)}\Rightarrow U^{\prime }=C\frac{S^2}{NV}\frac{{\lambda }^2}{\lambda \lambda }\Rightarrow U^{\prime }=C\frac{S^2}{NV}$

      • $S$ aldagairen berretura $3$ da:

      • $\lambda \times (S,V,N)\to U^{\prime }=C\frac{(\lambda S{)}^3}{(\lambda N)(\lambda V)}\Rightarrow U^{\prime }=C\frac{S^3}{NV}\frac{{\lambda }^3}{\lambda \lambda }\Rightarrow U^{\prime }=\lambda C\frac{S^3}{NV}\Rightarrow U^{\prime }=\lambda U$

    • Honako hauek dira askatasun-gradu termikoarekin, mekanikoarekin eta kimikoarekin lotutako egoera-ekuazioak:

      1. egoera-ekuazio termikoa: ${\left(\frac{\partial U}{\partial S}\right)}_{V,N}\equiv T(S,V,N)=3C\frac{S^2}{NV}$

      2. egoera-kuazioa mekanikoa: ${\left(\frac{\partial U}{\partial V}\right)}_{S,N}\equiv -p(S,V,N)=-C\frac{S^3}{N{V}^2}$

      3. egoera-ekuazio kimikoa: ${\left(\frac{\partial U}{\partial N}\right)}_{S,V}\equiv \mu (S,V,N)=-C\frac{S^3}{N^{2}V}$

  • 2 adibidea: $u=\left(\frac{v_0^{\frac{1}{2}}\theta }{R^{\frac{3}{2}}}\right)\frac{s^{\frac{5}{2}}}{v^{\frac{1}{2}}}$, $\boxed{{\displaystyle u=C\frac{s^{\frac{5}{2}}}{v^{\frac{1}{2}}}}}$

    • Osagai bakarreko sistema hidrostatikoari dagokion oinarrizko ekuazio molarra: adierazpenean agertzen diren aldagai denak molarrak baitira: $u$, barne-energia bera; $s,v$.

    • Printzipioz, osagai bakarreko sistema hidrostatikoak 3 askatasun-gradu dauzka eta, formalismo berriaren arabera, horiekin lotutako aldagai estentsiboek agertu behar dira aldagai independenteen sortan. Kasu honetan, aldagai independenteen sortan 2 aldagai $(s,v)$ molar, beraz, intentsibo baino ez dira agertzen.

    • Horren arabera, 2 egoera-ekuazio baino ezin izango dira ondorioztatu?

    • Oraingo honetan, era inplizituan emanda dago oinarrizko ekuazio osoa, hots, sistema osoari dagokiona eta ez masa-unitatekoari dagokiona.

    • $U$-ren adierazpena, lehen ordenako funtzio homogeneoa izanik, hots, estentsibo eta biderkatzeko parametroa (fisikoki, sistemaren kopia egiteko modua) edozein izan daitekeenez, batzuetan, balio berezia izan dezake: $\lambda =\frac{1}{N}$: balio honek molar bihurtzen du oinarrizko ekuazioa, batetik, eta, bestetik, desagertarazten du $N$ aldagaia aldagai independenteen sortatik:

    • $[\lambda \equiv \frac{1}{N}]\times (S,V,N)=(\lambda \cdot S=\frac{S}{N}=s,\lambda \cdot V=\frac{V}{N}=v,\lambda \cdot N=\frac{N}{N}=1,)=(s,v,1)\equiv (s,v)$

    • Orduan, prozedura horrek guztiak bidea ematen du, alderantzizko noranzkoan, oinarrizko ekuazioaren adierazpen molarretik benetako oinarrizko ekuazioa ondorioztatzeko, agertaraziz $N$ aldagaiarekiko mendekotasuna: $$(u\equiv \frac{U}{N},s\equiv \frac{S}{N},v\equiv \frac{V}{N})$$

    • $u=C\frac{s^{\frac{5}{2}}}{v^{\frac{1}{2}}}\Rightarrow \frac{U}{N}=C\frac{{\left(\frac{S}{N}\right)}^{\frac{5}{2}}}{{\left(\frac{V}{N}\right)}^{\frac{1}{2}}}\Rightarrow U=C\frac{S^{\frac{5}{2}}}{V^{\frac{1}{2}}}\cdot N$

Termodinamikaren Oinarrizko Problema: printzipio estremala

• 8.3 Termodinamikaren Oinarrizko Problema: Printzipio Estremala

  

  • Printzipio estremalaren erabileraren 2 adibide:

    

    • entropia maximoa

    • energia minimoa

Oinarrizko Ekuazioa: propietateak eta eraikuntza

• 8.4 Oinarrizko Ekuazioaren propietateak

  • Euler-en ekuazioa:

    

    • Lehen ordenako funtzio homogeneoa

  • Gibbs-en eta Duhem-en erlazioa:

    

    • Zero ordenako funtzio homogeneoa

    • parametro intentsiboak ez dira independente

  • Iruzkinak:

    • Euler-en erlazioaren eta Gibbs-en eta Duhem-en ekuazioaren jatorria da oinarrizko ekuazioa lehen ordenako funtzio homogeneotasuna

    • Aipatutako bi horien bidez oinarrizko ekuazioa eraiki daiteke sistemari dagozkionn egoera-ekuazio bat faltan dagoenean

      • Kontuz: nahiz eta aipatu den oinarrizko ekuazioa eraiki daitekeela, ez da (guztiz) egia, ez baitira egoera-ekuazio denak ezagutzen: hipotesia da haietako bat faltan dagoela. Baina berreskuratu ahal izango da ia-ia oinarrizko ekuazio osoa, integrazio-konstante bat salbu

      • Hots, sistemari buruzko informazio gehigarria izanez gero, esaterako, oreka-egoeraren bat, orduantxe izango da integrazio-konstantearen balio

    • Egoera-ekuazioetako bat faltan dagoenean (normalean, beti faltako da askatasun-gradu kimikoarekin lotutakoa) oinarrizko ekuazioa lortzeko bi horiek erabiltzea ez da modu bakarra, edo beti erabili behar dena edo errazena.

      • Beti integratu daiteke oinarrizko ekuazio molarraren adierazpen diferentziala.

  • ezaugarrien/propietateen laburbilduma

    

• Oinarrizko ekuazioaren eraikuntzaren prozeduraren adibideak: proposatutako ariketak

  • Ondorengo ariketetan, osagai bakarreko sistema hidrostatiko hipotetikoekin lotutako 2 egoera-ekuazio ezagunak dira eta, kasu denetan, oinarrizko ekuazioa eraiki egin behar da.

  • Horretarako, arestian aipatutako metodoa erabili behar da:

    • Zeharkako metodoa:

      • Gibbs-en eta Duhem-en erlazioaren bidez falta den 3. egoera-ekuazioa lortu

        • $d\mu =-sdT+vdp$ (adierazpen energetikoan)

      • $d\left(\frac{\mu }{T}\right)=s\cdot d\left(\frac{1}{T}\right)+v\cdot d\left(\frac{p}{T}\right)$ (adierazpen entropikoan)

      • Euler-en ekuazioan injektatu 3 egoer-ekuazioak

        • $U=T\cdot S-p\cdot V+\mu \cdot N$ (adierazpen energetikoan)

        • $S=\left(\frac{1}{T}\right)\cdot U+\left(\frac{p}{T}\right)\cdot V-\left(\frac{\mu }{T}\right)\cdot N$ (adierazpen entropikoan)

    • Zuzenean: oinarrizko ekuazio molarra integratuz

      • $du=T\cdot ds-p\cdot dv$ (adierazpen energetikoan)

      • $ds=\left(\frac{1}{T}\right)\cdot du+\left(\frac{p}{T}\right)\cdot dv$ (adierazpen entropikoan)

  • 1. Ariketa:

    1. $T=3A{\displaystyle \frac{s^2}{v}}$

    2. $p=A{\displaystyle \frac{s^3}{v^2}}$

    • emaitza: $\boxed{{\displaystyle U=A{\displaystyle \frac{S^3}{VN}}+N\mathrm{k}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.}}$

  • Zeharkako metodoa:

  • Gibbs-en eta Duhem-en erlazioa erabiliz

    $d\mu =-sdT+vdp$

    1. $T=3A{\displaystyle \frac{s^2}{v}}\Rightarrow \{dT=3A[\frac{2s}{v^2}ds+s^2\left(\frac{-1}{v^2}\right)dv]\}\times (-s)$ $dT=3A[\frac{2s}{v}ds-\frac{s^2}{v^2}dv]$

    2. $p=A{\displaystyle \frac{s^3}{v^2}}\Rightarrow \{dp=3[\frac{3s^2}{v^2}ds+s^3\left(\frac{-1}{v^4}\right)2vdv]\}\times v$ $dp=3A[\frac{3s^2}{v^2}ds-\frac{2s^3}{v^3}dv]$
       $d\mu =A[\frac{-3s^2}{v}ds+\frac{s^3}{v^2}dv]\Rightarrow \int d\mu \equiv \mu =-A\int \frac{3s^2}{v}ds+f(v)\to \boxed{{\displaystyle \mu =-A\frac{s^3}{v}+f(v)}}$
       ${\left(\frac{\partial \mu }{\partial v}\right)}_s=\boxed{{\displaystyle -A{s}^3\left(\frac{-1}{v^2}\right)+f^{\prime }(v)}}\to =A\left(\frac{s^3}{v^2}\right)\Rightarrow f^{\prime }(v)=0\Rightarrow f(v)=C$
       $\boxed{{\displaystyle \mu =-A\frac{s^3}{v}+{\mu }_0}}$

  • Euler-en ekuazioan injektatuz:

    $U=T\cdot S-p\cdot V+\mu \cdot N$ edo $u=T\cdot s-p\cdot v+\mu$

    $u=3A\frac{s^3}{v}-A\frac{s^3}{v}-A\frac{s^3}{v}\Rightarrow \boxed{{\displaystyle u=A\frac{s^3}{v}+C}}\Rightarrow \frac{U}{N}=A\frac{{\left(\frac{S}{N}\right)}^3}{\left(\frac{V}{N}\right)}+C\Rightarrow \boxed{{\displaystyle U=A{\displaystyle \frac{S^3}{VN}}+NC}}$

  • 2. Ariketa:

    1. $U=pV$

    2. $p=B{T}^2$

    • emaitza: $\boxed{{\displaystyle S=2B^{1/2}{V}^{1/2}{U}^{1/2}-{\left({\displaystyle \frac{\mu }{T}}\right)}_{0}N}}$

  • Zeharkako metodoa:

  • Gibbs-en eta Duhem-en erlazioa erabiliz

    $d\left(\frac{\mu }{T}\right)=ud\left(\frac{1}{T}\right)+vd\left(\frac{p}{T}\right)$

    1. $\frac{1}{T}=B^{\frac{1}{2}}{v}^{\frac{1}{2}}{u}^{-\frac{1}{2}}\Rightarrow \{d\left(\frac{1}{T}\right)=B^{\frac{1}{2}}[\frac{1}{2}{v}^{-\frac{1}{2}}{u}^{-\frac{1}{2}}dv+\frac{-1}{2}{v}^{\frac{1}{2}}{u}^{-\frac{3}{2}}du]\}\times (u)$ $d\left(\frac{1}{T}\right)=B^{\frac{1}{2}}[\frac{1}{2}{v}^{-\frac{1}{2}}{u}^{\frac{1}{2}}dv-\frac{1}{2}{v}^{\frac{1}{2}}{u}^{-\frac{1}{2}}du]$

    2. $\frac{p}{T}=B^{\frac{1}{2}}{v}^{-\frac{1}{2}}{u}^{\frac{1}{2}}\Rightarrow \{d\left(\frac{p}{T}\right)=B^{\frac{1}{2}}[-\frac{1}{2}{v}^{-\frac{3}{2}}{u}^{\frac{1}{2}}dv+\frac{1}{2}{v}^{-\frac{1}{2}}{u}^{-\frac{1}{2}}du]\}\times (v)$ $d\left(\frac{p}{T}\right)=B^{\frac{1}{2}}[-\frac{1}{2}{v}^{-\frac{1}{2}}{u}^{\frac{1}{2}}dv+\frac{1}{2}{v}^{\frac{1}{2}}{u}^{-\frac{1}{2}}du]$
       $d\mu =0\Rightarrow \int d\left(\frac{\mu }{T}\right)\equiv \boxed{{\displaystyle \left(\frac{\mu }{T}\right)={\left(\frac{\mu }{T}\right)}_0}}$

  • Euler-en ekuazioan injektatuz:

    $S=\left(\frac{1}{T}\right)\cdot U+\left(\frac{p}{T}\right)\cdot V-\left(\frac{\mu }{T}\right)\cdot N$ edo $s=\left(\frac{1}{T}\right)\cdot u+\left(\frac{p}{T}\right)\cdot v-\left(\frac{\mu }{T}\right)$

    $s=B^{\frac{1}{2}}{v}^{\frac{1}{2}}{u}^{-\frac{1}{2}}u+B^{\frac{1}{2}}{v}^{-\frac{1}{2}}{u}^{\frac{1}{2}}v-{\left(\frac{\mu }{T}\right)}_0\Rightarrow \boxed{{\displaystyle s=2B^{\frac{1}{2}}{v}^{\frac{1}{2}}{u}^{\frac{1}{2}}-{\left(\frac{\mu }{T}\right)}_0}}\Rightarrow \frac{S}{N}=2B^{\frac{1}{2}}{\left(\frac{V}{N}\right)}^{\frac{1}{2}}{\left(\frac{U}{N}\right)}^{\frac{1}{2}}-{\left(\frac{\mu }{T}\right)}_0\Rightarrow$ $S=2B^{\frac{1}{2}}{\left(\frac{V}{N}\right)}^{\frac{1}{2}}{\left(\frac{U}{N}\right)}^{\frac{1}{2}}-{\left(\frac{\mu }{T}\right)}_0\Rightarrow \boxed{{\displaystyle S=2B^{\frac{1}{2}}{V}^{\frac{1}{2}}{U}^{\frac{1}{2}}-{\left(\frac{\mu }{T}\right)}_{0}N}}$

  • 3. Ariketa:

    1. $u={\displaystyle \frac{3}{2}}pv$

    2. $u^{1/2}=BT{v}^{1/3}$

    • emaitza: $\boxed{{\displaystyle S=2B{V}^{1/3}{U}^{1/2}{N}^{1/6}+N{s}_0}}$

  • Zuzenean, oinarrizko ekuazio molarra integratuz:

  • 4. Ariketa:

    1. $U={\displaystyle \frac{1}{2}}pV$

    2. $T^2=A{\displaystyle \frac{U^{3/2}}{V{N}^{1/2}}}$

    • emaitza: $\boxed{{\displaystyle S=4A^{-1/2}{U}^{1/4}{V}^{1/2}{N}^{1/4}+S_0}}$

• Gas idealaren oinarrizko ekuazioa lortu

  $$\boxed{{\displaystyle S=N{s}_0+NR\ln \left[{\left(\frac{U}{U_0}\right)}^c\left(\frac{V}{V_0}\right){\left(\frac{N}{N_0}\right)}^{-(c+1)}\right]}}$$

• van der Waals-en fluidoari dagokion oinarrizko ekuazioa lortu

  $$\boxed{{\displaystyle S=NR\ln [(v-b){(u+\frac{a}{v})}^c]+N{s}_0}}$$

Printzipio estremalaren aukerako formulazioak

• Aukerako formulazioak, baliokidetasuna

  

• 

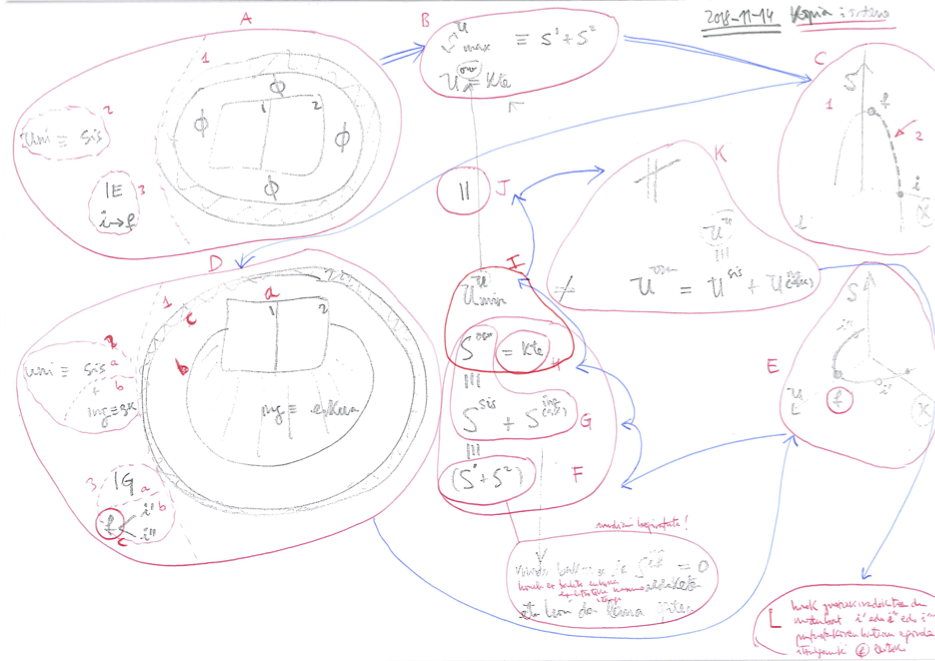
  Baliokidetasunaren esangura fisikoa.

• Postulatuetan onartutako ezaugarriei esker, posiblea da edozein sistemaren kasuan oinarrizko ekuazioaren adierazpen entropikotik adierazpen energetikora pasatzea, gutxienez, era formalean.

  • Propietate horrek simetrikotasuna ematen dio formalismoari oinarrizko ekuazioari dagokionez.

  • Horrek garrantzia handia dauka, aldagai independenteen sorta ezberdina izanik oinarrizko ekuazioaren adierazpenetan, prozesuak gertatzen diren baldintza esperimentaletara moldatu ahal izango baita oinarrizko ekuazioaren erabilera; hots, baldintza esperimentalek esango dute oinarrizko ekuazioaren zein adierazpen erabili.

  • Termodinamikaren oinarrizko problema ebazteko tresna postulatuetan dago: $S$ entropiaren printzipio estremala, hau da: barne-loturaren bat askatutakoan, sistemaren aldagai estentsiboek haien balioak aldatuko dituzte, $S$ entropia maximizatzeko asmotan eta entropia maximoa den egoeran sistemaren aldagai intentsiboen balioak berdinak izango dira (aldagai estentsiboak dira barne-lotura askatutakoan askatu direnak eta, intentsiboak, horiekiko konjokatuak direnak).

  • Orduan, baldintza esperimentalek esango badute oinarrizko ekuazioaren zein adierazpen den egokiago, baina $S$ entropiaren kasuan baino ez badago printzipio estremala, adierazpenaz aldatutakoan, printzipioa bera transladatu beharko litzateke, prozesua gertatu den baldintza esperimentaletan egokia den ekuazioari dagokion printzipio estremala (oraingoz, aukera bakarra da $U$-ri dagokiona) erabiliz iragartzeko bukaerako oreka-egoera…horixe da honen guztiaren xedea: prozesua gertatu den baldintza esperimentaletan $(S,V,N)$ aldagai independenteen sorta egokiena denean $S$-ren printzipio estremala trasladatzea $U$-ra.

  • Egingo den translazioaren jatorrian honako propietate hau dago:

    edozein sistemaren kasuan, edozein oreka-egoera, barne-energia konstanteko eta entropia maximoko oreka-egoera moduan zein entropia konstanteko eta energia minimoko oreka-egoera moduan interpretatu daiteke

  • Edozein kasutan, kontuan hartu behar da, Printzipioak bete behar direla, hots:

    • 1. Printzipioa: energiaren kontserbazioaren printzipioa Posibleak dira energia kontserbatuko duten prozesuak Guztiz isolatutako sistemaren, unibertsoaren, energia kontserbatzen da (Formalismo berrian ez da esplizituki aipatu lehen printzipioa…)

    • 2. Printzipioa: asimetria dago Izadian Berez gertatzen diren prozesuak noranzko bakarrean gertatzen dira Guztiz isolatutako sistemaren, unibertsoaren, entropiak gora egiten du berezko prozesuetan

  • Unibertsoaren $S$ entropia maximoa da

    

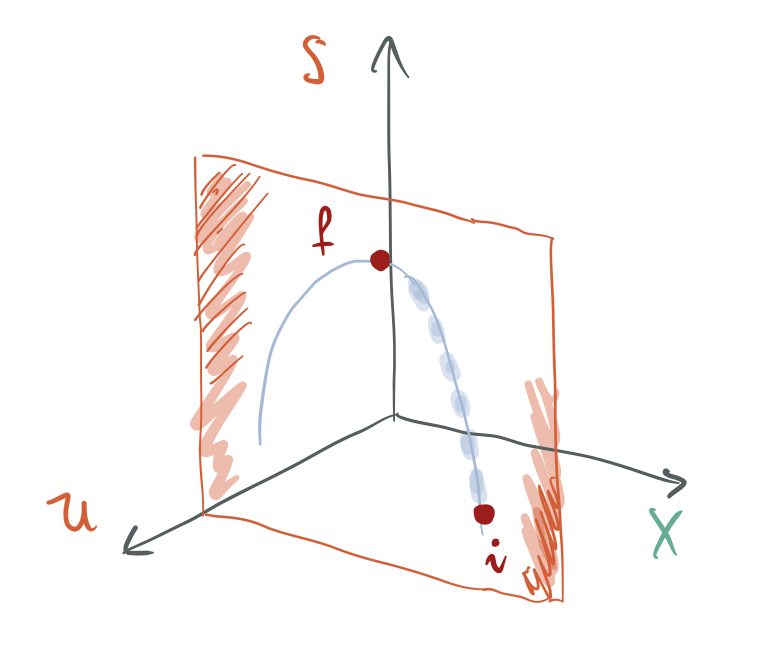
    Baliokidetasunaren esangura fisikoa.

  • Sistema konposatua da aztertuko den sistema eta, gainera, guztiz isolatutakoa, beraz, unibertsoa, ez dauka ingurunerik. Unibertsoa denez, edozein prozesutan unibertsoaren energia kontserbatzen denez, sistemaren energia kontserbatuko da: $U^{sis}=k$.

  • Sistema dago entropiaren gainazaleko punturen batean, zeinari dagokion energia den finkatutako energia $U^{sis}$, hots: sistema dagoen hasierako $i$ oreka-egoera da $S$-gainazalaren eta $U^{sis}$-planoaren arteko ebakidura kurban, irudian adierazita dagoenez.

  • Barne-loturaren bat askatuko da (iruditik agerikoa denez, $X$ aldagai estentsiboari dagokion askatasun-gradua baino ez da askatu, horixe baita, ezarritako baldintzatan, sistemak efektiboki duen askatasun-gradu bakarra) eta iragarri nahi da bukaerako oreka-egoera zein den.

  • Berez eboluzionatzen utziko zaio sistemari (unibertsoari) eta, beraz, prozesu itzulezina eragingo da (ezin da irudian adierazi, ez baita kuasiestatiko, definizioz), baina bukaeraraino eboluzionatzen utziz gero, bukaerako egoeran unibertsoaren, sistemaren, entropia maximoa izango da: $f$ egoera, irudian.

  • Sistemaren $U$ barne-energia minimoa da

    

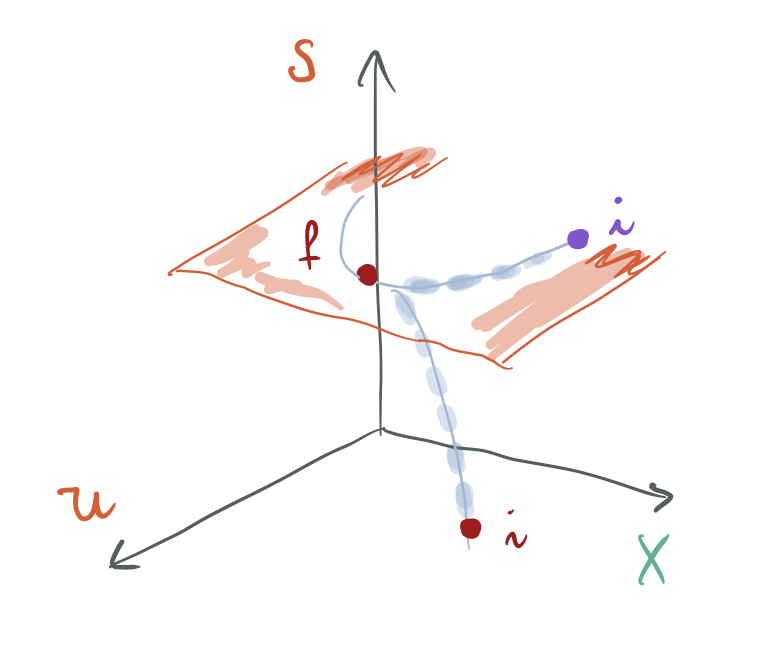
    Baliokidetasunaren esangura fisikoa.

  • Aurreko prozesuko bukaerako $f$ oreka-egoera, zeinean sistemaren $S$ entropia maximoa den, beste modu batean interpretatu daiteke.

  • Aintzakotzat hartuko da $f$ puntutik pasatzen den $S$ konstanteko planoa (plano horretan, $S$ entropia da aurreko prozesuko $S^{uni}\equiv S^{sis}$ entropia osoa, oraingo honetan aldatuko ez dena).

  • Plano hori eta $S$ gainazalaren arteko ebakidura kurbako puntuz osatutako prozesua baino ezin da eragin oraingo honetan, horrelako hori baino ez baita bateragarri baldintza esperimentalekin: $S^{sis}=k$.

  • Abiapuntuko oreka-egoera irudiko $i$ egoera izan daiteke. Barne-loturaren bat askatutakoan

  • Baliokidetasunaren esangura fisikoa

• 

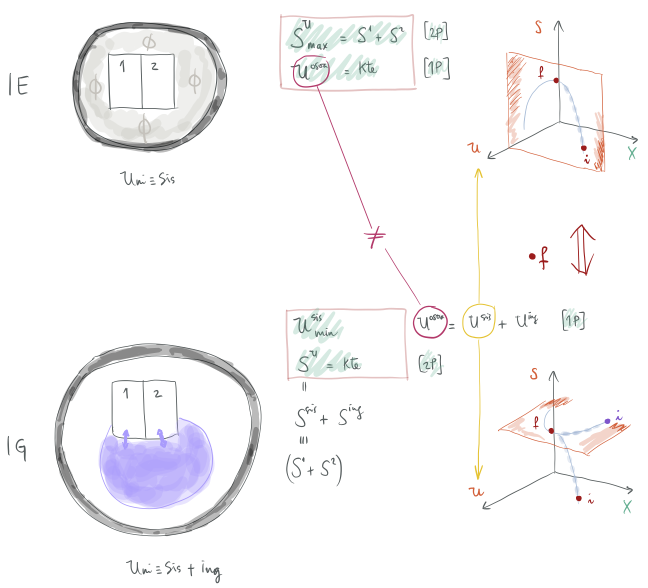
  Baliokidetasunaren esangura fisikoa.

Legendreren Transformazioak

• 8.6 Legendre-ren transformazioak

  • matematikoki, transformazioa

  

  • interpretazioa

  

  • Legendre-ren transformazioak eta aukerako formulazioak

  

  • laburbilduma

  • adierazpen energetikoan:

    • entalpia

    • Helmholtz-en energia askea

    • Gibbs-en energia askea

  • adierazpen entropikoan

previous

Formalismo aldaketa. Oinarrizko ekuazioa

next

Liburua