Ariketak#
Aurkezpena#
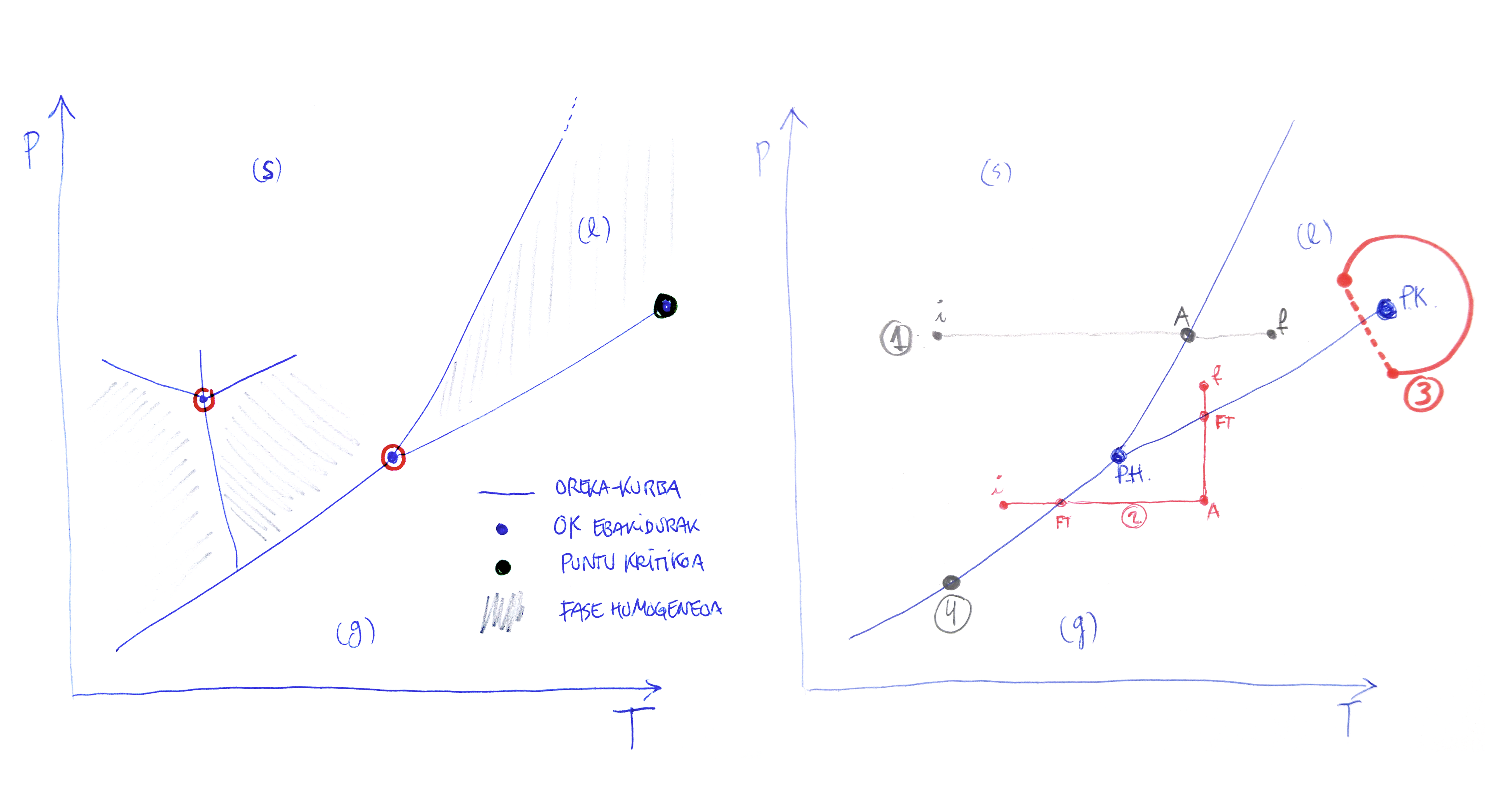
Hurrengo ariketetan fase-diagrametan lan egingo duzu. Izaeran erabat ezberdinak diren lau elementu dituzte:
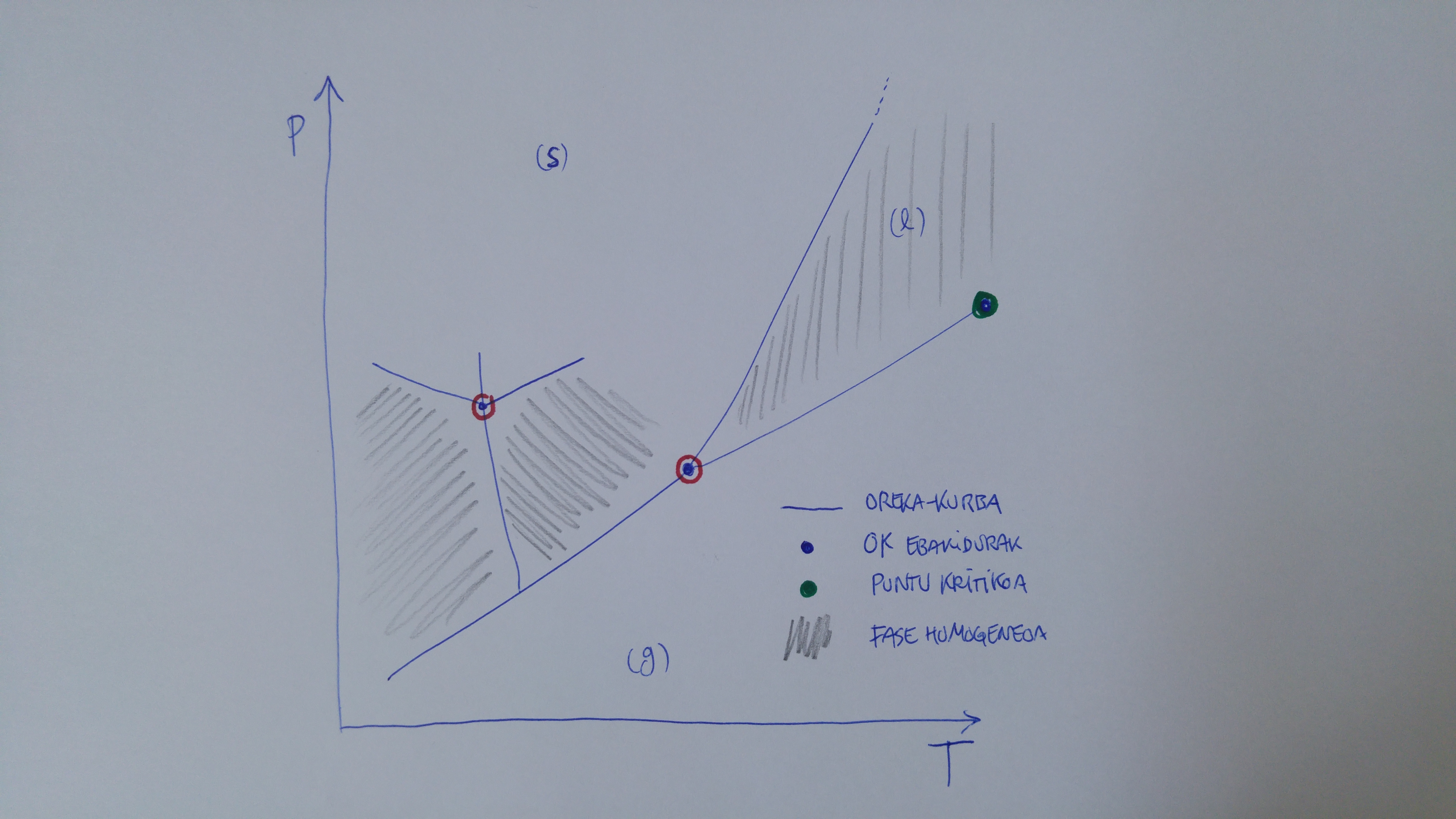
oreka-kurbak: elkarren arteko orekan dauden bi faseren arteko oreka-egoeren segidak.
Urdinez adierazi ditut ezkerreko irudian. Adierazita daude likido/gas, likido/solido, solido/gas eta, solido gunean zenbait oreka-kurba agertzen da; horrek esan nahi du, substantzi hori zenbait fase solidotan ager daitekeela, fase kristalino banatan.oreka-kurben ebakidurak: ebakitzen diren oreka-kurben kopuruaren araberako, baina gutxienez hiru faseren arteko haiek, oreka-egoerak. Gorriz inguratutako puntu urdinez adierazi ditut. Esaterako, puntu hirukoitza. Edo puntu laukoitza, solido gunean, zeinean lau fase (solido) elkarren arteko orekan agertzen diren
puntu kritikoa: likidoa/lurruna (likidoaren eta lurrunaren arteko) oreka-kurbaren muturra. Puntu kritiko bakarra dago honen moduko diagramatan eta beti da likido/gas kurbaren muturra. Ager daiteke fase solidoen arteko oreka-kurbetan, baina inoiz ezin da agertu solido/likido oreka-kurban: kurba horrek ez dauka amaierarik…substantzia desagertu arte, jakina.
fase homogeneo bakarra existitzen den gunea: konfigurazio espazioko, diagramako beraz, aurreko puntuak ez diren guztiek osatzen dituzten guneak. Irudian, pare bat marraztu dut.
Horiek guztiak adierazi ditut beheko ezkerreko irudia. Eskuinekoan adierazi ditut aztertuko dituzun lau prozesu mota.
1 prozesua:Arkatzez marraztutako
Jakina, fase homogeneoetan gertatzen diren prozesuak dira orain arte aztertu dituzun prozesu horien antzekoak, horiek dira, hain zuzen. Kasu honetan, presio konstantekoa: lehenengoa solido fasean gertatzen da eta hirugarrena, gas fasean. Azpiprozesu horiek aztertu behar dituzu orain arte aztertu dituzun moduan; izan ere, orain arteko prozesuetan fase homogeneo bakarrak aztertu dituzu ezer esan gabe, esplizituki esan gabe. Hots, orain arteko prozesuetan
2 prozesua:Gorriz marraztutakoa. Bi azpiprozesuz osatuta dago:
3 prozesua:Gorriz markatutakoa, lerro jarraituaren bidez, eta puntu kritikoa gaindituz, oreka-kurba zeharkatu gabe, oreka-kurbaren alde banatan, eta handik gertu, dauden bi puntu lotzen dituena. Aldi berean aipatutako bi puntuak lotzen duen lerro etena irudikatu dut, oreka-kurba zeharkatzen du berak.
Prozesu hau oso berezia da: honetan ez da lehen ordenako fase-trantsizioa gertatzen, baizik eta bigarren ordenakoa, jarraitua. Horrelako fase-trantsizioetan, aztertu den moduan, Gibbs-en energia askearen lehenengo deribatuak,
Horrek esan nahi du hirugarren prozesuari segituz inoiz ez direla ikusiko aldi berean elkarren arteko orekan bi fase: beti behatuko da fase homogeneo bakarra, zeinaren ezaugarriak era jarraituan aldatuz joango diren. Halako batean, bukaerako oreka-egoeran dagoela sistema, orka-kurbaren beste aldeko puntuan, orduantxe nabarituko dira hasierako eta bukaerako egoeren arteko ezberdintasunak.
Dena dela, posiblea bada deskribatzea kurba hori diagrama horretan eta, gainera, kurba horrek zeharkatzen dituen puntuetan (fisikoki, oreka-egoeretan) ezaguna bada sistemari buruzko oinarrizko ekuazioa, edo gutxienez beharrezkoak diren egoera-ekuazioak, posiblea izango da kalkulatzea prozesuaren ondorioz propietateren batean gertatu den aldaketa:
prozesua:oreka-kurbako puntu baten bidez adierazitako bera: prozesua da fase-trantsizioa bera.
Hurrengo ariketetan oso gomendagarria da beti prozesua irudikatzea diagraman.
irudi-oina#
Proposatutako ariketak#
irudi-oina.#
Testuingurua
1. ARIKETA
Esku artean dugun sistemak 1, 2 eta 3 zenbakiez ezaugarrituko ditugun hiru fase kristalinoetan agertu daiteke.
Puntu hirukoitzaren inguruetan honako hau bete da:
Horietan,
Irudikatu grafikoki faseen oreka-kurbak puntu hirukoitzaren inguruetan,
Hurrengo ariketetan Clausius-en eta Clapeyron-en ekuazioa behin eta berriro erabiliko dugu. Ekuazio horrek osagai bakarreko substantzia baten
Clausius-en eta Clapeyron-en ekuazioaren forma diferentziala honako hau da:
I eta II fase-trantsizioan elkarren arteko orekan agertuko diren bi faseen labelak dira. Beste modu batean ere idatz daiteke ekuazioa: lehen ordenako fase-trantsizioarekin lotutako
Ondorengoetan,
Clausius-en eta Clapeyron-en ekuazioaren forma diferentziala integratu daiteke oreka-kurba bera lortzeko asmotan. Argi dago, integratu ahal izateko esku artean dugun substantziaren egoera-ekuazioa ezagutu behar dugula, areago, bi fase ezberdinetako egoera-ekuazioak. Normalean, hori ez da kasua. Dena dela, era errazean integratu daiteke Clausius-en eta Clapeyron-en ekuazioa, deskribatu nahi den fase-trantsizioan gas-faseak, lurrunak, parte hartuko badu. Orduan, deskribatuko ditugun fase-trantsizioak (oreka-kurbak, hortaz) honakoak izango dira: lurrunketa, likidotik gaserakoa; edo sublimazioa}, solidotik gaserakoa. Hots, fase kondentsatu batetik gas-faserako oreka kurba aztertuko dugu. Horrelako kasuetan, bi dira egiten diren hurbilketak:
Fase kondentsatuekin lotutako bolumen molarra gas-faseari, lurrunari, dagokionarekiko baztertu:
Lurruna gas idealtzat hartu:
Orain, ekuazio diferentziala zuzenean integratu daiteke,
Kontuan izan, aurreko integrazioa
Azkenik, Clausius-en eta Clapeyron-en ekuazioaren bidez presio eta tenperatura jakin batean gertatu den fase-trantsizioa ezagututa, zein beste baldintzatan gertatuko den lortu daiteke; horretan datza bere aplikagarritasuna.
Testuingurua
2. ARIKETA
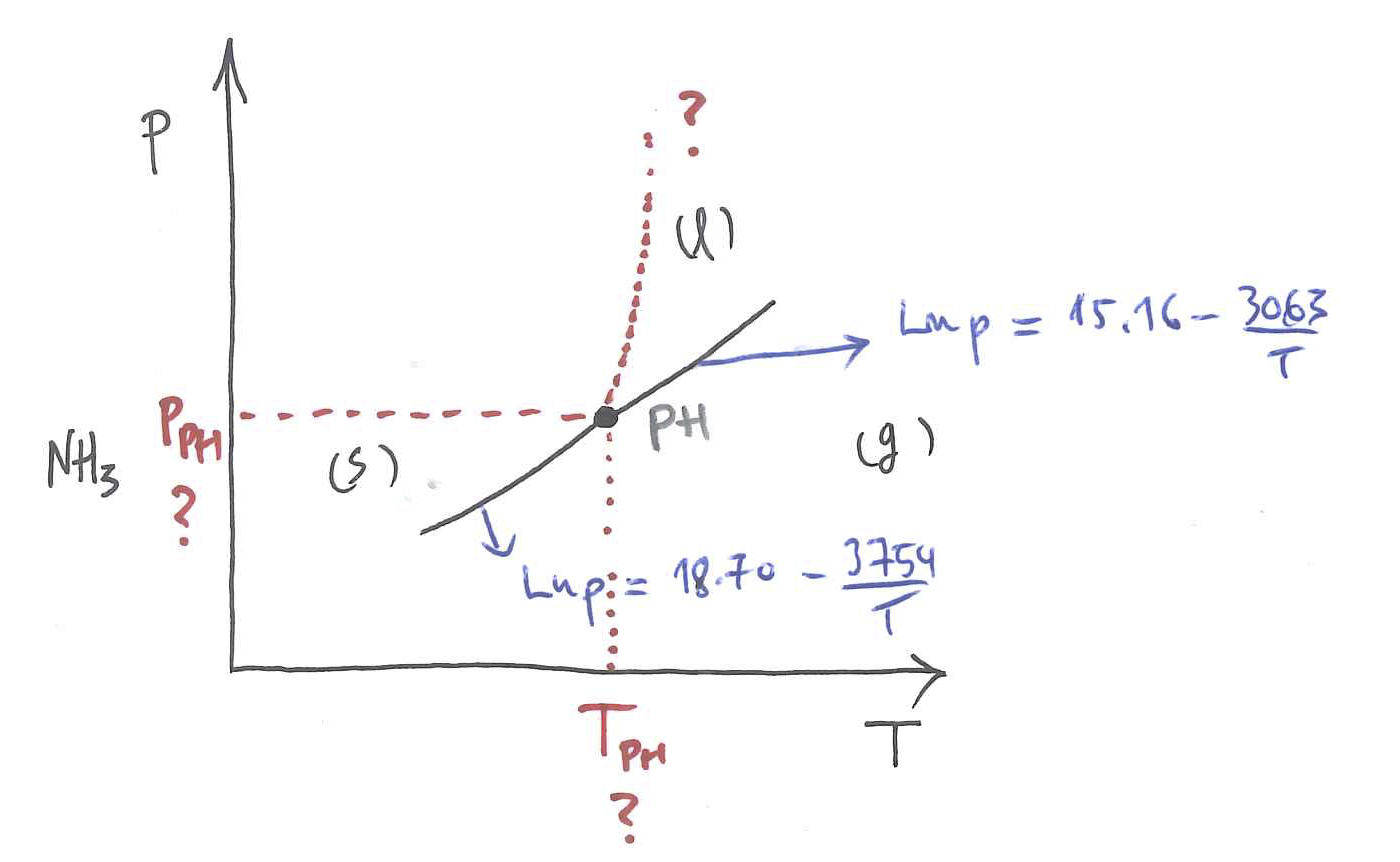
Honako hauek dira amoniakoaren kasuan lurruntzeari eta sublimazioari dagozkien oreka-kurben adierazpenak:
Lortu, kasu bakoitzean, fase-trantsizioari dagokion beroa; hots, lurrunketa-beroa eta sublimazio-beroa.
Lortu, berebat, puntu hirukoitzari dagozkion presioa eta tenperatura.
Testuingurua
3. ARIKETA
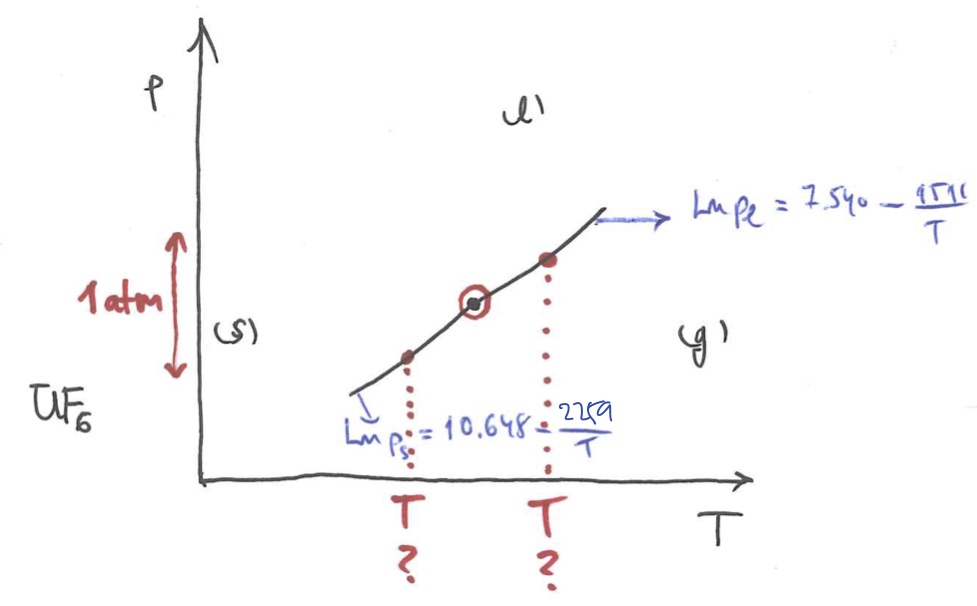
Zer baldintzatan lor daiteke
Presioa 1 atm denean, zer tenperaturatan agertuko du fluoruroak bere lurrunarekiko oreka?
Testuingurua
4. ARIKETA
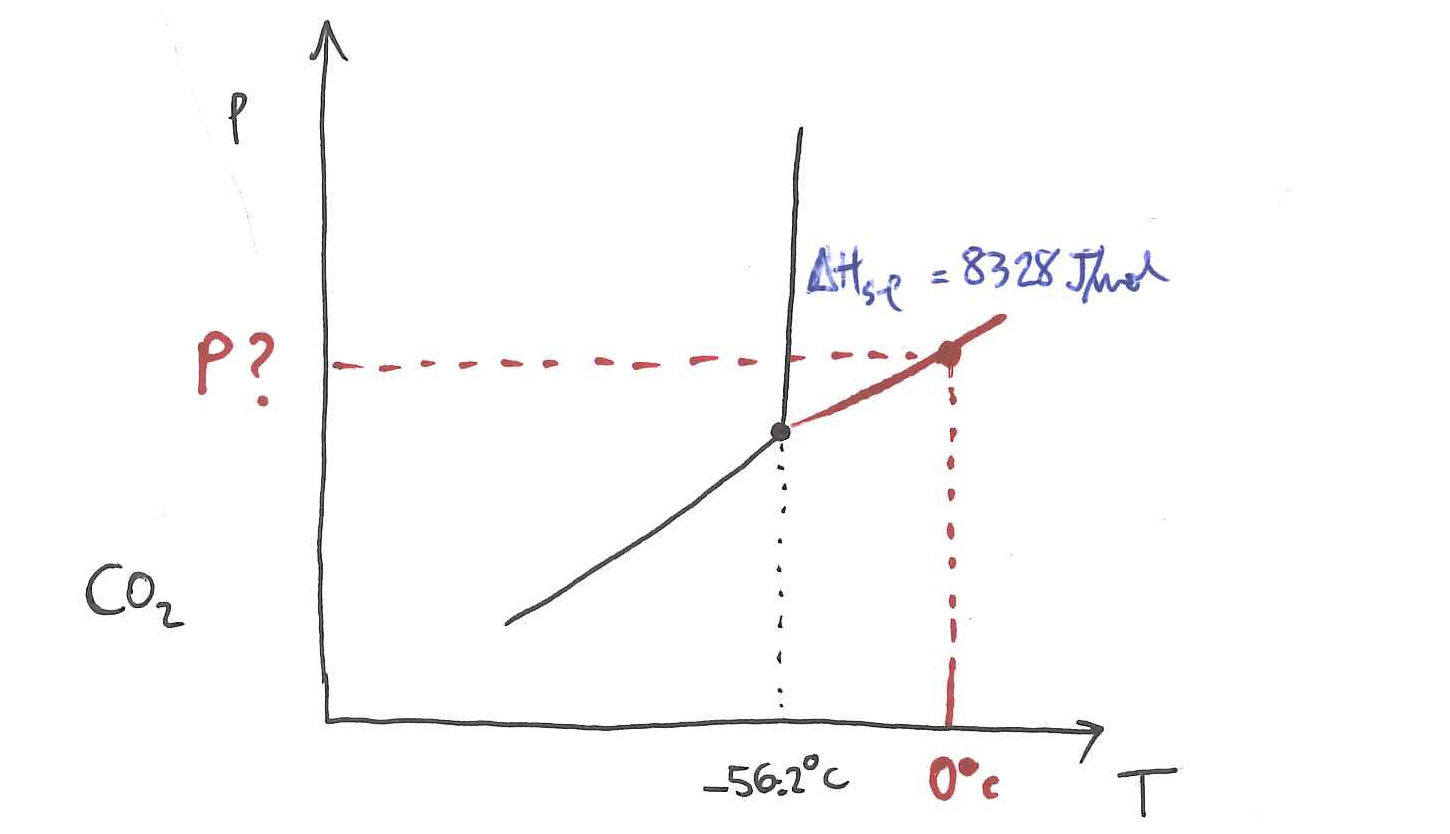
Horretan,
Puntu hirukoitzaren tenperatura -56.2
Lortu
Testuingurua
5. ARIKETA
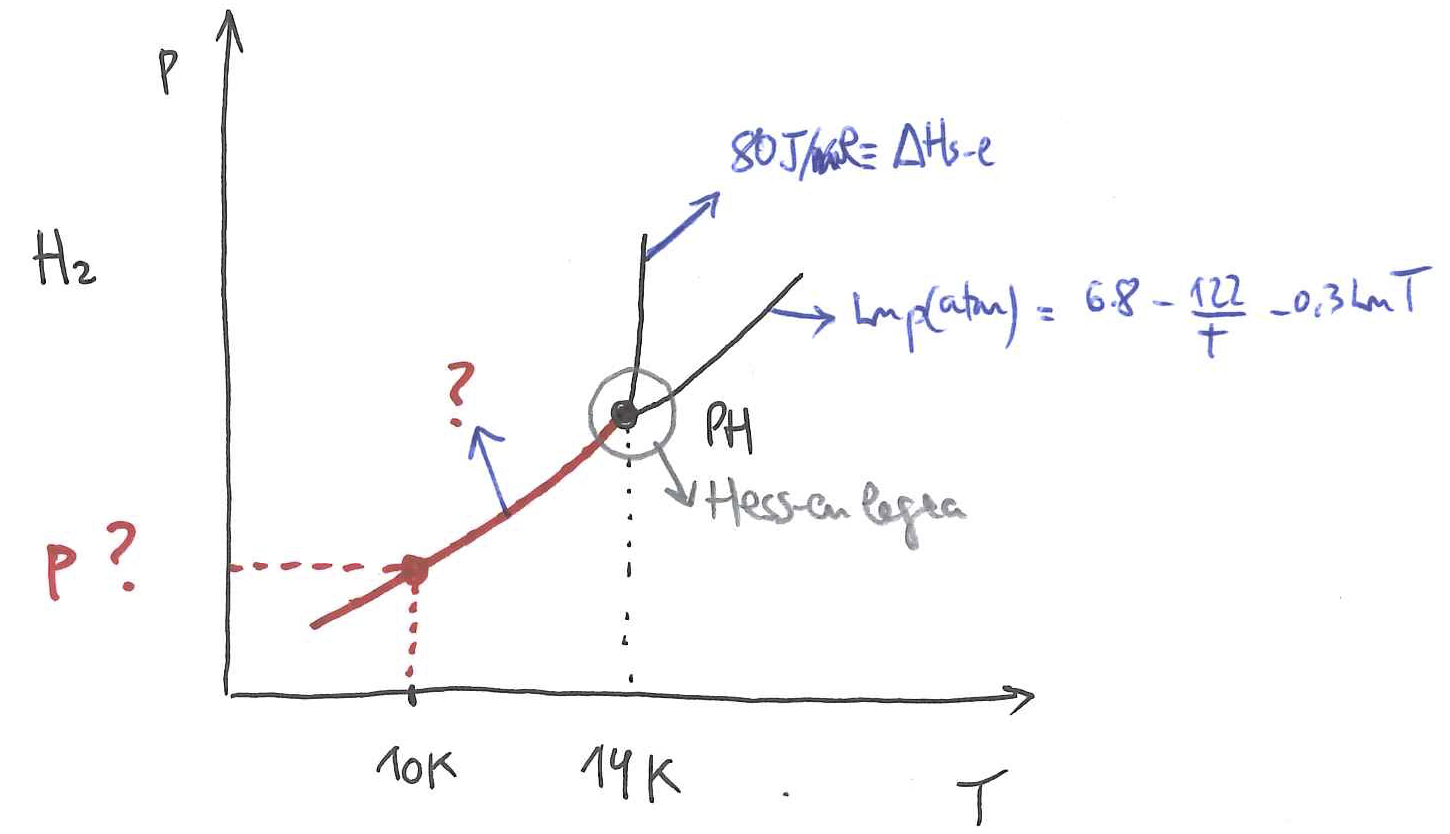
Hidrogenoaren puntu hirukoitzaren tenperatura 14 K da eta, tenperatura berean, hari dagokion fusio-beroa, 80 J/g.
Likidoari dagokion lurrun-presioa honako adierazpen honek eman digu:
Lortu hidrogeno solidoaren lurrun-presioa 10 K-ean.
Laguntza: gogoratu Hess-en legea, zeinaren arabera puntu hirukoitzean agertu daitezkeen fase-trantsizioekin lotutako beroen batura nulua den.
Hau da:
Testuingurua
6. ARIKETA
Esku artean dugun sistemaren kasuan ezaguna da solido/likido oreka-kurbaren malda, puntu hirukoitzean (20 K-ean):
Gainera, puntu horretan, fase solidoaren eta likidoaren arteko bolumen espezifikoen arteko kendura ere ezaguna da (tenperatura-tarte handi batean konstantea dena):
Lortu zer presiotan hasiko den irakiten solidoa, 12 K-eko tenperaturan.
Honako hau da likido/lurruna oreka-kurbaren adierazpena:
Testuingurua
7. ARIKETA
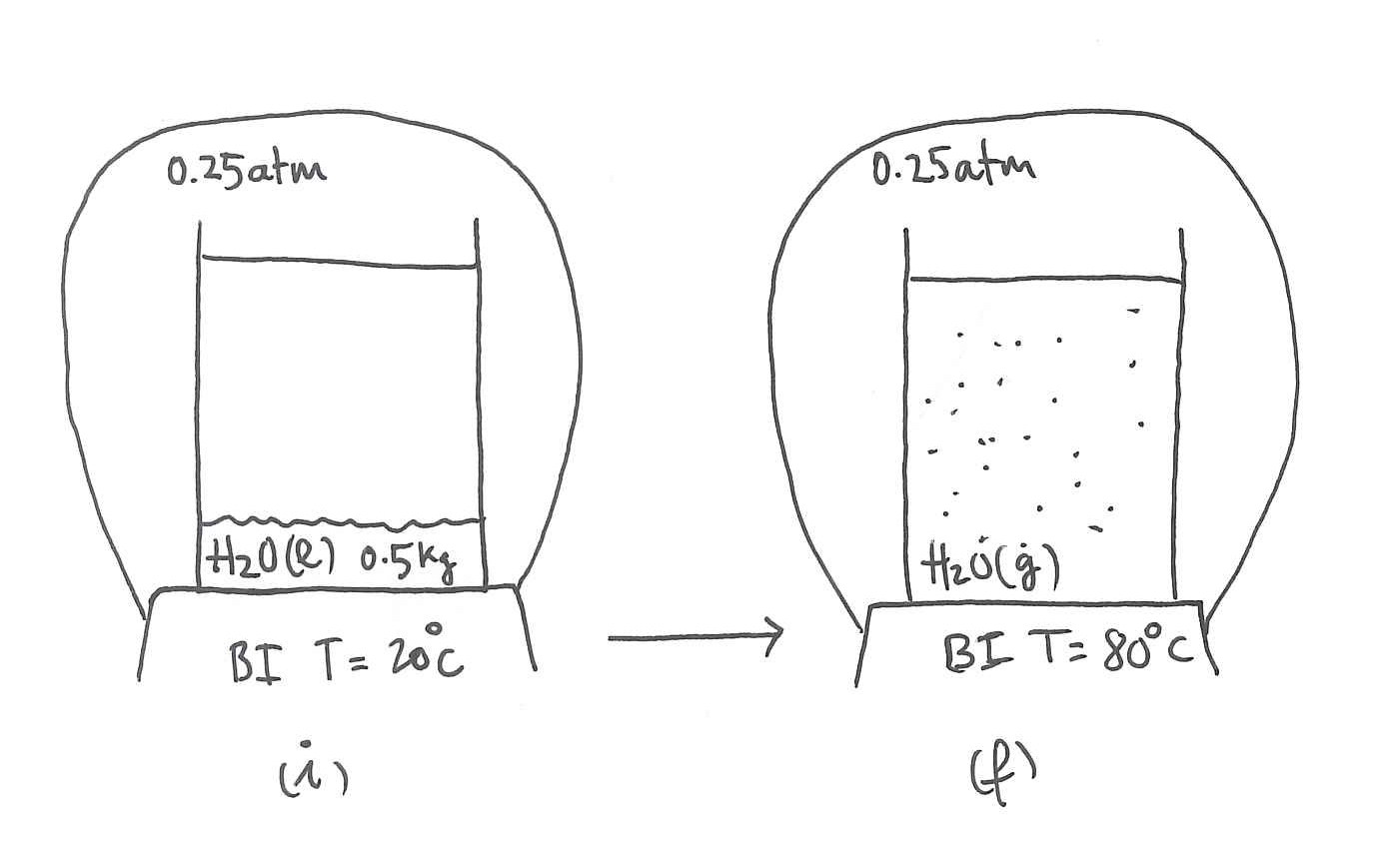
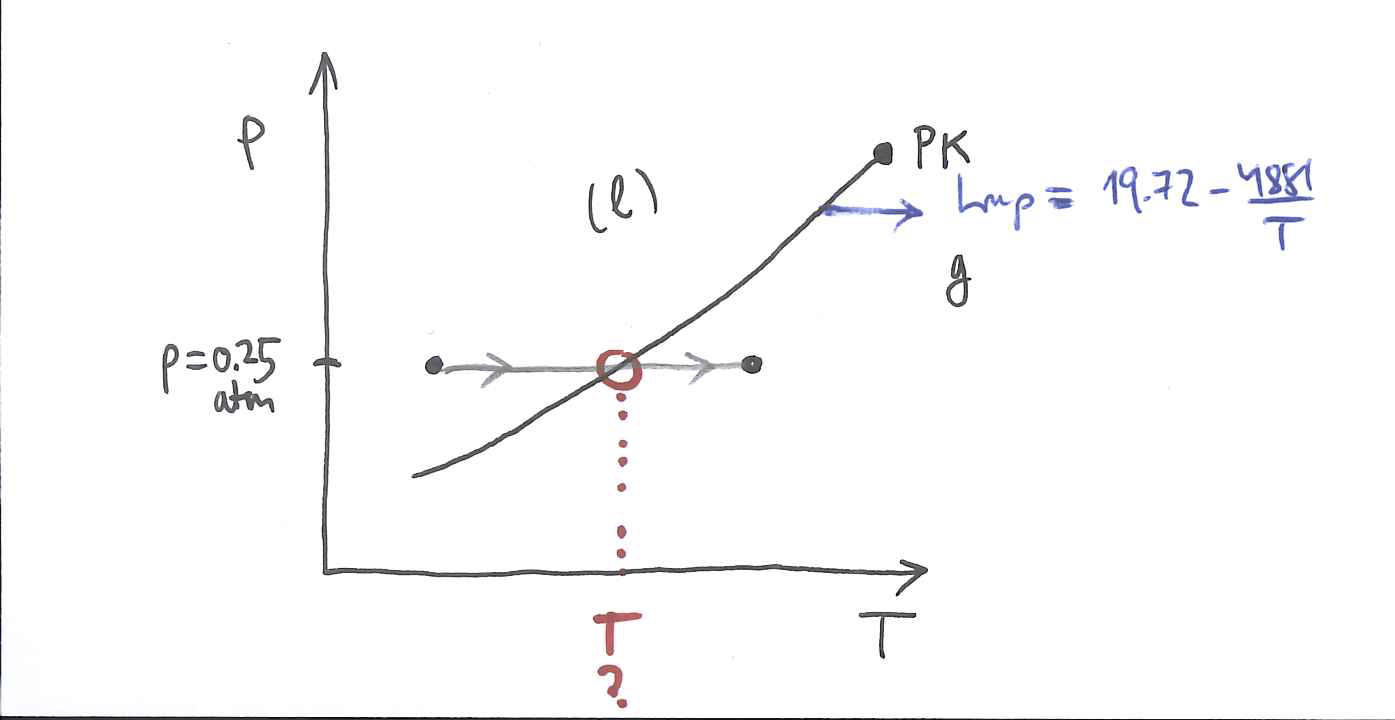
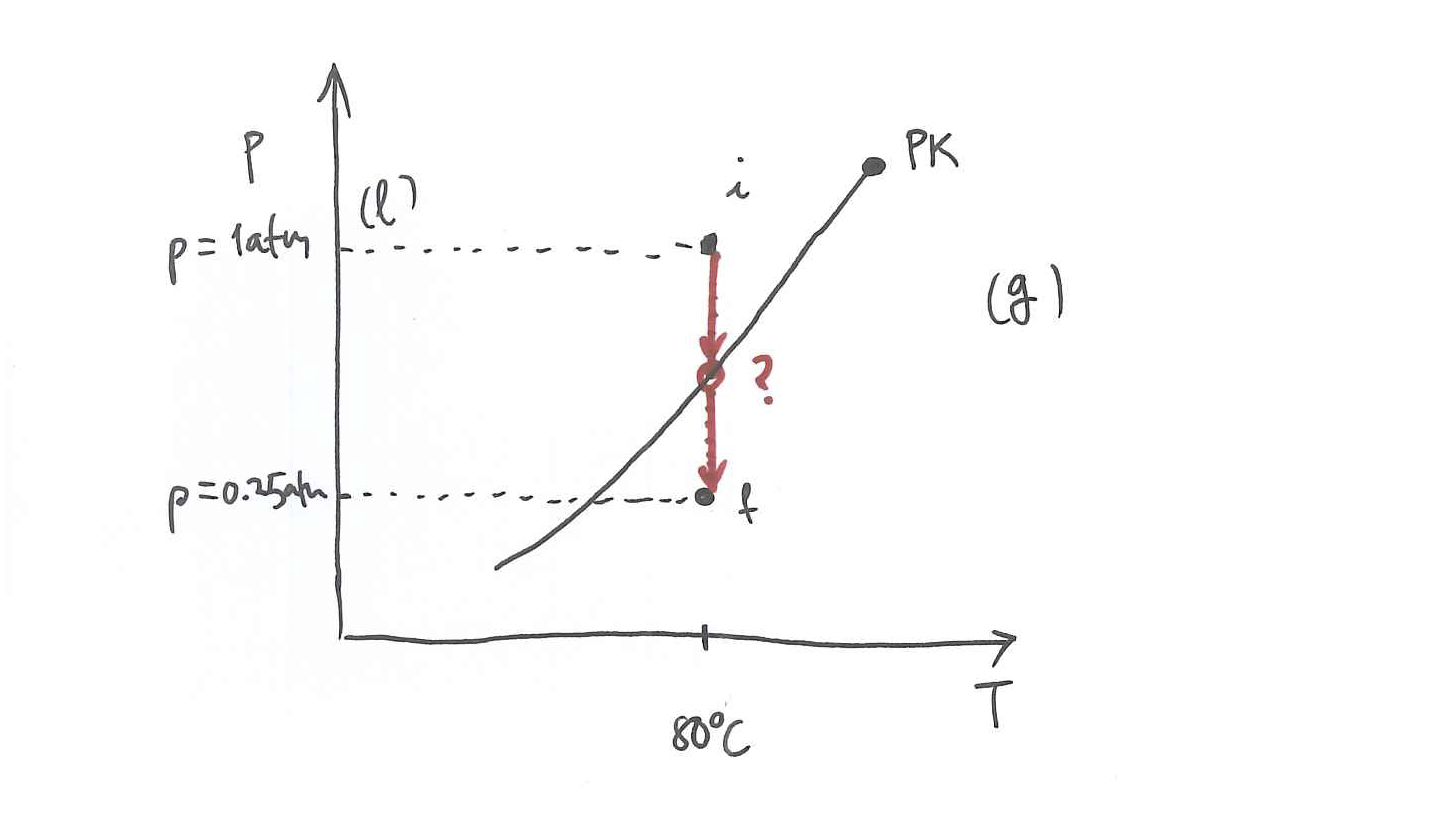
Zilindro batean 500 gr ur likido dago, 0.25 atm eta 20
Lortu uraren eta bero-iturriaren entropia-aldaketak.
Lurruna/likidoa oreka-kurbak ondoko ekuazioari segitu dio:Adierazpen horretan
Uraren bero-ahalmena da 0.3 cal/gK.
Datuak:
Aldez aurretiko iruzkinak:
Irudia ikusi baino lehen, pentsatu, lehenengo, nola egin behar den saiakuntza.
Agian, hoberena da sistema eta ingurunea (irudikatu) identifikatzea eta hasierako egoera grafikoki ezaugarritzea.
Lurruntzearen oreka-kurba emanda dagoenez, seguruena, erabili behar da; hots, eragindako prozesuak fase-trantsizioa eragingo du sisteman.
Komeniko da, beraz, fase-trantsizioaren
Hori guztia egindakoan, ezaugarritu fisikoki sistemaren bukaerako egoera eta adierazi grafikoki,
hasierako eta bukaerako egoerak
prozesua bera
Jakina, bi irudi horiek bateragarri izan behar dute.
Testuingurua
8. ARIKETA
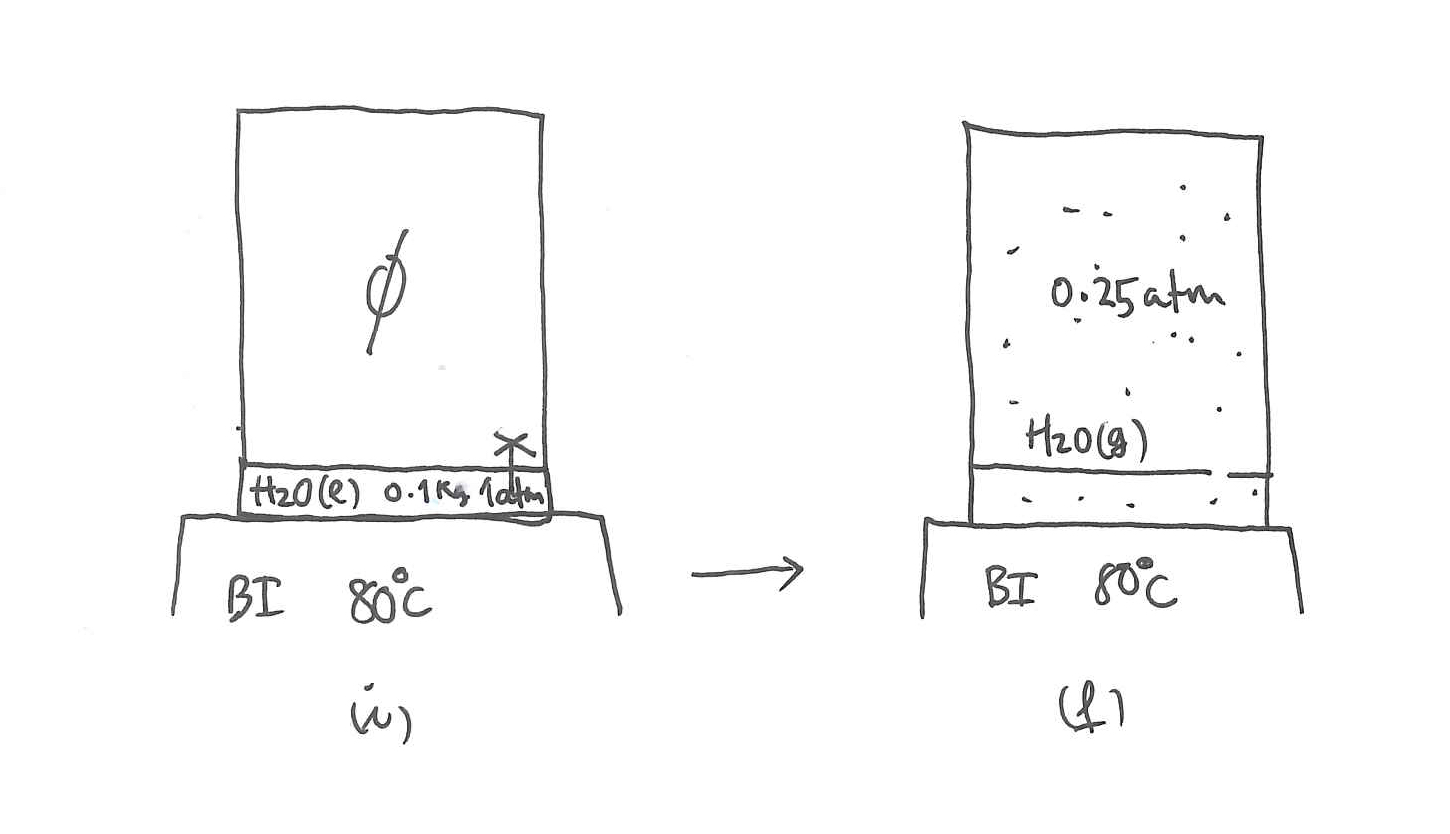
Bero-iturri batekin ukipen termikoan, 80
Irudikatu hasierako eta bukaerako egoerak
Lortu urari dagokion entropia-aldaketa.
Datuak:
Uraren lurrunketaren bero-sorra 540 cal/g da.
Ur likidoaren zabalkuntza-koefizientea
Ur likidoaren presioarekiko bolumen-aldaketa baztergarria da .
Onartu lurruna gas ideala dela eta honako hau
Aldez aurretiko iruzkinak:
Komeni da, kasu honetan ere bai, eragindako saiakuntzaren irudia egitea, ez soilik enuntziatuak eskatzen duen moduan prozesuaren adierazpide grafikoa
Testuingurua
9. ARIKETA
Ur likidoaren entropia molarra 70
Lortu honako hauek:
Ur-lurrunaren entropia molarra 120
Kontuan izan lurrunari dagokion egoera-ekuazioa mekanikoa honako hau dela:Adierazpen horretan
Aipaturiko bi egoeren arteko Gibbs-en funtzioaren aldaketa.
Datuak:
Likidoaren bero-ahalmena:
Lurrunaren bero-ahalmena:
Uraren lurrunketa bero-sorra (
Testuingurua
10. ARIKETA
Aztertu beharreko sistema ondokoa da: 1 atm-ean dagoen gordailuan sartu dugun substantzia baten lurruna.
Gordailua 400 K-ean dagoen bero-iturriarekin ukipen termikoan jarri da eta, tenperatura konstante mantenduz, 10 atm-raino konprimitu dugu.
Ezaguna da substantzia hori
Lurruntze-prozesuaren entropia-aldaketa malda negatiboko lerro zuzena da, honako hau hain zuzen ere:
Substantziaren likidoaren bolumen espezifikoak ondoko egoera-ekuazioari segitu dio:
Irudikatu prozesua
Kalkulatu sistemaren entropia-aldaketa.
Kalkulatu fase-trantsizioan gertatu den barne-energiaren aldaketa.
Puntu hirukoitzaren tenperatura
Azaldu.
Testuingurua
11. ARIKETA
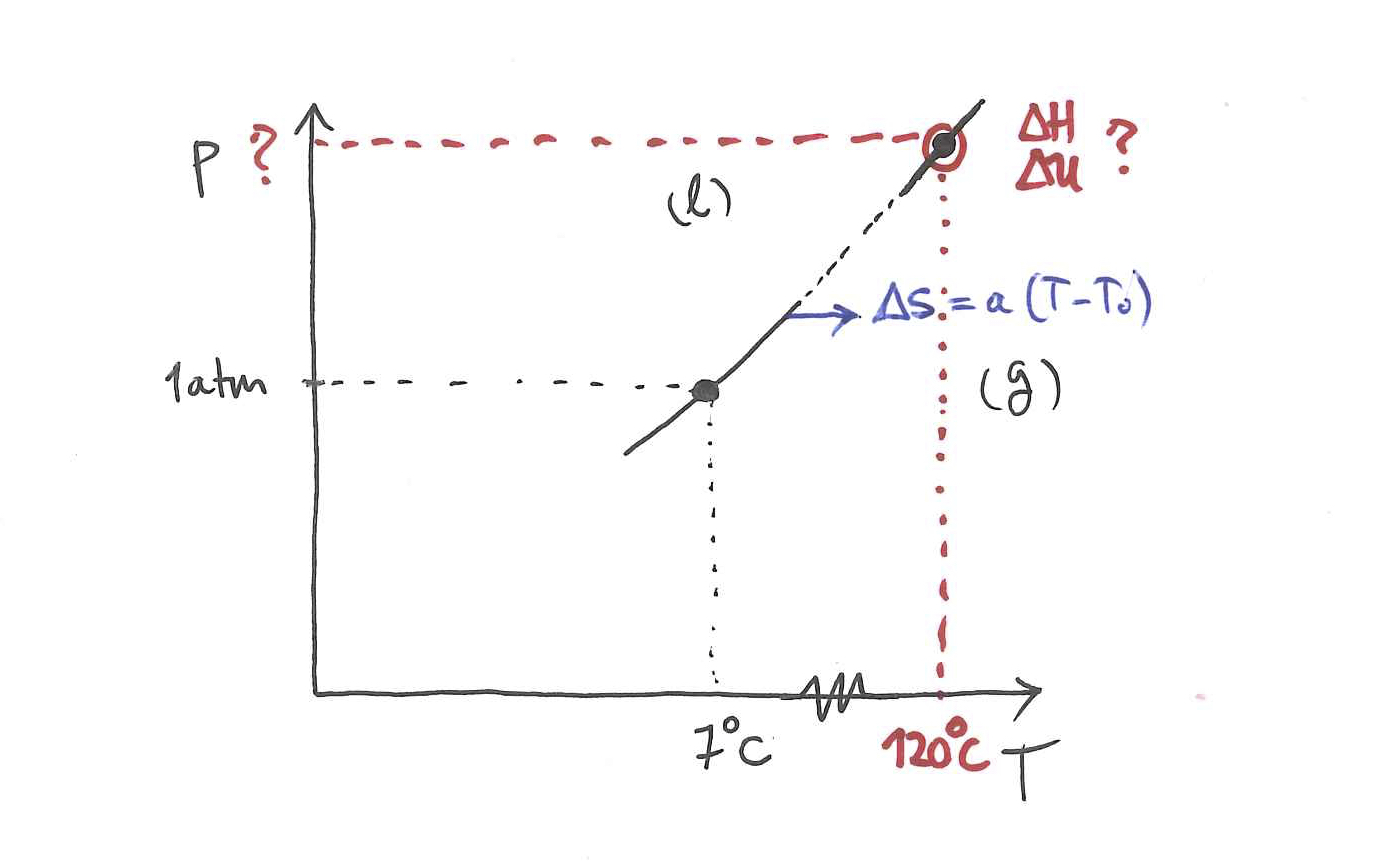
Esku artean dugun sistemari dagokion lurrunketa-tenperatura 7
Fase likidoaren bolumen molarra gas faseari dagokionarekin alderatuz baztergarria dela onartuz eta, gainera, gas fasea gas idealtzat harturik, lortu ondokoak 120
lurrun-presioa,
lurrunketa-entalpia eta
120
irudi-iona#
Testuingurua
12. ARIKETA
Esku artean 30
Lortu zenbat izotz urtuko den.
Lortu sistema osoaren entropia-aldakuntza.
Zer gertatuko litzateke 1 kg ur egon beharrean 2 kg balego?
Datuak:
Ariketa osagarriak#
Testuingurua
13. ARIKETA
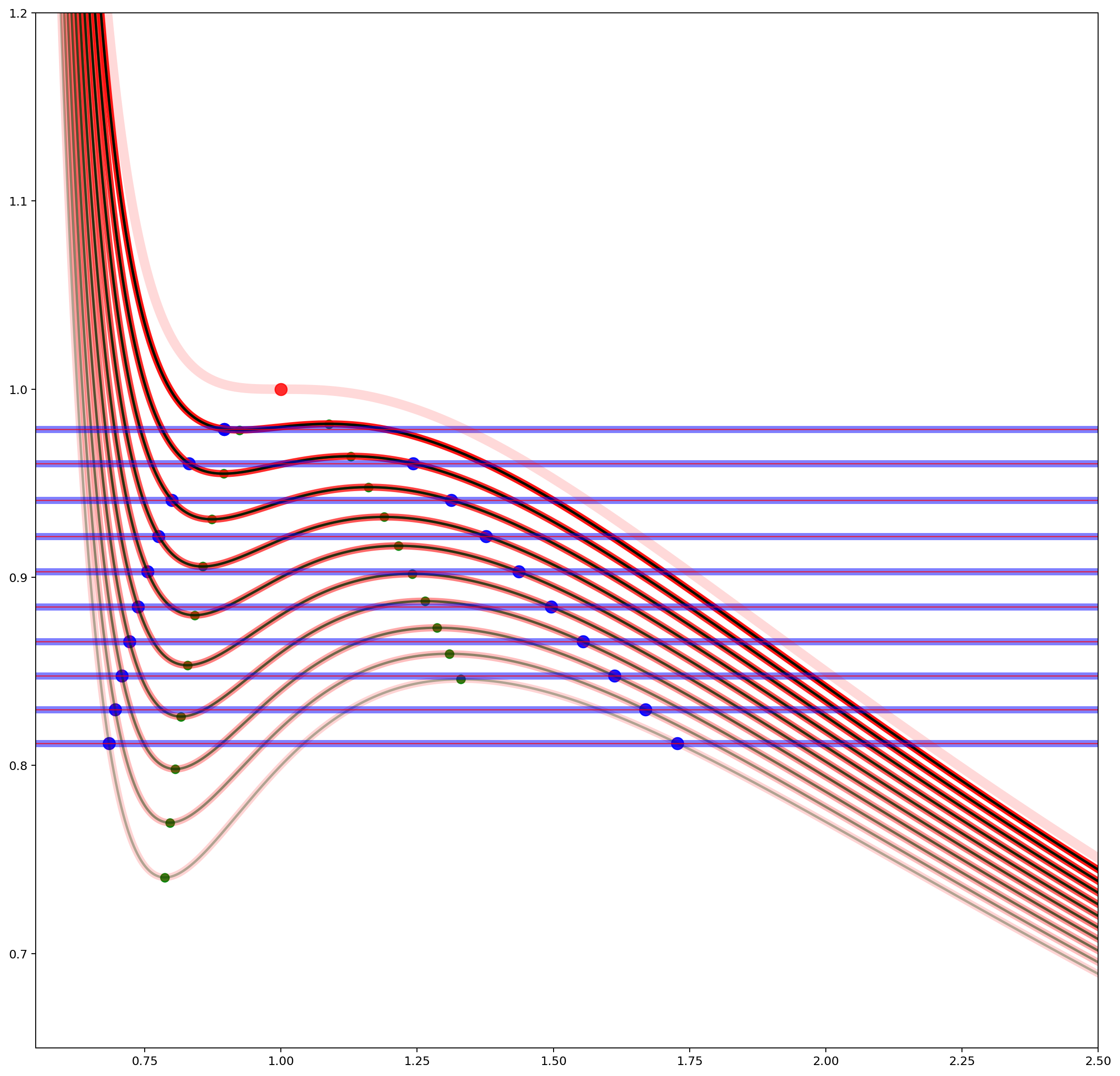
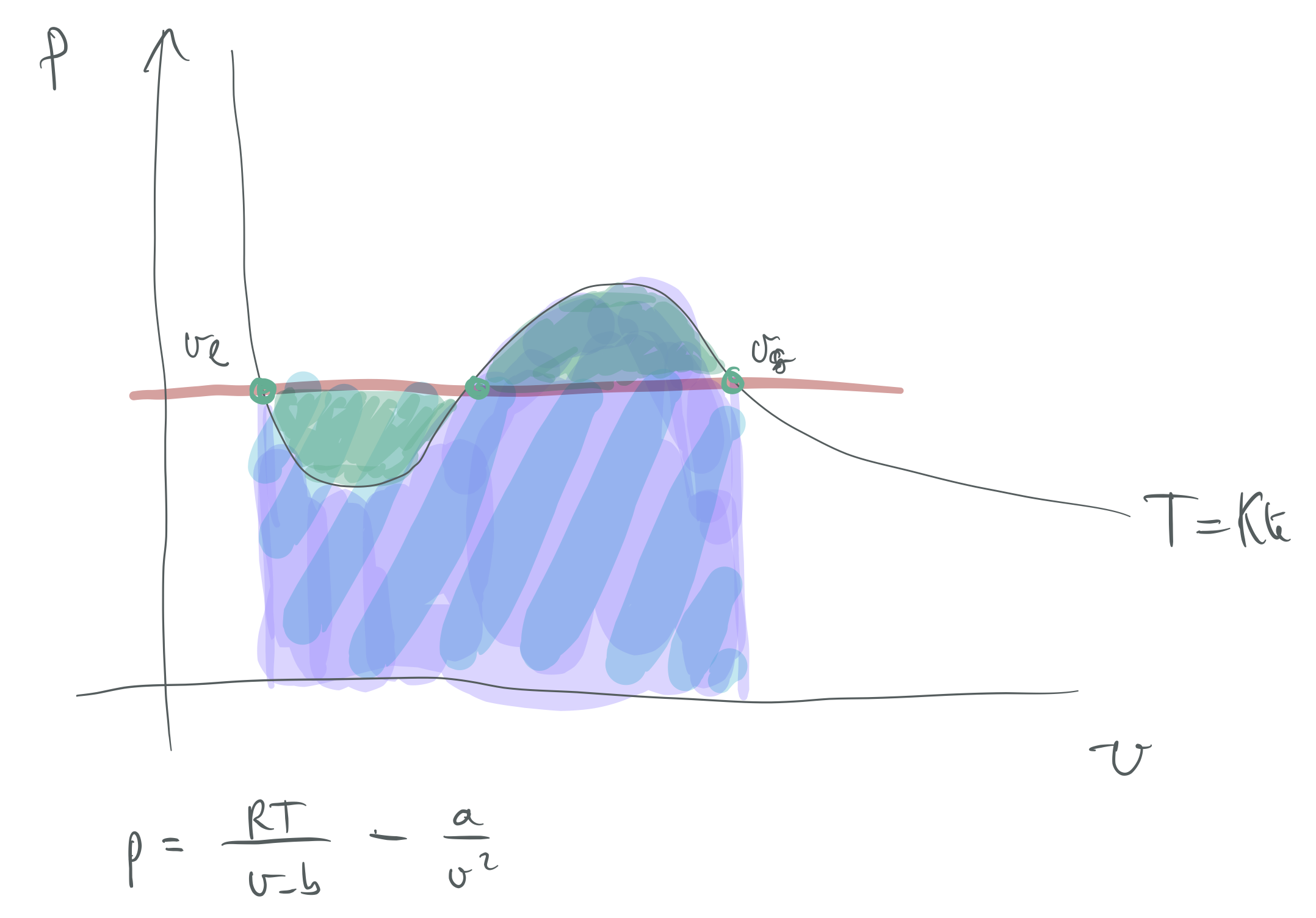
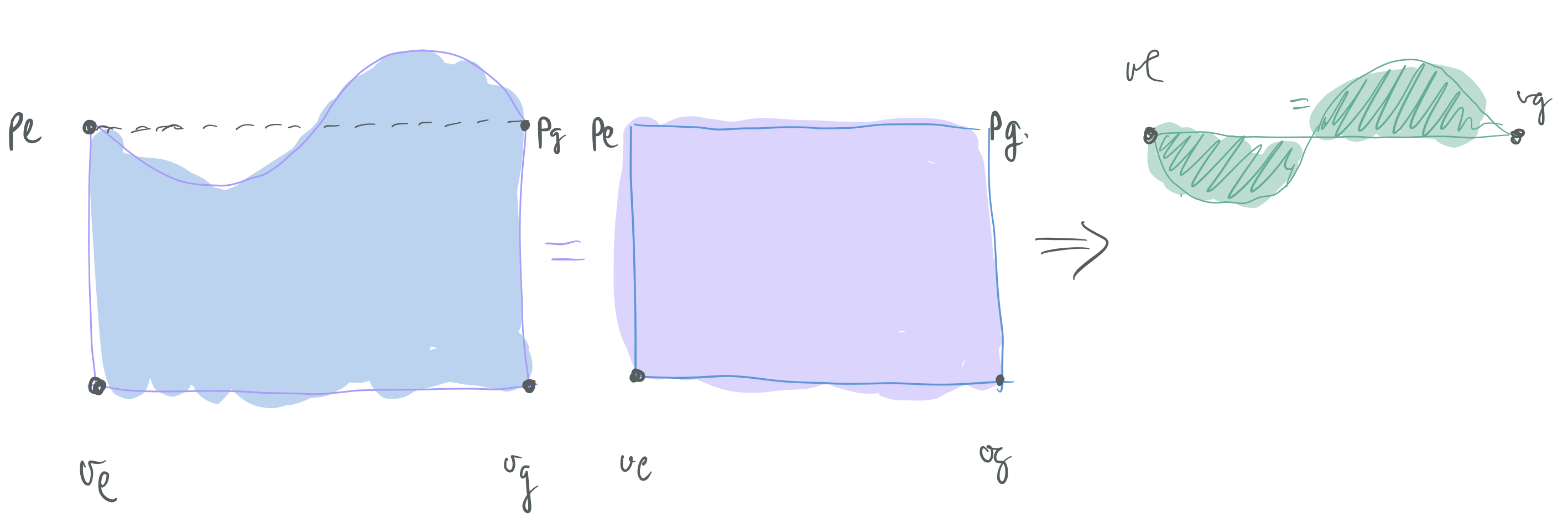
Van der Waals-en egoera-ekuazioa aintzakotzat hartuz, lortu
Testuingurua
14. ARIKETA
Lehen ordenako fase-trantsizioetan, faserik dentsoena oreka-kurbatik gora dago,
Testuingurua
15. ARIKETA
Oreka-kurba bati dagokion adierazpena honako hau da:
Lortu lurruntzearen bero-sorra.
Testuingurua
16. ARIKETA
Ur likidotik ur solidorako fase-trantsizioaren kasuan, lortu
Azaldu zergatik ez den Termodinamikaren Bigarren Printzipioaren aurka egin, aipatutako fase-trantsizioan.
Testuingurua
17. ARIKETA
Lortu
Berebat lortu mol-eko fusio-beroa.
Erabili honako van der Waals-en konstante hauek:
Testuingurua
18. ARIKETA
Aztertu behar da 120
Zenbatekoak dira sistema osoaren presioa eta bolumena?
Erabili ondoko van der Waals-en konstanteak
Testuingurua
19. ARIKETA
Esku artean dugun likidoak, 1000 cal/mol-eko lurruntze-berokoa bera, 127
Zer tenperaturatan hasiko da irakiten presioa 810 mm-ra aldatutakoan?
Testuingurua
20. ARIKETA
Izotzaren fusio-beroa 80 cal/g da 0
Izotzaren eta uraren bolumen espezifikoen arteko erlazioak 1.091 balio du.
Balioztatu nola aldatuko den fusio-puntua, presioa aldatzean.
Testuingurua
21. ARIKETA
Izotzaren fusio-beroa 80 cal/g da, 0
Uraren lurrun-presio asea eta lurruntze-beroa 4.58 mm eta 600 cal/g dira, hurrenez hurren (datu biak 0
Datu horiek abiapuntutzat hartuz, lortu uraren puntu hirukoitzaren tenperaturaren balio hurbildua.
Horretarako, gas-fasean bolumena fase likidoa edo solidoarena baino
Hurrengo bi ariketetan Hidrostatikaren ekuazioa (Ekuazio barometrikoa) erabiliko da:
Demagun aztertu beharreko fluidoa airea dela; gainera gas ideala dela, hots, gas idealaren egoera-ekuazio mekanikoa erabilgarri da eta, orduan, Hidrostatikaren ekuazioan dagoen dentsitatea, tenperatura eta presioaren funtzioan idatz daiteke, honako era honetan:
Testuingurua
22. ARIKETA
Aztertu behar den likidoa 95
Mendixkaren oinarrian dagoenean, berriz, 105
Zenbatekoa da mendixkaren altuera, gutxi gorabehera?
Testuingurua
23. ARIKETA
Lortu uraren irakite-puntua itsas mailatik 2000 m-rako altueran.
Horretarako, ondokoa kontuan hartu beharko duzu: uraren lurruntze-beroa 540 cal/g da, airearen batezbesteko tenperatura 17
Testuingurua
24. ARIKETA
Substantzia baten masa kantitate ezezaguna, 200
Lortu:
Substantziaren bero-ahalmena.
Unibertsoari dagokion entropia-aldaketa, aipatutako prozesua gertatutakoan.
Izotzaren fusio bero-sorra 80 cal/g da.
Testuingurua
25. ARIKETA
Gordailu batean, 1 l-eko bolumenekoa eta hustutakoa bera, 10 g-ko ur kantitatea duen eta 1 atm-ean dagoen kapsula utzi dugu. Gordailua 350 K-ean dago. Kapsula hautsitakoan, uraren zati bat lurrundu da.
Lortu:
Lurrundutako ur kantitatea.
Urari dagokion entropia-aldaketa, aipatutako prozesua gertatutakoan.
Datuak:
Uraren lurrunketa bero-sorra 540 cal/g da; eta uraren zabalkuntza-koefizientea
Baztertu uraren bolumena gordailuaren bolumenarekin alderatzean, eta uraren presioarekiko bolumen-aldaketa.
Testuingurua
26. ARIKETA
Esku artean dugun sistema ondoko hasierako oreka-egoeran dago: (
Gainazal adiabatiko itzulgarrian zeharreko
Prozesuan zehar, ondoko datuak ezagunak dira:
Lortu
Lortu prozesuaren ondoriozko sistemaren
(Oharra: ahaztu unitateak; pentsatu, zenbakiak egokitu direla dena ondo atera dadin.)
Testuingurua
27. ARIKETA
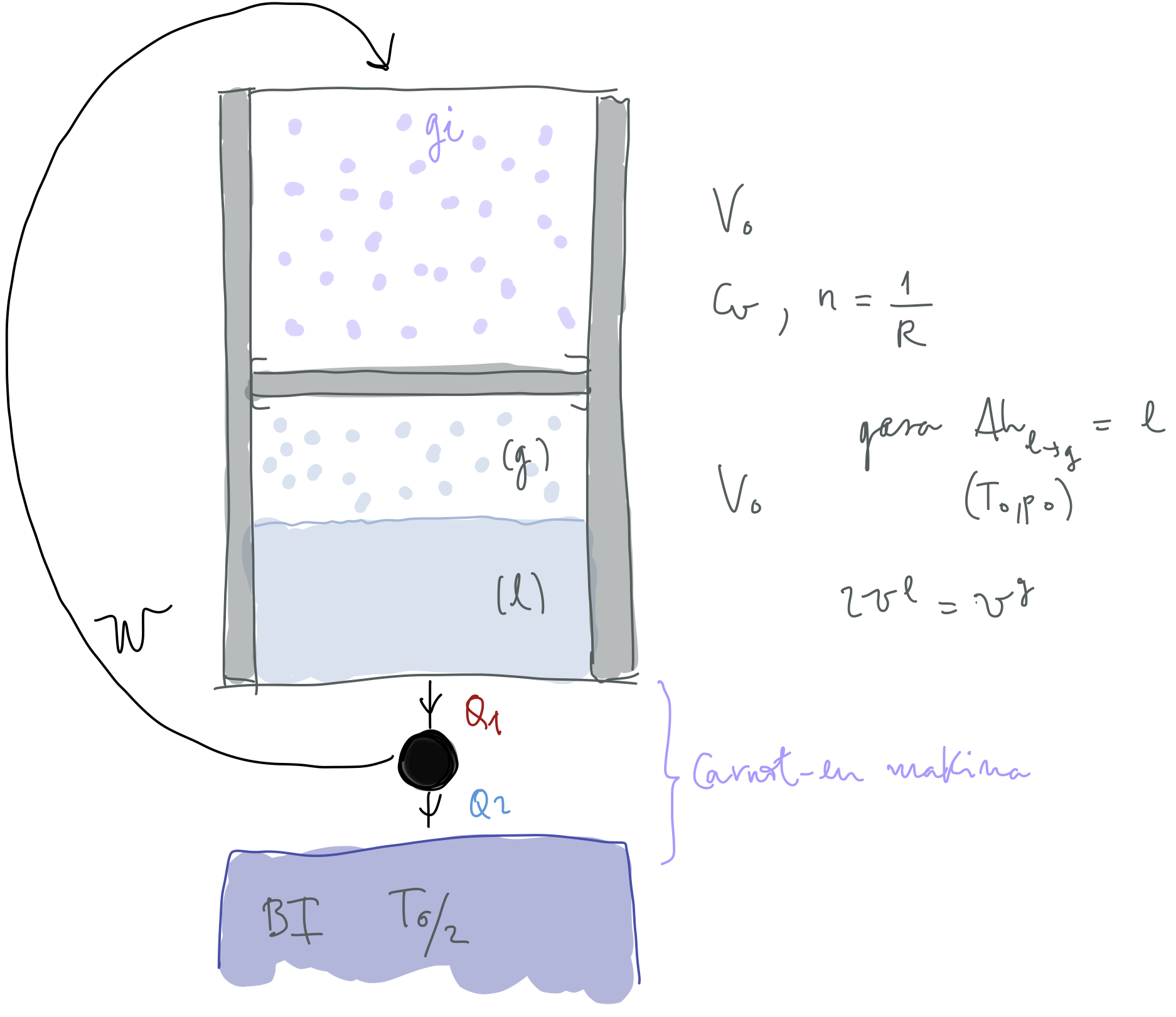
Irudian ageri den zilindroaren alboko hormak adiabatikoak, iragaztezinak eta ez-higikorrak dira, goikoa eta behekoa aldiz, higiezinak, iragaztezinak eta diatermoak. Zilindroaren erdian kokatu den pistoi adiabatikoak, iragaztezinak eta higikorrak
Lor itzazu honako hauek:
gas idealaren bukaerako tenperatura,
bero-iturri hotzari emandako bero kantitatea, eta
gas idealaren eta sistemaren entropia-aldaketak.
Testuingurua
28. ARIKETA
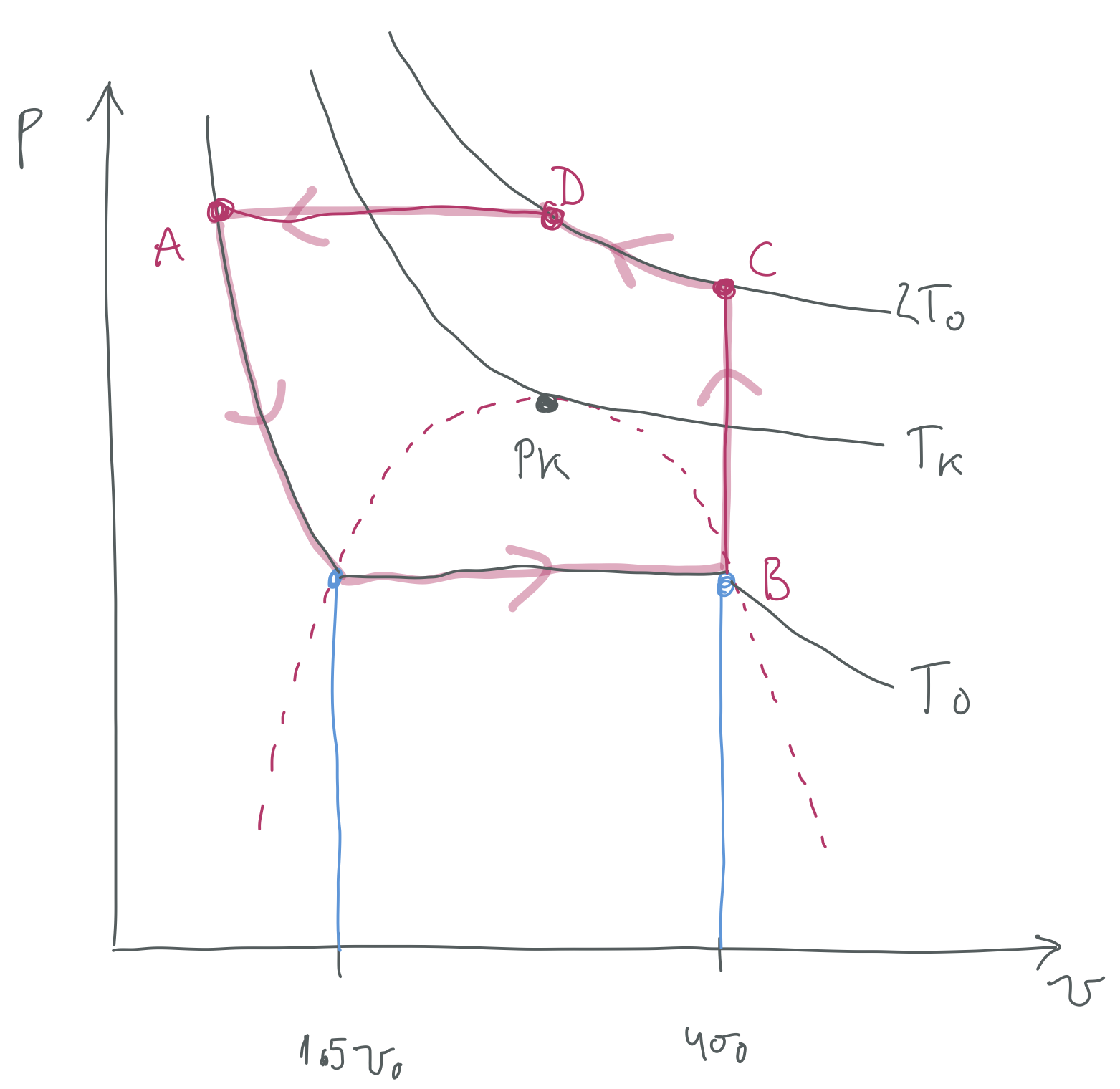
Van der Waalsen egoera-ekuazioa esleitu zaion sistema alboko irudiko diagramako
Lor itzazu honako hauek
Zikloko azpiprozesu guztietan honakoak:
Zein da