Ariketak

Oinarrizko prozesuak, gas ideale(t)an

---

Ondorengo ariketetako helburua da Sistema sinplea gaian aztertutakoak lantzea eta horietaz jabetzea. Kontua da, gauzak egiten joateko, benetako sistema bat beharrezkoa dela. Hortaz, ariketak proposatuta daude gas ideala gaia aztertutakoan. Horrela, sistema jakina izango dugu esku artean, masa konstanteko sistema hidrostatiko jakina, bi askatasun-gradukoa baino ez: mekanikoa eta termikoa. Horiek egoera-ekuazio bana dute lotuta

Honako hau da ariketak ebazteko estrategia:

1. Bildu enuntziatuak sistemari buruz ematen digun informazioa:

   • egoera-ekuazioak

   • koefiziente esperimentalak

   • prozesu bereziekin lotutako informazioa…

2. Bildu sistemaren egoerekin lotutako informazioa:

   • hasierakoa, bukaerakoa, tartekoak…

3. prozesuarekin lotutako informazioa bildu:

   • baldintza esperimentalak

   • aldagairen batek konstante dirauen…

4. Aukeratu deskribapenerako aldagai independenteen sorta

Aldagairen batek konstante badirau, aukeratu aldagai independentetzat. Horrek, prozesuarekin lotutako aldaketa infinitesimalaren adierazpena erraztuko: konstantea den aldagaiaren aldaketa diferentzialak ez du ekarpenik egingo, eta integratu beharreko ekuazioa diferentzialak atal bakarra izango du.

Konbinatu, prozesu jakinaren kasuan, egoera-ekuazioetan dagoen informazioa eta baldintza esperimentalek finkatzen dutena. Hau da:

• egoera-ekuazioak deskribatzen ditu sistemarekin lotuta dauden egoera posible denak.

• Prozesuak aukeratzen ditu posibleak diren horietatik (egoera-ekuazioak deskribatzen dituen horietatik) baldintza esperimental jakinak betetzen dituenak: idatzi informazio hori.

Sistema: gas ideala

Prozesua: $T$ konstantea

Egoera-ekuazio mekanikoa: $pV=nRT$

…baina $T$ konstante denez, $nRT$ ere bai.

Orduan, honako hau izango dugu:

$$pV=konstante$$

• Iruzkinak

1. Gas idealen bero-ahalmenak:

   1. konstanteak dira

   2. Mayer-en erlazio orokortua erabiliz haien kasuan, honako hau da $C_p$ eta $C_V$ bero-ahalmen arteko erlazioa:

      • $C_p-C_V=T{\left({\displaystyle \frac{\partial V}{\partial T}}\right)}_p{\left({\displaystyle \frac{\partial p}{\partial T}}\right)}_V$

      • ${\left({\displaystyle \frac{\partial V}{\partial T}}\right)}_p\equiv {\displaystyle \frac{1}{T}}$

      • ${\left({\displaystyle \frac{\partial V}{\partial p}}\right)}_T\equiv {\displaystyle \frac{1}{p}}$

        $$C_p-C_V=nR$$

      • $C=cnR\Rightarrow C_{p,V}=c_{p,V}nR$

        $$\boxed{{\displaystyle c_p-c_V=1}}$$

   3. • Gas ideal monoatomikoetan: $c_V=\frac{3}{2}$

      • Gas ideal diatomikoetan: $c_V=\frac{5}{2}$

2. Edozein ariketa egiteko, bi motako informazioa erabili behar da:

   1. sistemari buruzkoa:

      1. egoera-ekuazioak, koefiziente esperimentalak…

      2. oreka-egoeraren bat

   2. prozesuari buruzkoa:

      1. kuasiestatiko izan behar du prozesuak
         ez bada, barne-energiaren aldaketa baino ezin da kalkulatu

      2. aipatutako egoeraren bat horrek egon behar du prozesuan

---

Ondoko lau ariketetan oinarrizkoak diren lau prozesu aztertuko dira, gas idealaren kasuan: isotermoa (tenperatura konstantekoa), isobaroa (presio konstantekoa), isokoroa (bolumen konstantekoa) eta adiabatikoa (bero-trukerik gabekoa; ikusiko denez, zenbait kasutan, isoentropikoa).

Enuntziatuetako prozesu guztiak kuasiestatikoak dira (era kuasiestatikoan egin dira); eta, beraz, esku artean dugun sistemari dagozkion egoera-ekuazioak erabilgarriak dira. Egoera-ekuazioak sistemaren oreka-egoerak adierazten ditu; eta prozesua era kuasiestatikoan egiten denean, sistema oreka-egoeretatik pasatzen da. Dena dela, ez da nahastu behar: gauza bat da egoera-ekuazioa, eta beste bat prozesuari dagokion adierazpen matematikoa: azken horretan lehenengoa ordezkatu daiteke; alderantzizkoa ezin da egin.

Masa konstanteko gas idealez osatutako laginari dagokion barne-energiaren adierazpena ondoko hau da: $U=c_{V}nRT+k$; eta, beraz, aldaketari dagokiona beste hau: $\mathrm{\Delta }U=c_{V}nR\mathrm{\Delta }T$. Gas idealaren barne-energiak tenperaturarekiko mendekotasuna baino ez dauka. Aurreko adierazpen hori sistemaren ezaugarria da: barne-energia sistemari dagokion magnitudea da. Ez du, hortaz, prozesuarekin zerikusirik: berdin dio zer modutan, zer baldintza esperimentaletan, gertatu den prozesua. Orduan, ondoko ariketetan, barne-energiaz galdetzen dutenean, aurreko adierazpena erabiliko dugu. Argi dago, prozesuan gertatu den tenperatura-aldaketa ezagutzea nahikoa dela barne-energiaren aldaketa kalkulatzeko; hori izango da bidea.

Gas ideala sistema hidrostatikoa da: sistema bakuna. Beraz, bi ezaugarri baino ez ditu: mekanikoa, ($p,V$) bikoteaz adierazita; eta termikoa, ($T$) aldagaiak adieraziko duena. Lan mekanikoa baino ezin du egin gas idealak, zeinaren adierazpena ondokoa den: $\delta W=-pdV$. Lana diferentzial ez-zehatza da; beraz, dagokion balioa lortzeko, prozesua ezagutu behar da: prozesuak definituta egon behar du. Hots, prozesuari dagokion $p=p(V)$ adierazpen matematikoak ezaguna izan behar du. Hori ezagututa, aurreko adierazpenean ordezkatu; eta integratu egin behar da. Puntu horretan, sistemaren egoera-ekuazioa erabil daiteke. Hori guztia da ondokoetan egingo duguna: lehenengo egoera-ekuazioa erabili $p=p(V)$ lortzeko; ondoren, prozesua definitu duten baldintza esperimentalak kontuan hartuko ditugu, aurreko integrala kalkulatzeko. Ondoko kasu guztietan, lanaren adierazpen diferentziala honakoa da: $\delta W=-\frac{nRT}{V}dV$. Horretan aplikatuko ditugu baldintza esperimentalak.

Azkenik Termodinamikaren Lehenengo Printzipioa aplikatuko dugu prozesuetan trukatu den beroa lortzeko: $Q=\mathrm{\Delta }U-W$. Zenbait kasutan, errazagoa gerta daiteke aurreko ordena aldatzea.

---

Testuingurua

1. ARIKETA

Bereizte-horma diatermoz inguraturiko gas ideala dugu esku artean; $T_0$ tenperaturako bero-iturriarekin ukipenean eta, berebat, hasierako $p_i$ presioko presio-iturriarekin ukipenean. Presio-iturriaren presioa $p_f$ balioraino kuasiestatikoki aldatu da. Lortu honako hauek:

• egindako lana,

• trukaturiko beroa

• gasaren barne-energiaren aldaketa.

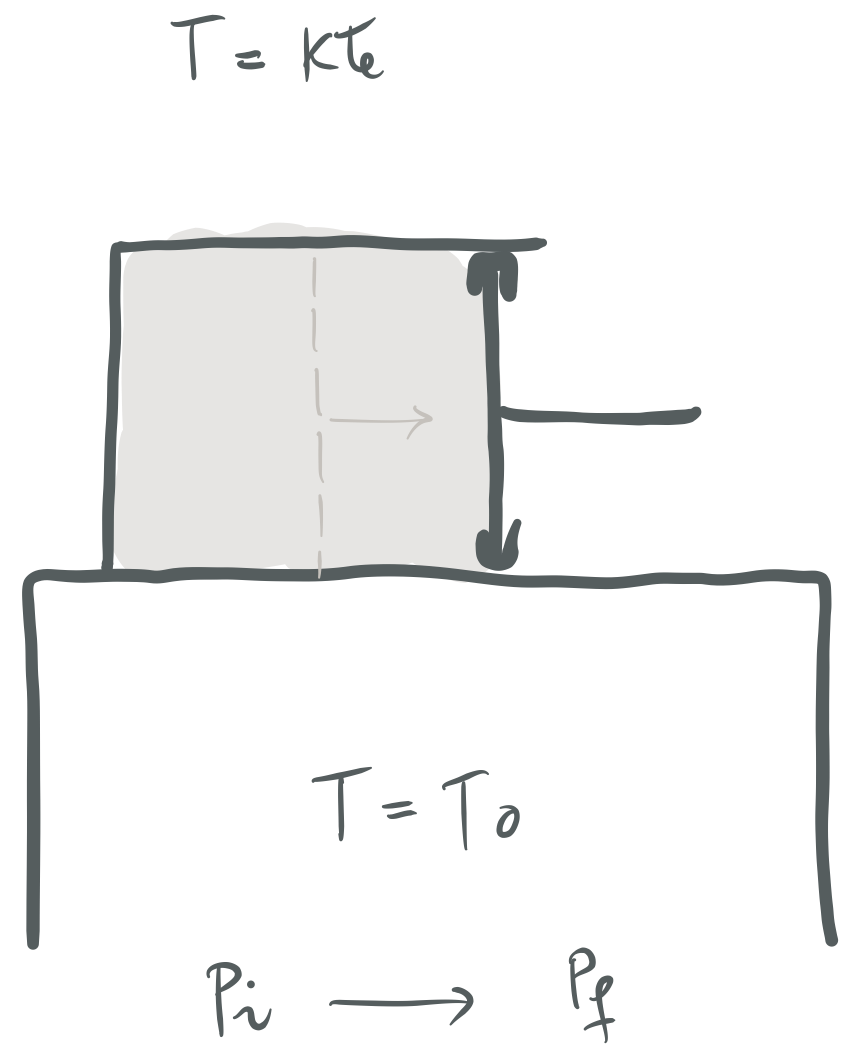
Prozesu isotermoa fisikoki aurrera eramateko eratu daitekeenaren adierazpide grafikoa.

Emaitza

Ebazpen posible bat…

Erantzunen ordena aldatuko dut.

• Bero-iturriarekin ukipenean gertatzen den prozesuan tenperatura konstantea da; prozesu isotermoa da, beraz.

$$\begin{array}{r}\begin{array}{l}\mathrm{\Delta }U=c_{V}nR\mathrm{\Delta }T\\ \mathrm{\Delta }T=0\end{array}\}\Rightarrow \boxed{{\displaystyle \mathrm{\Delta }U=0}}\end{array}$$

• Tenperatura konstantea denez, prozesuaren ibilbidea finkatuta dago eta lana, esaterako (diferentzial ez-zehatza) kalkulatu daiteke, ibilbidean integratuz. Kalkulatuko dut lana. Horretarako, $p=p(T,V)$ funtzioa, prozesuarena, adieraziko dut.

$$W=-\int \frac{nRT}{V}dV$$

• eta tenperatura konstantea denez:

$$W=-\int nRT\frac{1}{V}dV$$

$$\boxed{{\displaystyle W=-nRT\ln \frac{V_f}{V_i}}}$$

• edo, egoera-ekuazioa erabilita:

$$W=-nRT\ln \frac{p_i}{p_f}$$

• Azkenik, beroa kalkulatzeko, prozesu osoari, makroskopikoari, lehen printzipioa aplikatuko diot, diferentziaz kalkulatu daitekeela esaten da:

$$\boxed{{\displaystyle Q=-W}}$$

Interpretatu dezadan aurreko emaitza. Bero-iturriarekin ukipen termikoan gertatu den prozesua denez, tenperatura konstantea da. Ondorioz, gas idealaren barne-energiaren edukia ezin da aldatu: hasierakoa bukaerakoaren berdina da. Baina, gas ideala zabalduko da, kuasiestatikoki eta, beraz, ingurunearekin lotura mekanikoa duela; hau da, lana egin du, kanporatu du, kasu honetan. Horrek energiaren edukia beheratuko du. Bero-iturritiko bero-xurgapenak konpentsatuko du beherapena. Barne-energiaren edukia aldatu gabe lana egin ahal izateko beroa xurgatu behar du bero-iturritik. Beroa lan bihurtuko da, sistema tartekari moduan erabilita.

---

Testuingurua

2. ARIKETA

Pistoi batek, $M$ masakoa eta $s$ sekzioko horma diatermo eta iragaztezinezko zilindro bertikal batean dagoena bera, 1 mol gas itxi du. Bero-iturrien segida infinituarekin ukipenean jarriz, $T_1$-etik $T_2$-ra pasarazi da gasaren tenperatura. Lortu honako hauek:

• Hasierako eta amaierako egoeren presioa eta bolumena,

• $Q$, $W$ eta $\mathrm{\Delta }U$.

Kontuan izan honako hauek: $C_V$ eta $C_p$ konstanteak direla, pistoiaren beste aldean hutsa dagoela eta, azkenik, grabitateak soilik duela eragina pistoiaren gainean.

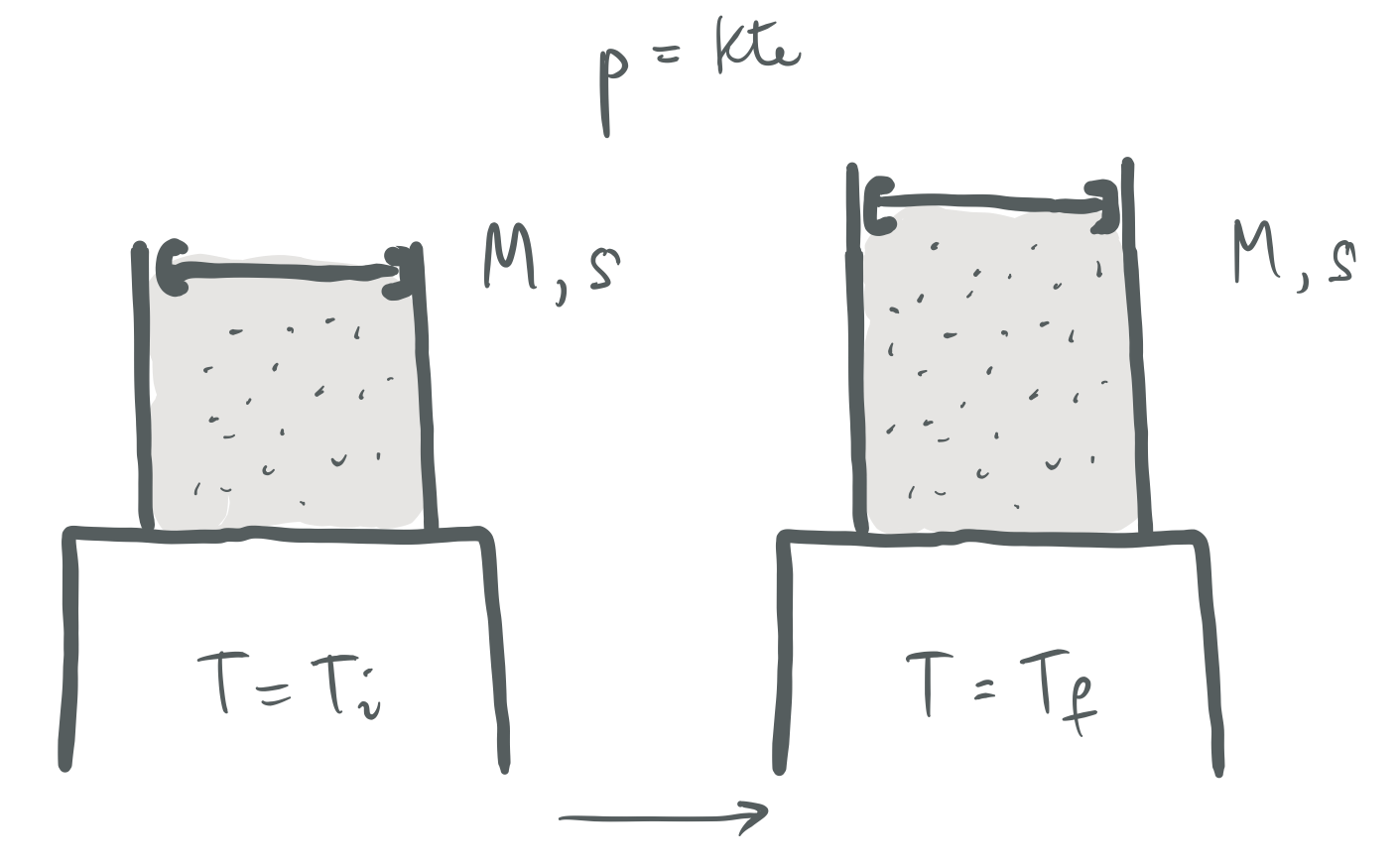
Prozesu isobaroa fisikoki aurrera eramateko eratu daitekeenaren adierazpide grafikoa.

Emaitza

Ebazpen posible bat…

Tenperatura era kuasiestatikoan aldatzeko, bero-iturrien sorta batekin ukipen termikoan jarri behar da sistema. Kasu honetan, presio konstantea eragingo duen pistoia dago zilindroa ixten; beraz, gertatuko den prozesua presio konstantekoa da, isobaroa $p=\frac{Mg}{s}$, esan bezala. Tenperaturak gora egiten duen heinean, presioa konstantea denez, bolumenak ere bai gora egingo du: proportzionalak dira bolumena eta tenperatura (egoera-ekuazio mekanikoa), presioa konstante denean.

1. Bolumena kalkulatzeko egoera-ekuazioa erabiliko da: $pV=nRT\Rightarrow V=\frac{nRT}{p}$

$$pV=nRT\Rightarrow V=\frac{nRT}{p}\Rightarrow V_f=\frac{nR{T}_f}{p}\Rightarrow \boxed{{\displaystyle V_f=\frac{s}{Mg}nR{T}_f}}$$

2. Barne-energia kalkulatzeko, egoera-funtzioa denez (diferentzial zehatza), berdin dio nolakoa izan den prozesua, zer ibilbidetan gertatu den. Egoera-ekuazio termikoaren bidez lor daiteke beti barne-energiaren aldaketa.

$$\mathrm{\Delta }U=c_{V}nR\mathrm{\Delta }T\Rightarrow \boxed{{\displaystyle \mathrm{\Delta }U=c_{V}nR(T_f-T_i)}}$$

3. Lanari dagokionez, kontuan hartuko dut prozesua isobaroa izan dela:

$$W=-\int pdV\Rightarrow W=-p\int dV\Rightarrow W=-p\mathrm{\Delta }V\Rightarrow$$

$$W=-\frac{Mg}{s}\frac{s}{Mg}nR(T_f-T_i)\Rightarrow \boxed{{\displaystyle W=-nR(T_f-T_i)}}$$

4. Beroa kalkulatzeko, berriro ere bai diferentziaz egin daiteke:

$$Q=c_{V}nR(T_f-T_i)-\{-nR(T_f-T_i)\}\Rightarrow Q=(c_V+1)nR(T_f-T_i)\Rightarrow \boxed{{\displaystyle Q=c_{p}nR(T_f-T_i)}}$$

• Konturatu behar da, zuzenean kalkulatu daitekeela, kasu honetan, gas idealak trukatu duen beroa, ezaguna baita nola gertatu den prozesua, presio konstantean. Orduan, koefiziente esperimentalaren definiziotik abiatuta lor daiteke, kasu honetan, presio konstanteko bero-ahalmena.

• Azken adierazpena idazteko gas idealaren Mayer-en erlazioa erabili dut: $c_p=c_V+1$. Edo: $C_p=C_V+nR$.

---

Testuingurua

3. ARIKETA

Aurreko ariketako sistema berbera dugu; beraz, gas ideala dugu esku artean. Kasu honetan, ordea, bolumena konstante mantenduko dugu. Horretarako, pistoiaren gainean area era jarraituan botako dugu. Lortu:

• Botatako are kantitatea,

• $Q$, $W$ eta $\mathrm{\Delta }U$.

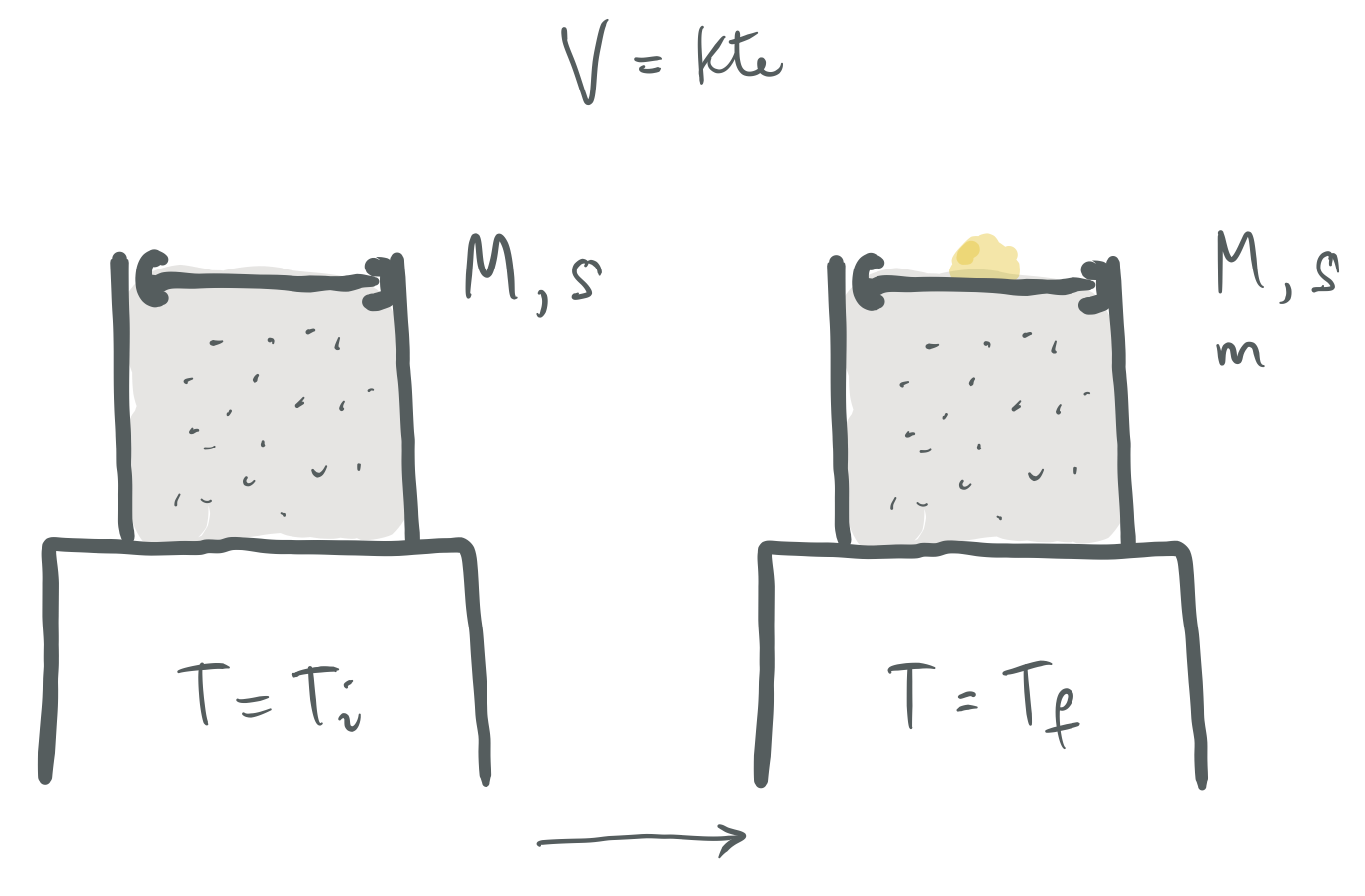
Prozesu isokoroa fisikoki aurrera eramateko eratu daitekeenaren adierazpide grafikoa.

Emaitza

Ebazpen posible bat…

Oraingo honetan, berriro ere bai, bero-iturrien sorta erabiliz, sistemaren tenperatura aldatuko da $T_1$etik $T_2$ra; baina, bolumena konstante mantenduz. Tenperatura-aldaketak berarekin lotuta dakarren bolumen-aldaketa (presioa konstante mantenduz), presioa aldatuz konpentsatuko dugu. Kasu honetan, presioak segituko dio tenperaturari: $pV=nRT\Rightarrow p\propto T$, $\frac{nRT}{V}$ konstantea baita.

$$\begin{array}{r}\begin{array}{l}\begin{array}{c}{V}_i=V_f=V\\ \begin{array}{l}{p}_i=\frac{nR{T}_i}{V}\\ p_f=\frac{nR{T}_f}{V}\end{array}\end{array}\}\Rightarrow \mathrm{\Delta }p=\frac{nR}{V}\left(T_f-T_i\right)\\ \mathrm{\Delta }p=\frac{g}{s}\mathrm{\Delta }{m}_a\end{array}\}\Rightarrow \frac{g}{s}\mathrm{\Delta }{m}_a=\frac{nR}{V}\mathrm{\Delta }T\Rightarrow \boxed{{\displaystyle \mathrm{\Delta }{m}_a=\frac{s}{g}\frac{nR}{V}\mathrm{\Delta }T}}\end{array}$$

1. Betiko eran, barne-energiari berdin dio prozesu mota:

$$\mathrm{\Delta }U=c_{V}nR\mathrm{\Delta }T\Rightarrow \boxed{{\displaystyle \mathrm{\Delta }U=c_{V}nR(T_f-T_i)}}$$

2. Lana kalkulatzea oso erraza da, bolumena konstantea baita.

$$W=-\int pdV\Rightarrow W=-p\int dV\Rightarrow W=-p\mathrm{\Delta }V\Rightarrow W=0$$

bolumena konstantea baita.

3. Azkenik, beroari dagokionez, lanik egin ez duenez sistemak, barne-energiaren aldaketaren berdina da.

$$Q=\mathrm{\Delta }U\Rightarrow \boxed{{\displaystyle Q=c_{V}nR(T_f-T_i)}}$$

• Baina hori argi zegoen: bolumen konstanteko prozesua izanik, ezaguna ibilbidea, eta trukatutako beroa lortu daiteke $C_V$ bero-ahalmena zuzenean integratuz:

$$C_V\equiv \frac{\delta Q}{dT}\Rightarrow \delta Q=C_{V}dT\Rightarrow Q=C_V\mathrm{\Delta }T$$

Aurreko ariketan gertatu den modu berean ere, oraingo honetan bero-kantitatea lortzeko, prozesua gertatu den baldintzak kontuan hartuz, zuzenean kalkulatu daiteke: presioa konstante mantenduz edo bolumena konstante mantenduz, bero-ahalmenaren definizioa aplikatuz:

$$C={(\frac{\delta Q}{dT})}_{\text{baldintzak}}\Rightarrow \delta Q=C_{\text{baldintzak}}dT$$

$$\int \delta Q=\int C_{\text{baldintzak}}dT$$

---

Testuingurua

4. ARIKETA

Aurreko ariketako zilindroaren hormak adiabatikoak direla onartuko dugu, oraingo honetan, eta hasierako tenperatura, $T_i$.

• Zenbateko masa kantitate gehitu behar diogu pistoiari kuasiestatikoki, bukaerako tenperatura $T_f=k{T}_i$ izateko?

• Lortu $Q$, $W$ eta $\mathrm{\Delta }U$.

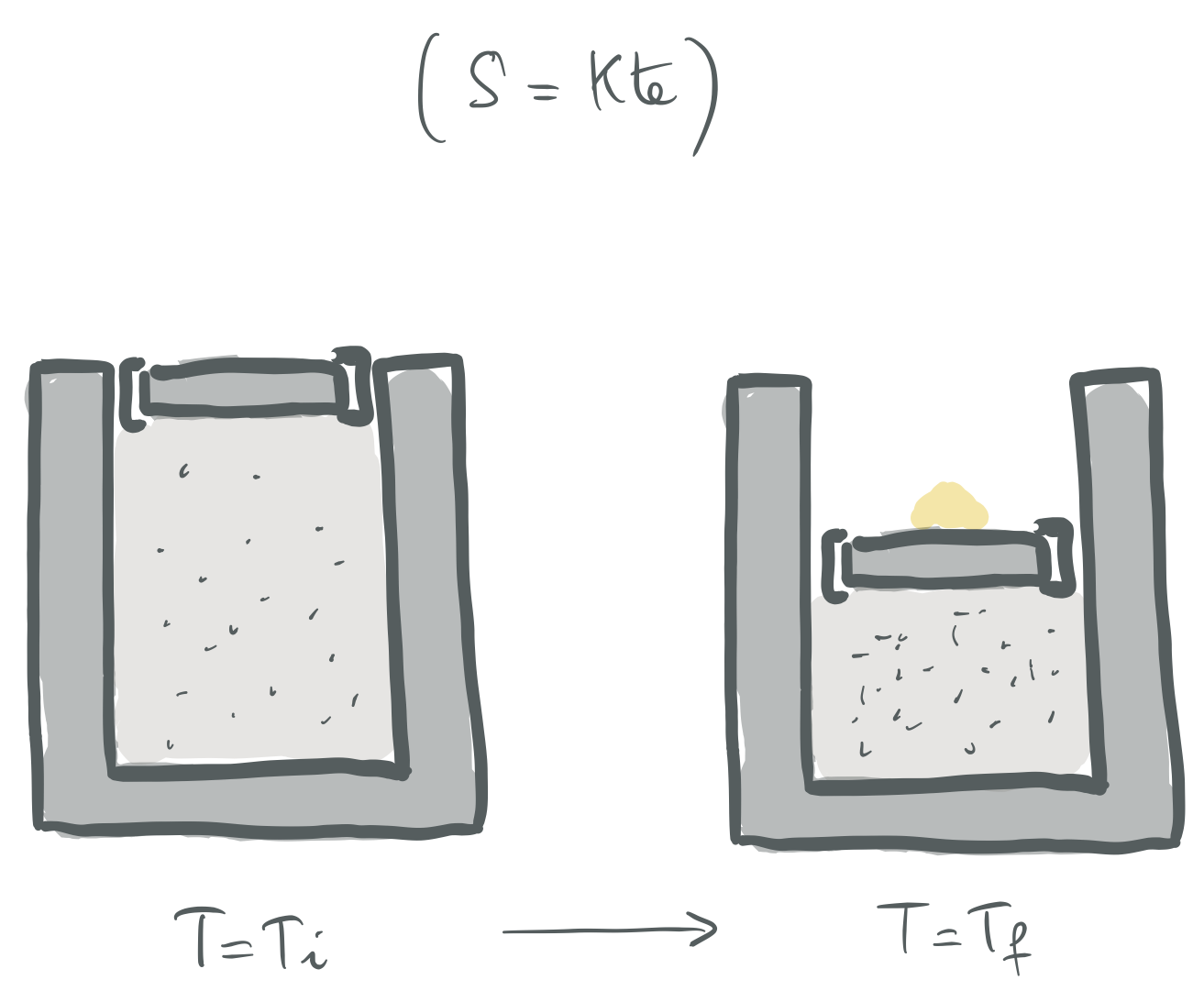
Prozesu adiabatikoa, ikusiko denez, isoentropikoa bera, fisikoki aurrera eramateko eratu daitekeenaren adierazpide grafikoa.

Emaitza

Ebazpen posible bat…

Prozesua adiabatikoa da; eta, beraz, sistemaren oreka-egoera ezaugarrituko dituzten aldagai guztien balioak aldatuko dira; ez edozein modutan, jakina, ondoko adierazpenetako bati segituz:

$$p{V}^{\gamma }=C$$

$$T{p}^{\frac{1-\gamma }{\gamma }}=C^{\prime }$$

$$T{V}^{\gamma -1}=C^{″}$$

Egoera-ekuazioa bera eta horietako bigarrena erabiliko dut, bukaerako oreka-egoerarekin lotutako aldagaien balioak kalkulatzeko:

• Hasierako egoera: ($T_i$, $p_i=\frac{Mg}{s}$, $V_i=\frac{nR{T}_i}{\frac{Mg}{s}}$)

• Bukaerako egoera: ($T_f=k{T}_i$, $p_f=\frac{(M+\mathrm{\Delta }m)g}{s}$, $V_f=\frac{nR{T}_f}{p_f}$)

$$\begin{array}{r}\begin{array}{l}{p}_f=p_i(\frac{T_i}{T_f}{)}^{\frac{\gamma }{1-\gamma }}\\ p_f=\frac{(M+\mathrm{\Delta }m)g}{s}\end{array}\}\Rightarrow \boxed{{\displaystyle \mathrm{\Delta }m=M[k^{\frac{1-\gamma }{\gamma }}-1]}}\end{array}$$

1. Prozesua adiabatikoa izan denez, honako hau bete da:

$$\boxed{{\displaystyle Q=0}}$$

2. Lehen Printzipioa aplikatuz, ondoko hau izango dugu: $\mathrm{\Delta }U=W$

$$\mathrm{\Delta }U=c_{V}nR(T_f-T_i)\Rightarrow \boxed{{\displaystyle \mathrm{\Delta }U=W=c_{V}nR\mathrm{\Delta }T}}$$

---

Iruzkinak

---

Aurreko horiek guztiak lortzeko badago beste modurik. Lehen printzipioaren adierazpen diferentziala izan daiteke abiapuntua. Jakina, horretarako, ondorioztatutako adierazpenetatik egokia aukeratu behar da; hots, aztergai den prozesuarekiko aldagai termodinamiko independente egokituak erabiltzen dituena.

Esaterako, prozesu isotermoaren kasuan, prozesua bera deskribatuta dago $T$ eta $p$ erabilita: hasierako eta bukaerako egoeren presioaren balioak aipatzen ditu enuntziatuak, batetik, eta, bestetik, prozesua isotermoa denez, tenperatura konstantea da, beraz, $dT$ nulua da. Orduan, prozesua aztertzeko aldagai termodinamiko egokituak dira zalantzarik gabe $p$ (balioak ezagunak dira) eta $T$ (berarekin lotutako atalak ez baitu ekarpenik egiten).

Honako hau da erabili beharreko lehen printzipioaren adierazpen diferentziala:

$$\delta Q=C_{p}dT+[-(C_p-C_V)\frac{{\kappa }_T}{\alpha }]dp$$

$$\begin{array}{r}\begin{array}{l}\delta Q=C_{p}dT+[-(C_p-C_V)\frac{{\kappa }_T}{\alpha }]dp\\ dT=0\Rightarrow C_{p}dT=0\end{array}\}\Rightarrow \boxed{{\displaystyle \delta Q=[-(C_p-C_V)\frac{{\kappa }_T}{\alpha }]dp}}\end{array}$$

Sistemari buruzko informazioa erabilita:

$$\begin{array}{r}\begin{array}{l}\delta Q=[-(C_p-C_V)\frac{{\kappa }_T}{\alpha }]dp\\ \\ \alpha =\frac{1}{T}\\ {\kappa }_T=\frac{1}{p}\\ (C_p-C_V)=-nR\end{array}\}\Rightarrow \boxed{{\displaystyle \delta Q=[-nR\frac{T}{p}]dp}}\end{array}$$

Baina $T=T_0$ eta aurreko ekuazio diferentziala zuzenean integratu daiteke:

$$\delta Q=[-nR\frac{T}{p}]dp\Rightarrow Q=-nR{T}_0\ln \left(\frac{p_f}{p_i}\right)$$

Puntu horretan, egoera-ekuazioa (mekanikoa) erabil daiteke berriro eta arestian lortutako emaitza berreskuratu:

Beste prozesuei dagokienez honako hauek dira lehen printzipioaren adierazpen egokiak, aldagai termodinamikoei dagokienez:

---

Isobaroa

$$\begin{array}{r}\begin{array}{l}\delta Q=C_{p}dT+[-(C_p-C_V)\frac{{\kappa }_T}{\alpha }]dp\\ dp=0\\ \\ \alpha =\frac{1}{T}\\ {\kappa }_T=\frac{1}{p}\\ (C_p-C_V)=-nR\end{array}\}\Rightarrow \boxed{{\displaystyle C_{p}dT}}\end{array}$$

Jakina, horixe da modua presio konstantea denean, horrek definitzen du ibilbidea diferentzial ez-zehatza kalkulatzeko, sistemak trukatu duen bero kalkulatzeko. Bestetik, kasu berezi $\mathrm{\Delta }U=C_V\mathrm{\Delta }T$ denez, gertatu den prozesua edozein izanda ere, hots, nahiz eta prozesuan presioa izan den konstante, barne-energiaren aldaketa ezaguna da. Gainera, lehen printzipioaren adierazpena (finitua, prozesu osoari dagokiona) aplikatuz, ondorioztatuko da lanari dagokion balioa. Dena dela, beti kalkulatu daiteke oso erraz, presio konstante izanik, honako hau baita: $W=-p_0\mathrm{\Delta }V$.

---

Isokoroa

$$\begin{array}{r}\begin{array}{l}\delta Q=C_{V}dT+\left[\frac{C_p-C_V}{V\alpha }\right]dV\\ dV=0\\ \\ \alpha =\frac{1}{T}\\ {\kappa }_T=\frac{1}{p}\\ (C_p-C_V)=-nR\end{array}\}\Rightarrow \boxed{{\displaystyle \delta Q=C_{V}dT}}\end{array}$$

Jakina, horixe da modua bolumena konstantea denean, horrek definitzen du ibilbidea diferentzial ez-zehatza kalkulatzeko, sistemak trukatu duen bero kalkulatzeko. Sistemak ez du lan mekanikorik egin, bolumena ez baitu aldatu. Beraz, barne-energiaren aldaketa da trukatu duen beroa. Dena dela, kasu berezi honetan argi zegoen, gas idealean $\mathrm{\Delta }U=C_V\mathrm{\Delta }T$ baita.

---

Adiabatikoa:

$$\begin{array}{r}\begin{array}{l}\delta Q=\left[\frac{C_p}{V\alpha }\right]dV+\left[\frac{{\kappa }_T}{\alpha }{C}_V\right]dp\\ \delta Q=0\\ \\ \alpha =\frac{1}{T}\\ {\kappa }_T=\frac{1}{p}\\ (C_p-C_V)=-nR\end{array}\}\Rightarrow \boxed{{\displaystyle 0=\left[\frac{C_p}{V\alpha }\right]dV+\left[\frac{{\kappa }_T}{\alpha }{C}_V\right]dp}}\end{array}$$

---

Prozesu berezi-berezia

Testuingurua

5. ARIKETA

Berogailu elektrikoaren bidez 500 m${}^3$-ko ikasgelaren tenperatura 10 graduan jaso dugu. Ikasgelaren presioak konstante dirau, zabalik dagoen leiho bati esker. Airea gas ideala dela onartuz, zenbatekoa izan da airearen barne-energiaren aldaketa?

Emaitza

Ebazpen posible bat…

Enuntziatuaren arabera gelako presioa eta bolumena ez dira aldatu; eta, hala ere, tenperatura aldatu da. Nola da posible hori? Printzipioz, egoera-ekuazioak presio, tenperatura eta bolumena lotzen ditu. Horietako bi finkaturik egonez gero, hirugarrena ere finkatuta dago. Baina, hori egia da, masa konstanteko sistemen kasuan. Aztertu beharreko sisteman, aldiz, masa ez da konstantea: leihoa zabalik dago. Deskribatutako prozesuan masa aldakorreko sistema dugu, ez masa konstantekoa, orain arte izan dugun moduan. Jakina, hori da arrazoia tenperatura aldatzeko.

Gelako gasa idealtzat hartu daitekeenez, ondokoa da barne-energiari dagokion adierazpena (egoera-ekuazio termikoa): $U=c_{V}nRT+K$. Barne-energiaren aldaketa lortzeko prozesuan parte hartu duten aldagaien aldaketak kontuan hartu behar ditugu. Gure kasuan $dn$ eta $dT$, esan bezala. Ondokoa da dugun barne-energiaren aldaketa diferentziala:

$$dU=d(c_{V}nRT)\Rightarrow dU=c_{V}d(nRT)$$

$nRT=pV$, konstantea dena; presioa eta bolumena aldatu ez baitira. Beraz $\boxed{{\displaystyle dU=0}}$. Barne-energiaren aldaketa nulua: masa-aldaketak tenperatura-aldaketa konpentsatuko du.

---

Gas idealak, aplikazioak

Testuingurua

6. ARIKETA

Zein da prozesu politropiko baten malda $p/V$ diagraman?

Emaitza

Ebazpen posible bat…

Ondokoa da prozesu politropikoaren definizioa: $p{V}^j=$ C. Horrelako prozesuari dagokion malda, $p/V$ diagraman, lortu behar denez, ondoko koefizientea kalkulatu behar da: $\frac{dp}{dV}$.

$p{V}^j=C$

$d(p{V}^j)=0$ $\Rightarrow$ $V^{j}dp+pj{V}^{j-1}=0$ $\Rightarrow$ $dp=-\frac{p}{V}dV$

$\boxed{{\displaystyle \frac{dp}{dV}=-j\frac{p}{V}}}$

$j$-ren balio konkretuek prozesu jakin batzuk definituko dituzte:

1. $j=\gamma$ prozesu adiabatikoa: ($S=$ kons.)

2. $j=1$ prozesu isotermoa: ($T=$ kons.)

3. $j=0$ prozesu isobaroa: ($p=$ kons.)

4. $j=\mathrm{\infty }$ prozesu isokoroa: ($V=$ kons.)

---

Testuingurua

7. ARIKETA

Airearen jokaera gas idealarena dela onartuz eta Hidrostatikaren Ekuaziotik abiatuz ($\text{d}p=-\rho g\text{d}h$), lortu presioak altuerarekiko duen mendekotasuna.

Emaitza

Ebazpen posible bat…

$dp=-\rho gdh$, non

1. $p$ presioa

2. $g$ grabitatea

3. $\rho$ airearen dentsitatea ($\rho =\frac{m}{V}$: $m$ airearen masa)

4. $h$ altuera; Lurraren gainazalarekiko neurtuta: erreferentzian $h=0$

Airea gas ideal moduan aztertu daitekeenez, enuntziatuaren arabera, gas idealaren egoera-ekuazio mekanikoa erabiliko da: $pV=nRT$, non $n=\frac{m}{M_m}$ mol-kopurua den. Informazio hori guztia esku artean dugula honako adierazpena lortu daiteke:

$p\frac{m}{\rho }=\frac{m}{M_m}RT\Rightarrow p=\frac{RT}{M_m}\rho$

Edo beste modua batean idatzita; eta abiapuntuko adierazpenean ordezkatuta:

$\rho =\frac{p{M}_m}{RT}\Rightarrow dp=-\frac{g{M}_m}{RT}pdh\Rightarrow \boxed{{\displaystyle \frac{dp}{p}=-\frac{g{M}_m}{RT}dh}}$

Azken ekuazio diferentzial hori integratu behar da. Horretarako, $T=T(h)$ funtzioa ezagutu beharko genuke. Demagun, dena den, integratu beharreko altuera-tartean (presio-tartean) tenperatura konstantetzat hartu daitekeela (lerro isotermoan integratzen ari gara, beraz). Horrela izanik, ekuazio diferentzialeko aldagaiak banatuta daude; eta integrazioa zuzena da:

$\boxed{{\displaystyle \ln \frac{p}{p_0}=-\frac{g{M}_m}{RT}\mathrm{\Delta }h}}\Rightarrow \boxed{{\displaystyle p=p_0{e}^{-\frac{g{M}_m}{RT}h}}}$

---

Testuingurua

8. ARIKETA

Fisikari mendizale batek honako altimetroa hau asmatu du: $\gamma$ konstante adiabatikoko gas idealez beteriko goma elastikoz egindako esferatxo adiabatikoa. Nola erabil dezake asmakizuna?

Emaitza

Ebazpen posible bat…

Aurreko ariketan lortu den emaitzaren arabera, zenbat eta Lurraren gainazalarekiko altuera handiagoa izan hainbat eta presioaren balio txikiagoak neurtuko dira; beti ere tenperatura aldatuko ez dela onartuko badugu. Altimetroa zer altueratan gauden jakiteko erabiliko dugu; kasu honetan, gauden altuera presioarekin lotuta dago Hidrostatikaren Ekuazioaren bidez. Mendian gora egiten den heinean, presioak (egurats-presioak) behera egiten duenez, esku artean dugun esferatxo adiabatikoaren bolumenak gora egiten du. Esferatxo adiabatikoa adiabatikoki isolatutako esferatxoa da; hots, prozesu adiabatikoa eragin diogu esferatxoan sartutako gas idealari. Gas idealaren prozesu adiabatikoari dagokion ekuazioa ondoko hau da:

$p{V}^{\gamma }=C\Rightarrow p_i{V_i}^{\gamma }=p_f{V_f}^{\gamma }$

Hortaz, presioa eta bolumena (esferatxoaren erradioa: $V=\frac{4}{3}\pi r^3$) lotuta daude: esferatxoaren erradioa neurtuz, presioaren balioa izango dugu. Eta azken hori ezagututa altuera kalkulatu dezakegu.

$p=p_i{e}^{-\frac{g{M}_m}{RT}h}\Rightarrow p=p_i{e}^{-ch}$

$p_i(\frac{4}{3}\pi {r_i}^3{)}^{\gamma }=p_f(\frac{4}{3}\pi {r_f}^3{)}^{\gamma }\Rightarrow p_i{{r_i}^3}^{\gamma }=p_i{e}^{-ch}{{r_f}^3}^{\gamma }$

${{r_i}^3}^{\gamma }=e^{-ch}{{r_f}^3}^{\gamma }\Rightarrow e^{ch}={\left({\displaystyle \frac{r_f}{r_i}}\right)}^{3\gamma }$

$ch=3\gamma \ln \left({\displaystyle \frac{r_f}{r_i}}\right)\Rightarrow \boxed{{\displaystyle h=\frac{3}{c}\gamma \ln \left({\displaystyle \frac{r_f}{r_i}}\right)}}$

Hidrostatikaren Ekuazioa erabili dugu. Beraz, inplizituki onartu dugu tenperatura ez dela aldatu; mendian gora egin dugun altuera-tartean, behintzat. Aldatu ez dena egurats-tenperatura da; esferatxoan sartu dugun gas idealaren tenperatura, aldiz, aldatu da, prozesu adiabatikoa eragin baitiogu. Hortaz, asmakizunaren aldaera proposatu daiteke: esferatxoaren bolumena (erradioa) erabili beharrean, esferatxoan sartutako termometroa erabil daiteke. Gas idealaren prozesu adiabatikoan, tenperatura presioarekin ondoko ekuazioaren bidez lotuta dago: $p{T}^{\frac{1-\gamma }{\gamma }}=C$.

Beste alde batetik, eta berriro ere gas idealaren egoera-ekuazio mekanikoa erabiliz, ondokoa adierazpena lortu daiteke:

${\left({\displaystyle \frac{r_f}{r_i}}\right)}^3\propto {\left({\displaystyle \frac{V_f}{V_i}}\right)}^3\Rightarrow {\displaystyle \frac{{\left({\displaystyle \frac{nRT}{p_f}}\right)}^3}{{\left({\displaystyle \frac{nRT}{p_i}}\right)}^3}}$

${\displaystyle \frac{V_f}{V_i}}={\displaystyle \frac{T{p}_i}{T_{i}p}}$

${\displaystyle \frac{p_i}{p}}={\left({\displaystyle \frac{T}{T_i}}\right)}^{{\displaystyle \frac{1-\gamma }{\gamma }}}$

Eta, beraz, aurreko adierazpenean dena ordezkatuz, honako hau lortuko da:

$h={\displaystyle \frac{\gamma }{c}}\ln {\left(\frac{T}{T_i}\right)}^{\frac{1}{\gamma }}\Rightarrow \boxed{{\displaystyle h=\frac{1}{c}\ln \frac{T}{T_i}}}$

---

Testuingurua

9. ARIKETA

Har itzazu aintzakotzat zilindro baten barnean dauden gas ideal baten $N$ molak. Gas idealaren $C_V$ eta $C_p$ bero-ahalmenak konstanteak dira. Hasierako egoeran, gasaren bolumena eta tenperatura $V_i$ eta $T_i$ dira, hurrenez hurren. Gasa kuasi-estatikoki zabaldu da amaierako bolumena eta presioa $V_f=k{V}_i$ eta $p_f$ izan arte. Bukaerako presioa 1 atm da. Lortu:

• Indize politropikoa,

• $\mathrm{\Delta }U$, $Q$ eta $W$.

Emaitza

Ebazpen posible bat…

1. Indize politropikoa lortzeko, prozesu politropikoari dagokion adierazpena eta gas idealaren egoera-ekuazio mekanikoa erabiliko dira:

   $$\begin{array}{r}\begin{array}{l}p{V}^j=C\Rightarrow p_i{V}_i^j=p_f{V}_f^j\\ pV=nRT\Rightarrow p=\frac{nRT}{V}\end{array}\}\Rightarrow \frac{nR{T}_i}{V_i}{V}_i^j={\left(k{V}_i\right)}^j\Rightarrow nR{T}_i{V}^{j-1}=k^j{V}^j\Rightarrow k^j=\frac{nR{T}_i}{V_i}\end{array}$$
   $$j\ln k=\ln \frac{\ln R{T}_i}{V_i}\Rightarrow \boxed{{\displaystyle j=\frac{\frac{nR{T}_i}{V_i}}{\ln k}}}$$

2. $\mathrm{\Delta }U$

   Gas ideala denez, badakigu ondoko adierazpena beteko dela: $\mathrm{\Delta }U=c_{V}nR\mathrm{\Delta }T$. Berdin dio zer motatako prozesua gertatu den; gas idealaren kasuan, horrela definitu dugulako, barne-energiak tenperaturarekiko baino ez dauka mendekotasuna; eta ekuazio hura beti erabil daiteke: prozesu adiabatikoetan, isotermoetan, isobaroetan, isokoroetan

   $\mathrm{\Delta }U=c_{V}nR(T_f-T_i)\Rightarrow \boxed{{\displaystyle \mathrm{\Delta }U=c_{V}nR(\frac{k{V}_i}{nR}-T_i)}}$

3. Lana kalkulatzeko, lanaren definizioa bera erabiliko dugu:

   $\delta W=-pdV\Rightarrow \int \delta W=\int -pdV\Rightarrow W=\int p(V)dV$

   $$\begin{array}{r}\begin{array}{l}p{V}^j=C\Rightarrow p=\frac{C}{V^j}\\ {W=-\int \frac{C}{V^j}dV\Rightarrow W=-C\int \frac{dV}{V^j}\Rightarrow W=-p_i{V}_i^j\frac{1}{-j+1}{V}^{-j+1}]}_{V_i}^{V_f}\\ W=p_i{V}_i^j\frac{1}{1-j}(V_f^{-j+1}-V_i^{-j+1})\\ W=\frac{1}{1-j}(p_f{V}_f^j{V}_f^{-j+1}-p_i{V}_i^j{V}_i^{-j+1})\Rightarrow W=\frac{1}{1-j}(p_f{V}_f-p_i{V}_i)\Rightarrow W=\frac{nR}{1-j}(T_f-T_i)\end{array}\end{array}$$

4. Azkenik, beroa kalkulatzeko lehenengo Printzipioa erabiliko da:

   $Q=\mathrm{\Delta }U-W$

   $\boxed{{\displaystyle Q=(T_f-T_i)[c_V-\frac{nR}{-j+1}]}}$

---

Testuingurua

10. ARIKETA

• Jarraitu al diezaioke gas ideal monoatomikoak irudian adierazi den prozesuari?

• Eta gas ideal diatomikoak?

  Baiezkoan, zein gasetan gertatuko da tenperatura-aldaketarik handiena?

• Zer gertatzen da $U$ barne-energiarekin?

Onartu bi gas idealen mol kopuruak berdinak direla.

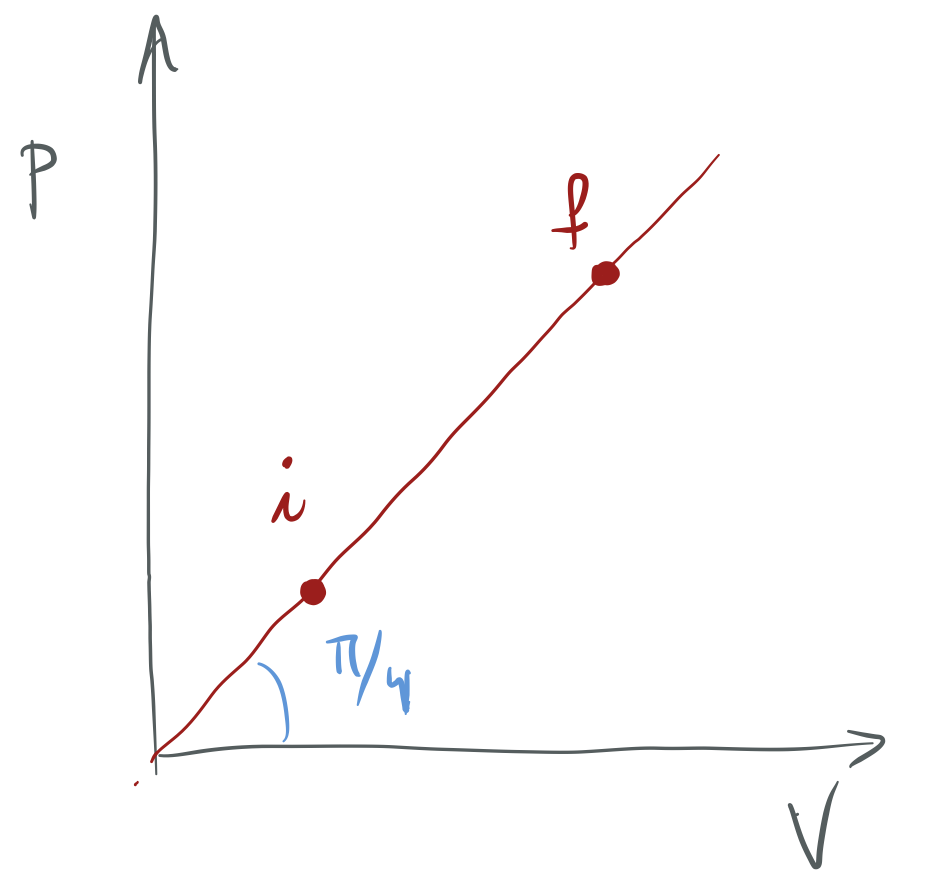
Proposatutako prozesua, $p/V$ diagraman, $i$-tik $f$-rakoa.

Emaitza

Ebazpen posible bat…

Biek bete dezakete ibilbidea; ez dago izaeraren arabera. Gas idealari bi egoera-ekuazio dagokio: mekanikoa, $pV=nRT$; eta termikoa, $U=c_{V}nRT+k$. Egoera-ekuazio mekanikoak ez du nabarituko gas ideala monoatomikoa ala diatomikoa den: hartan ez baita ageri partikula osatzaileen ezaugarririk (ez dago izaeraren berririk, beraz). Aldiz, egoera-ekuazio termikoak bai nabarituko du: horretan, izaeraren marka baitago, $c_V$ hain zuzen ere. Hortaz, bien bukaerako tenperatura berdina izango da: $T_f=\frac{p_f{V}_f}{nR}$.

Bien bukaerako $(p,V)$ oreka-egoera berbera denez, lanari dagokionez ez dago alderik bien artean: biek egingo dute lan berbera. Jakina, irudian agertu den ibilbideak definitutako $p/V$ diagramako lerrotik beherako eta limiteen arteko azaleraren balioa da lana.

Gas bien arteko aldeak $\mathrm{\Delta }U$ barne-energian agertuko dira, esan bezala. Orduan, eta Lehenengo Printzipioaren arabera, prozesuaren ondorioz lan-kantitate berbera egingo dute; eta, beraz, bata bestea baino errentagarriago izango da. Hots, batak besteak baino bero gutxiago behar izango du lan bebera egin ahal izateko.

$$\begin{array}{r}\begin{array}{c}{C}_{V\text{ mono }}<C_{Vdi}\\ {(\mathrm{\Delta }U=nR{C}_V)}_{\text{mono }}<{(\mathrm{\Delta }U=nR{C}_V)}_{\text{di }}\\ (\mathrm{\Delta }U-W{)}_{\text{mono }}<(\mathrm{\Delta }U-W{)}_{\text{di }}\Rightarrow Q_{\text{mono }}<Q_{\text{di }}\end{array}\end{array}$$

---

Testuingurua

11. ARIKETA

Monoatomikoa eta diatomikoa diren bi gas (ideal) desberdinak tenperaturaren eta bolumenaren balio berberen bidez ezaugarritu ditugu.

Haien bolumenak hasierako balioaren erdira izan arte konprimitu ditugu adiabatikoki.

1. Zein dago tenperatura handiagoan?

Emaitza

Ebazpen posible bat…

Prozesua adiabatikoa da; eta, beraz, sistemaren oreka-egoera ezaugarrituko dituzten aldagai guztien balioak aldatuko dira; ez edozein modutan, jakina, ondoko adierazpenetako bati segituz:

1. $p{V}^{\gamma }=C$

2. $T{p}^{\frac{1-\gamma }{\gamma }}=C^{{}^{\prime }}$

3. $T{V}^{\gamma -1}=C^{{}^{″}}$

Kasu honetan erabili beharreko aldagaiak $V$ eta $T$ dira; eta, beraz, prozesu adiabatikoa deskribatzen duten ekuazioetako azkena erabiliko dugu $T_f$ bukaerako tenperatura kalkulatzeko.

$$\begin{array}{r}\begin{array}{l}{T}_f=T_i(\frac{V_i}{V_f}{)}^{\gamma -1}\\ V_i=2V_f\end{array}\}\Rightarrow \boxed{{\displaystyle T_f=T_i{2}^{\gamma -1}}}\end{array}$$

Adierazpen hori edozein gas ideali dagokio: monoatomikoa zein diatomikoa izan. Aipatu bi horien arteko aldea $\gamma$ balioan dago: ${\gamma }_{\text{mono}}=\frac{5}{3}$ eta ${\gamma }_{\text{di}}=\frac{7}{5}$. Beraz, ondokoa da gas bien bukaerako tenperaturen arteko zatidura:

$$\begin{array}{r}\begin{array}{l}{T}_{f\text{mono}}=T_{i\text{mono}}{2}^{\gamma -1}\\ T_{f\text{di}}=T_{i\text{di}}{2}^{\gamma -1}\end{array}\}\Rightarrow \frac{T_{f\text{mono}}}{T_{f\text{di}}}=\frac{T_{i\text{mono}}}{T_{f\text{di}}}\frac{2^{{\gamma }_{\text{mono}}-1}}{2^{{\gamma }_{\text{di}}-1}}\Rightarrow \boxed{{\displaystyle \frac{T_{f\text{mono}}}{T_{f\text{di}}}=2^{\frac{4}{15}}\approx 1.2}}\end{array}$$

---

Zikloak

Ondoren datozen ariketetan, sistema, edo sistemak, gas ideala(k) izango d(ir)a, aurrekoetan bezalaxe. Oraingo hauetan, aldiz, ariketen helburua zikloak aztertzea eta horietan trebatzea da.

Arestian aipatu den moduan, gas idealak direnez, gas idealarekin lotutako taula beti erabil daiteke, kontrakorik esan ezean.

datuak
e-e mekanikoa	$pV=nRT$
e-e termikoa	$\mathrm{\Delta }U=C_{V}nRT$
bero-ahalmenak	$c_V$	$c_p$	Mayer-en erlazioa
monoatomikoa	$\frac{2}{3}$	$\frac{5}{3}$	$nR$
diatomikoa	$\frac{5}{3}$	$\frac{7}{3}$	$nR$
indize adibatikoa: $\gamma =\frac{c_p}{c_V}$	monoatomiko: $\frac{5}{3}$	diatomiko: $\frac{7}{5}$
koefiziente esperimentalak	$\alpha =\frac{1}{T}$	${\kappa }_T=\frac{1}{p}$

Oso gomendagarria da, kasu hauetan ere bai, irudiak, eskemak, grafikoak egitea. Gehienetan, ikusiko duzunez, $p/V$ diagrametan adierazi beharreko zikloak deskribatzen dira. Irudikatu eta horietan adierazi zer datu ezagutzen duzun, direla egoerak, direla prozesu motak eta horiekin lotutako adierazpenak (ekuazioak, egokia diren diagrametan…). Berebat adierazi zer eskatzen dizun enuntziatuak. Horrela eginez gero, berehala konturatuko zara erabili beharreko prozeduraz. Askotan termo irakasgaian gertatzen den moduan, modu asko erabil daiteke, ibilbide asko dago, abiapuntu batetik helmuga-puntura heltzeko. Denbora galtzeko ez bazaude, ondo apuntatu zer eskatzen zaizun eta zer datu duzun.

Testuingurua

12. ARIKETA

Esku artean ditugun gas idealaren 4 mol termikoki isolatuta dagoen zilindroan daude, 6 atm-n eta ${27}^{\circ }$ C-ko tenperaturan. Bat-batean, zilindroa itxi duen pistoia askatu da. Ondorioz, gasa 1 atm-eko kanpo-presioaren kontra zabaldu da. Gasak bete duen bolumena hirukoiztu da.

Lortu ondokoak:

1. amaierako tenperatura,

2. barne-energiaren aldaketa,

3. trukatutako beroa, eta egindako lana.

$(C_V=\frac{3}{2}R)$

Emaitza

Ebazpen posible bat…

---

Testuingurua

13. ARIKETA

Gas ideal bati, 300 K-eko tenperaturan dagoena eta 1 mol-ekoa bera, bolumena bikoiztu dion beroketa isobarikoa eragin diogu. Ondoren, hozketa isokoroaren bidez presioaren balioa hasierako presioaren erdira jaitsi dugu. Azkenik, hasierako egoerara eraman duen konpresio isotermoa eragin dugu. Prozesu guztiak itzulgarriak dira.

Lortu $Q$, $W$, $\mathrm{\Delta }U$ (eta $\mathrm{\Delta }S$) azpiprozesu guztietarako, eta ziklo osorako.

Emaitza

Ebazpen posible bat…

---

Testuingurua

14. ARIKETA

Esku artean duzun nitrogeno kantitatearen egoerari dagozkion ezaugarriak honako hauek dira: $p_1=8$ atm, $V_1=3$ l, $T_1={25}^{\circ }$ C.
Beste egoera batean aldiz, sistema ezaugarrituko duten aldagai termodinamikoen balioak, hauexek dira: $V_2=4,5$ l eta $p_2=6$ atm.

Lortu:

1. Gasak jasotako bero kantitatea, egoera batetik bestera joandakoan.

2. Zabaldutakoan, gasak egindako lana.

3. Gasaren barne-energiaren aldaketa.

Emaitza

Ebazpen posible bat…

---

Testuingurua

15. ARIKETA

Ebatz ezazu ariketa berbera, honako kasu hauetan:

• Hasierako egoeratik amaierako egoerarako ibilbidea ABD denean.

• Hasierako egoeratik amaierako egoerarako ibilbidea ACD denean.

Ibilbideak alboko irudian adierazi dira.

Emaitza

Ebazpen posible bat…

---

Testuingurua

16. ARIKETA

Gas ideal baten 1 mol, $p_0$ eta $V_0$ balioetako egoeran dago eta honako ziklo honi segitzera behartu dugu:

• 2$p_0$ presiorainoko prozesu isotermoa.

• 2$V_0$ bolumenerainoko prozesu isobarikoa.

• $p_0$ presiorainoko prozesu isokoroa.

• Hasierako egoerara eramango duen prozesu isobaroa.

1. Irudikatu zikloa, $p/V$ diagraman.

2. Lortu zikloarekin etekina eta alderatu aipatu zikloko muga-tenperaturen artean arituko litzatekeen Carnoten zikloari dagokionarekin.

$(C_V=\frac{3}{2}R)$.

Emaitza

Ebazpen posible bat…

---

Testuingurua

17. ARIKETA

Makina termiko batek aldameneko irudiko zikloa bete du. $C_V$ eta $C_p$ bero-ahalmenak konstanteak direla onartuz, zenbatekoa da makinaren etekina?

Makinaren $\mu$ etekina 1 izan liteke?

Hartu kontuan $m$ eta $n\ge 1$ direla. Arbitrarioak izan daitezke?

Emaitza

Ebazpen posible bat…

---

Testuingurua

18. ARIKETA

Gas ideal baten 1 mol $(C_V=\frac{5}{2}R)0^{\circ }$ C-tik ${50}^{\circ }$ C-ra isokoroki berotu da. Ondoren, ${100}^{\circ }$ C-ra, isobarikoki berotu. Espantsioaren ondorioz tenperatura ${75}^{\circ }$ C-ra beheratu da. Azkenik, hasierako egoeraraino isobarikoki, hoztu. Ziklo osoan zehar sistemak 74,5 Kcal xurgatu ditu.

1. Lortu $Q$, $W$ eta $\mathrm{\Delta }U$ zikloaren prozesu guztietarako.

2. Zein motatako prozesua da hirugarrena?

Emaitza

Ebazpen posible bat…

---

Testuingurua

19. ARIKETA

Gas ideala ondoko zikloa betetzera behartu dugu:

• konpresio isokoro itzulgarria, ($p_1$, $V_1$) $\to$ ($p_2$, $V_1$).

• espantsio adiabatiko itzulgarria, ($p_2$, $V_1$) $\to$ ($p_1$, $V_2$).

• konpresio isobaro itzulgarria, ($p_1$, $V_2$) $\to$ ($p_1$, $V_1$).

1. Irudika ezazu zikloa $p/V$ diagraman.

2. Demagun 1 mol dugula, eta $V_2=6$ l dela.
   Lortu gasak emandako eta xurgatutako bero kantitateak, eta zikloaren etekina.
   Eman ezazu emaitza $p_1$, $V_1$ eta $R$ parametroen funtzioan.

Emaitza

Ebazpen posible bat…

---

Testuingurua

20. ARIKETA

Gas ideal baten 1 mol-ek bi lerro isotermoz eta bi lerro isokoroz osatutako zikloa bete du. Gasaren bolumena $V_1=3{\text{m}}^3$-tik $V_2=6{\text{m}}^3$-ra aldatu da, eta gasaren presioa $p_1=1$ atm-tik $p_2=2$ atm-ra aldatu da.

Aldera itzazu sistemak kanporatu duen lana eta zikloan ageri diren muga-tenperaturen artean arituko litzatekeen Carnot-en zikloari dagokiona.

Espantsio isotermoan sistemaren bolumena bikoiztu da.

Emaitza

Ebazpen posible bat…

---