Apunteak

06 Gaia: Termodinamikaren bigarren printzipioa

---

Historias del metabolismo. ¿Por qué somos simios caros?

Juan Ignacio Pérez Iglesias explica cómo el metabolismo humano requiere mucha energía para mantener en funcionamiento el cerebro y otros procesos biológicos.

Publicado: 17/10/2022 15:58 (UTC+2) Última actualización: 17/10/2022 15:58 (UTC+2)

---

1. Somos simios caros.

2. La vida del metabolismo.

---

6. Gaia:, 6Z, 7Z, 8Z

Iruzkinak:

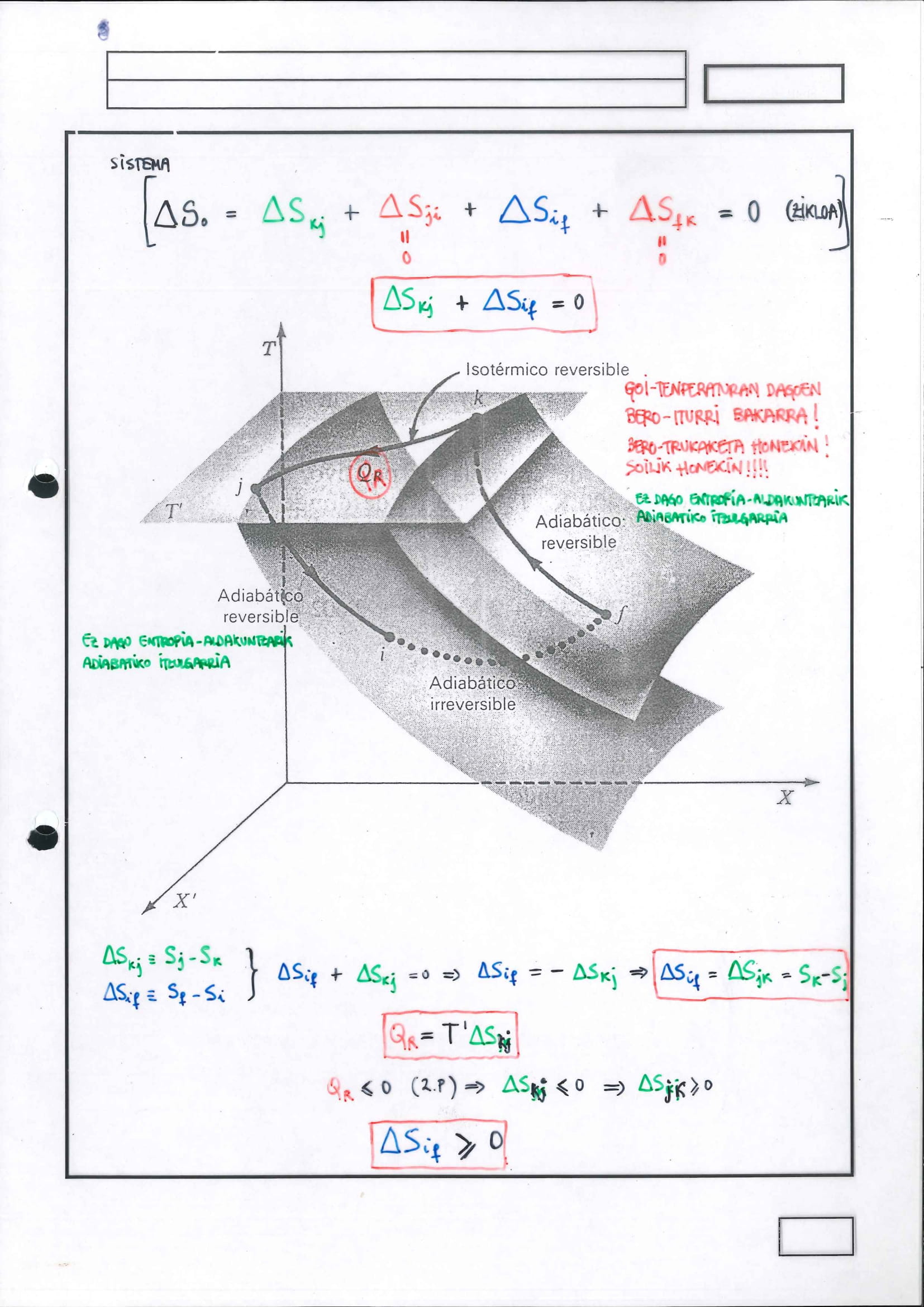
1. Bigarren Printzipioak esaten du posibleak diren prozesuen artean, hots, Lehen Printzipioarekin bat egiten dutenen artean, zein gertatzen diren berez Lehen Printzipioaren arabera edozein prozesu gerta daiteke aurrera zein atzekoz aurrera, noranzko batean energia kontserbatzen bada, kontrakoan, baita ere Horixe da beheko irudian adierazi dena

   

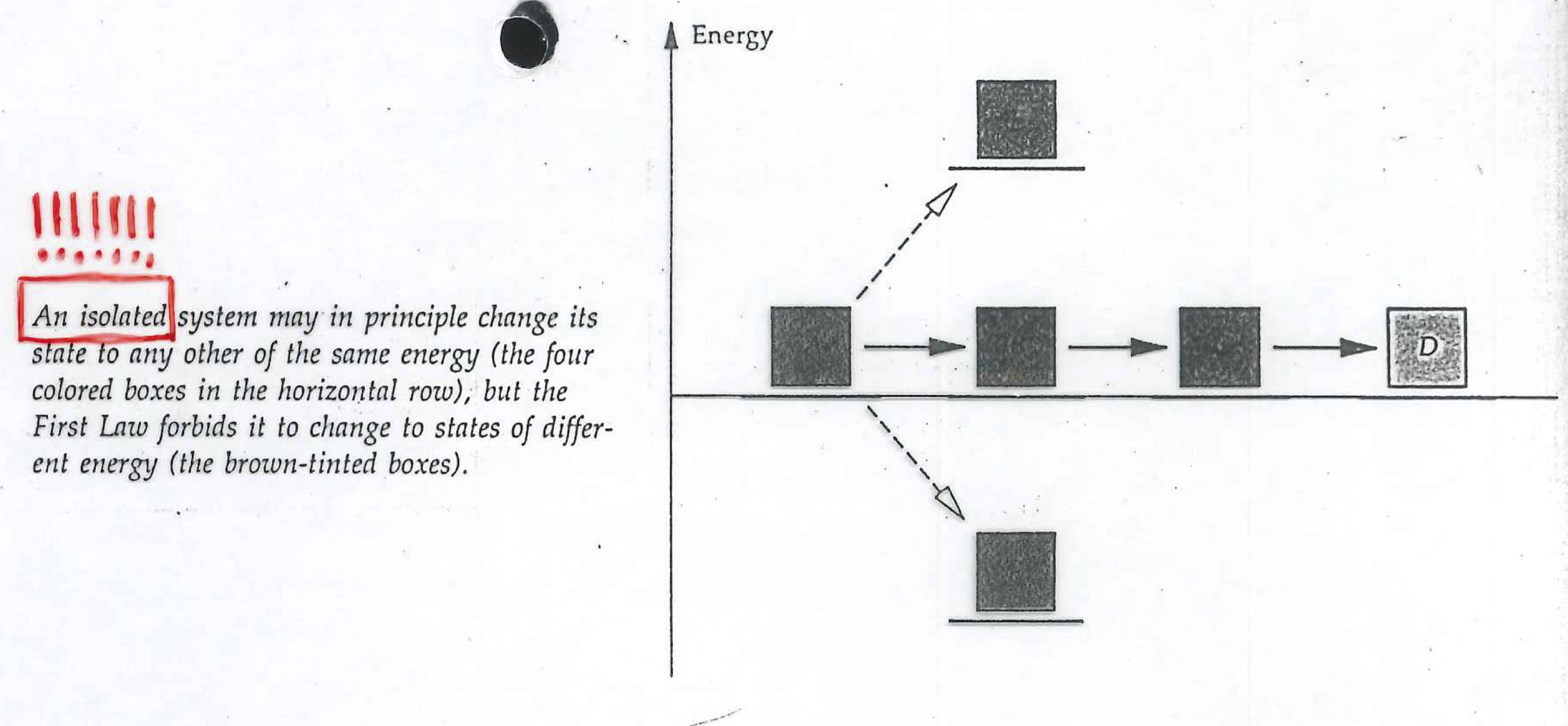
   Lehen eta bigarren Printzipioen eduki fisikoa.

   • ordenatuetan dago unibertsoari (erabat isolatutako sistemari, beraz,) dagokion energia eta, abzisetan egoerak daude, egoera orokorrak, edozein egoera.

   • Lehen Printzipioaren arabera, energia kontserbatzen da (ez da ezer egin behar horretarako, Izadia arduratzen da horretaz) eta, beraz, ordenatu bereko egoerak baino ezin ditu lotu edozein prozesuk.

   • Hala ere, posiblea da $i$-tik $f$-rako eta $f$-tik $i$-rako prozesuak, kontrako noranzkokoak haiek, ordenatu berean baitaude eta, ondorioz, energia berekoak dira: unibertsoaren energia berekoak

   • posiblea da ordenatu berean ez dauden egoerak lotzen dituzten prozesuak eragitea, baina kasu horietan, eskua sartu beharko da; eskua sartuta, unibertsoa aldatzen da: eskua sartzean ingurunearekin lotzen baita, edozein modutan (edozein askatasun-graduren bidez) ordura arte benetako unibertsoa zena

   • Bigarren Printzipioak argitzen du ordenatu berean dauden egoeren arteko zer prozesu gertatzen den berez: $i$-tik $f$-rakoa edo $f$-tik $i$-rakoa

2. Esan bezala, berez gertatzen den prozesua ez dago debekatuta, baina zerga dauka berarekin lotuta: aurrera eraman ahal izateko, eskua sartu egin behar da eta hori, Izadian, energia gastatzea da. Ez dago dena galduta baina!

   • berezko prozesua erabil daiteke berezkoa ez den prozesua eragiteko, horretarako, aipatutako bi prozesuak akoplatu behar dira. Jakina, prozesu efektiboak bat egin behar du Bigarren Printzipioarekin, oraingo honetan, Entropia-emendioaren forman emanik, esaterako.

   • Entropia-emendioaren arabera, guztiz isolatutako (unibertsoaren) entropia-aldaketaren zeinua finkatuta dago:

   $$\boxed{{\displaystyle \mathrm{\Delta }{S}_{i\to f}^U\ge 0}};\mathrm{\Delta }{S}_{i\to f}^U\equiv \mathrm{\Delta }{S}_{i\to f}^{ing}+\mathrm{\Delta }{S}_{i\to f}^{sis}=0$$

   • Baina $\mathrm{\Delta }{S}_{i\to f}^U$ definizioaren arabera, edozein konbinazio da posible, baturaren zeinua errespetatuz: horrexegatik pentsatu dezakegu, pentsatzea ez baita berezko prozesua

6.1 Izadiko asimetria

• Ez da ezer frogatuko, aldiz, argumentuak erabiliko dira onargarritasuna onartzeko; hots, dena da ideal

• Izadian asimetria dago: prozesu batzuk berez (naturalki, era naturalean, …) gertatzen dira noranzko batean, baina ez kontrakoan baina ez dira gertatzen era naturalean, berez, kontrako noranzkoan…

• asimetria horren adierazgarri:

  • lana $\leftrightarrow$ beroa transformazioak, Z liburuan aztertzen dira Kontuan izan zer eredu erabiltzen den transformazio mota hori aztertzeko: sistemaren egoera ez da aldatzen. Oso garrantzitsua da ereduaren ezaugarriak ondo ezagutzea, bestela, ez dabil.

  • denon esperientzia dira honako hauek:

    • inork ez du inoiz ikusi beroa tenperaturaren maldan gora

    • inork ez du inoiz ikusi mahai batean, esaterako, pausagunean dagoen pilotak berez, besterik gabe, gora egiten

  • horiek guztiak, eta gehiago, dira asimetriaren aurpegiak

6.2 Zikloak eta makina termikoak

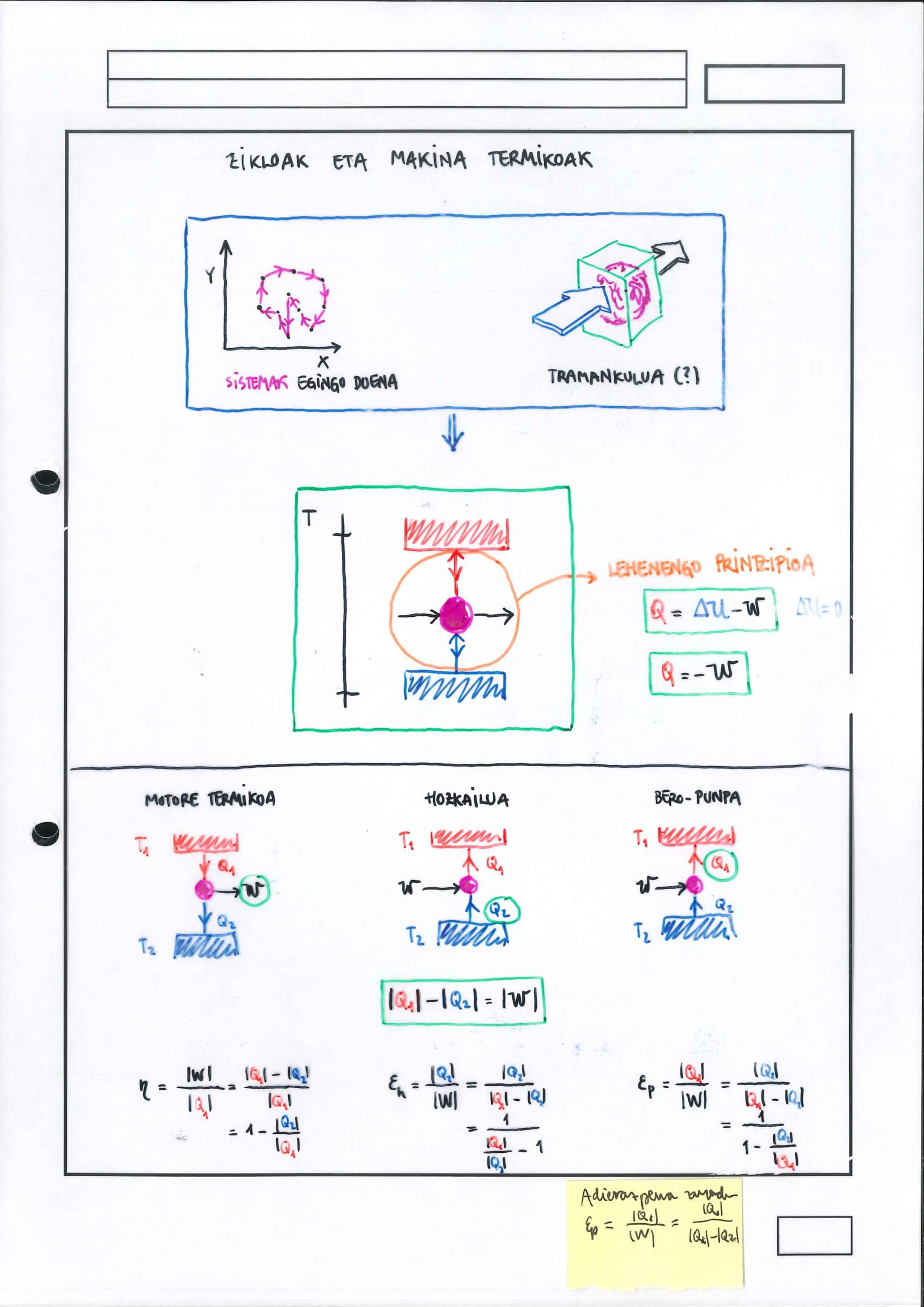
• eskua sartuz, berezkoak ez diren prozesuak abiarazteko zikloak eta makinak (termikoak) beharrezkoak dira

• makina termikoetan beti erabiltzen da eskema grafiko berbera horretan, bi bero-iturri baino ez dira adierazten, baina, kontuz!, horrek ez du esan nahi bi bero-iturrik baino ez duela beti parte hartzen edozein ziklotan:

  • goi-tenperaturan dagoen bero-iturri bakarrak adierazten du efektiboa izan den (ziklikoki dabilen) sistemaren bero-xurgapena, nahiz eta xurgapen-azpiprozesu asko (bat baino gehiago) egon daitezkeen zikloan

  • behe-tenperaturan dagoen bero-iturri bakarrak adierazten du efektiboa izan den (ziklikoki dabilen) sistemaren bero-kanporatzea, nahiz eta kanporatze-azpiprozesu asko (bat baino gehiago) egon daitezkeen zikloan

  • jakina, sistema bera da erreferentzia (erreferentzia-sistema) bero-trukeei dagokienez

• lehen printzipioa aplikatzen zaio ziklikoki dabilen sistemari:

$${[Q=\mathrm{\Delta }U-W]}_{\text{ziklikoki dabilen sistema}}$$

• ziklikoki dabilenez: $\mathrm{\Delta }U=0$ eta, orduan, $Q=-W$

• hiru makina termiko aztertuko da eta beti erabiliko da eskema grafiko berbera, nahiz eta interpretazio bana duten makinek, helburu banakoak baitira makinak:

  • motor termikoa:

    • helburua da tenperatura-diferentzia aprobetxatzea lana egiteko

    • berarekin lotutako parametroa $\eta$ errendimendua (etekina) da, neurtzen du zenbat lan ateratzen den sartutako energia unitateko: $\eta =\frac{|W|}{|Q_{\downarrow |}}$

  • hozkailua:

    • helburua da tenperatura-diferentzia sorraraztea, horretarako, lana egin behar da

    • berarekin lotutako parametroa $ϵ$ efizientzia (etekina) da, neurtzen du zenbat energia (bero moduan) ateratzen den hoztu nahi den sistematik, sartutako lan unitateko: $ϵ=\frac{|Q_{\uparrow }|}{|W|}$

  • bero-ponpa:

    • helburua da goi-tenperaturan dagoen sistema bati energia (bero moduan) ematea, horretarako lan egin behar da

    • berarekin lotutako parametroa ${ϵ}_p$ efizientzia (etekina) da, neurtzen du zenbat energia (bero moduan) sartzen den goi tenperaturan dagoen sisteman, horretarako erabil den energia (lan) unitateko: ${ϵ}_p=\frac{|Q_{\uparrow }|}{|W|}$

• makina horiek guztiak ezaugarritzeko erabiltzen diren errendimenduak positiboak dira horrexegatik beti erabili behar dira balio absolutuak

• errendimenduen adierazpenetan agertzen diren $|W|$ lanak beti dira:

  $$|W|=|Q_{\uparrow }|-|Q_{\downarrow }|$$

  edo

  $$Q_{\uparrow }+Q_{\uparrow }(\equiv Q)=-W$$

6.3 Termodinamikaren Bigarren Printzipioaren (bi) enuntziatu

• 2.garren Printzipioaren zenbait enuntziatu dago; oraingo honetan klasikoenak aztertuko dira.

• Ematen du ez dutela inolako loturarik, baina asimetria berberaren bi aurpegi baino ez dira.

• Kontuz! Izugarri garrantzitsua da inolako eraginik gabe, eskua sartu gabe, besterik gabe… modukoak beti esatea enuntziatuak aipatzen direnean. Horrelakorik aipatu ezean, ez zaio Izadiko asimetriari erreferentzia egiten:

  • posiblea da hotz dagoen sistematik beroago dagoen beste sistema batera energia pasatzea (pasaraztea), prozesuaren noranzko hori ez dago debekatuta, baina, horretarako eskua sartu egin behar da: lana egin behar da.

  • posiblea da oso-osorik beroa lan bihurtzea, baina bero hori da bi bero efektiboren arteko batura aljebraikoa; hots, badago eraginik, bero eran pasatzen zaio energia inguruneari eta, bide batez, lana egiten da

• Atkins-i segituz: 2. Printzipioarekin lotutako aldagai termodinamikoa $S$ entropia da, askatasun-gradu termikoarekin lotutako aldagai estentsiboa bera, $T$ tenperaturaren aldagai konjokatua

6.4 Termodinamikaren Bigarren Printzipioaren bi enuntziatuen baliokidetasuna

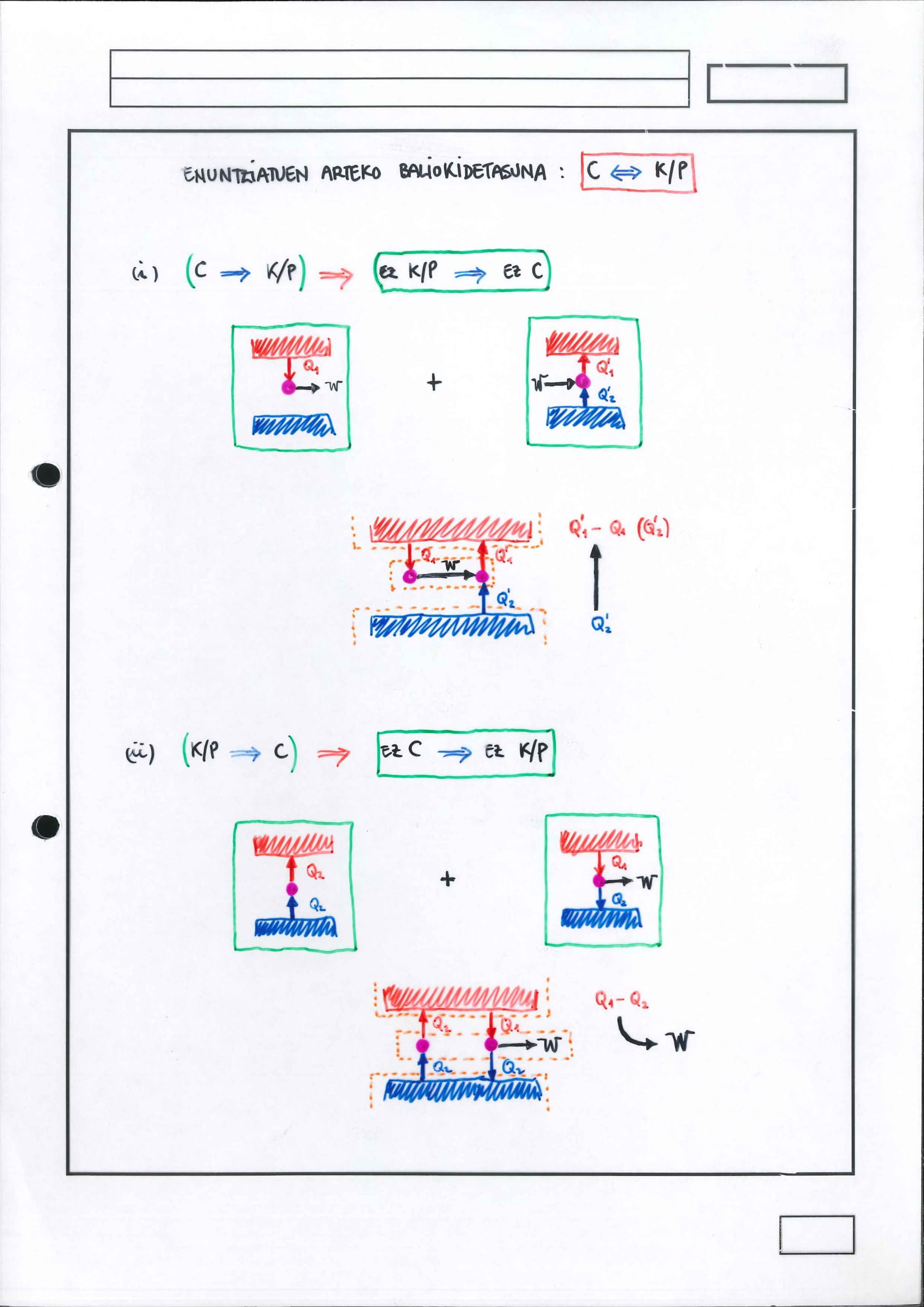
6.5 Itzulgarritasuna/itzulezintasuna kontzeptua

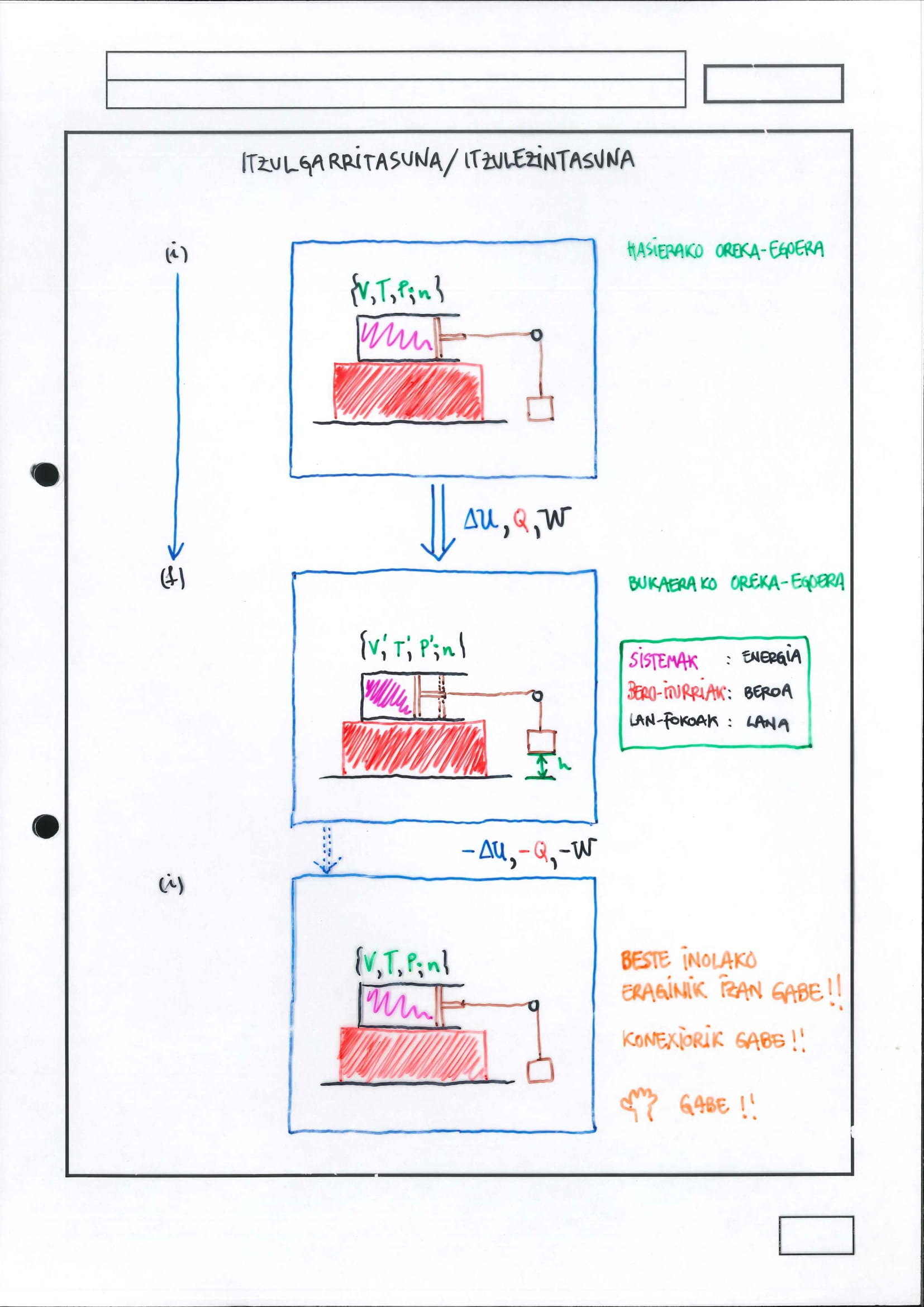
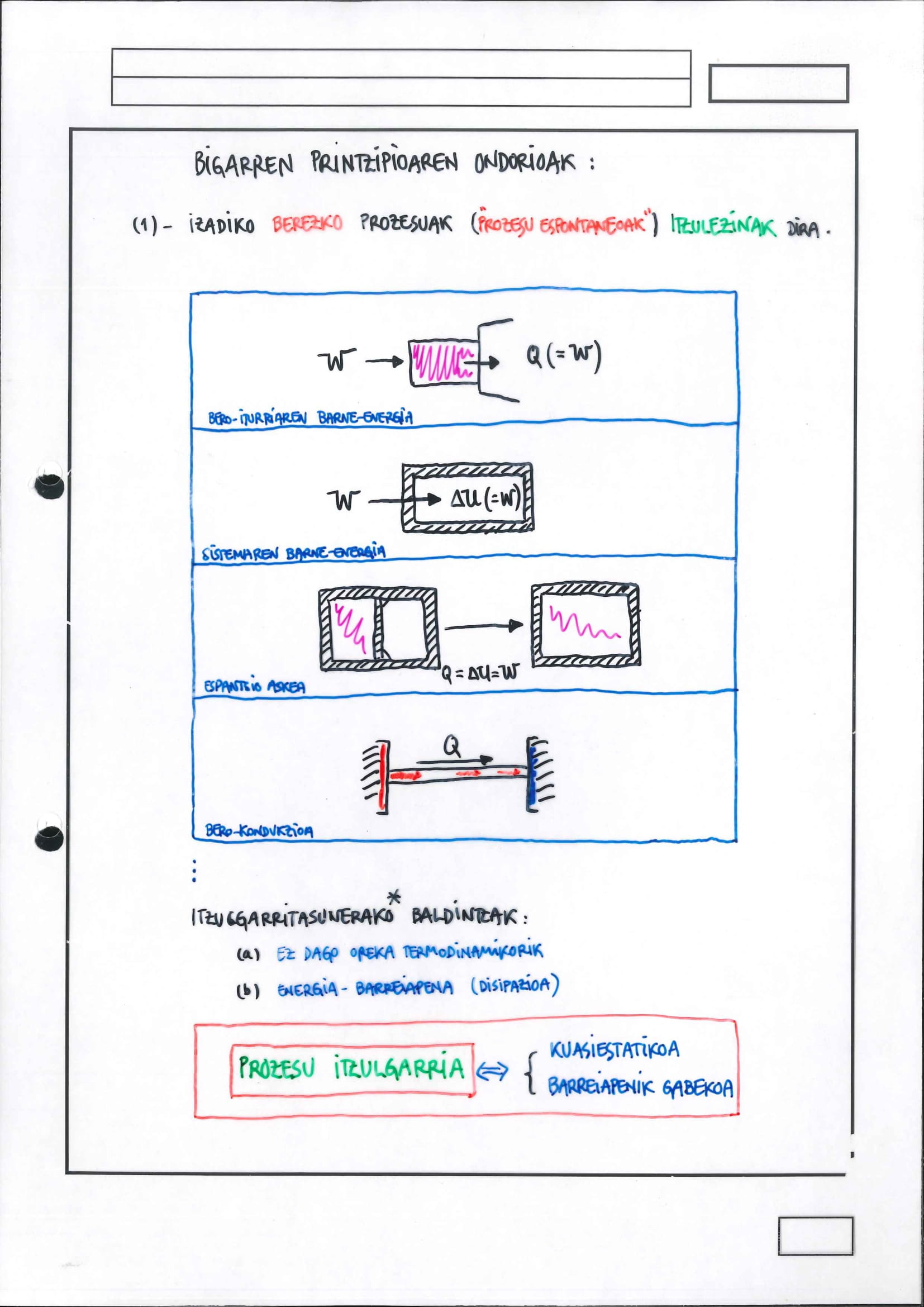
6.6 Bigarren Printzipioaren Ondorioak:

1. 6.6.1 Izadiko berezko prozesuak itzulezinak dira

   

• Berezko prozesuen sailkapenak eta aztertzeak hiru ondorio dauka:

  1. berez gertatzen diren prozesuei buelta emateko, kontrako noranzkoan eragiteko, Bigarren Printzipioaren aurka egin behar da; beraz, ezinezkoak dira kontrako noranzkokoak eta, ondorioz, berez gertatzen diren prozesuak itzulezinak dira

  2. hortaz, horrexegatik, propietate komuna dute berezko prozesuek: energia-barreiatzea, edozein motatakoa, haiekin lotuta dago: barreiatutako energia hori, bero moduan, da lan bihurtu beharko litzakeena buelta emateko prozesuari…ezinezkoa bera

  3. aipatutako propietate komun horren bidez, ondorioztatzen dira itzulgarritasunerako baldintzak: prozesuak izan behar du, aldi berean,

     • kuasiestatiko

     • energia-barreiaketarik gabeko

• metodo axiomatikoa:

  • Caratheodory-ren enuntziatua:

    

    ikus honako hau

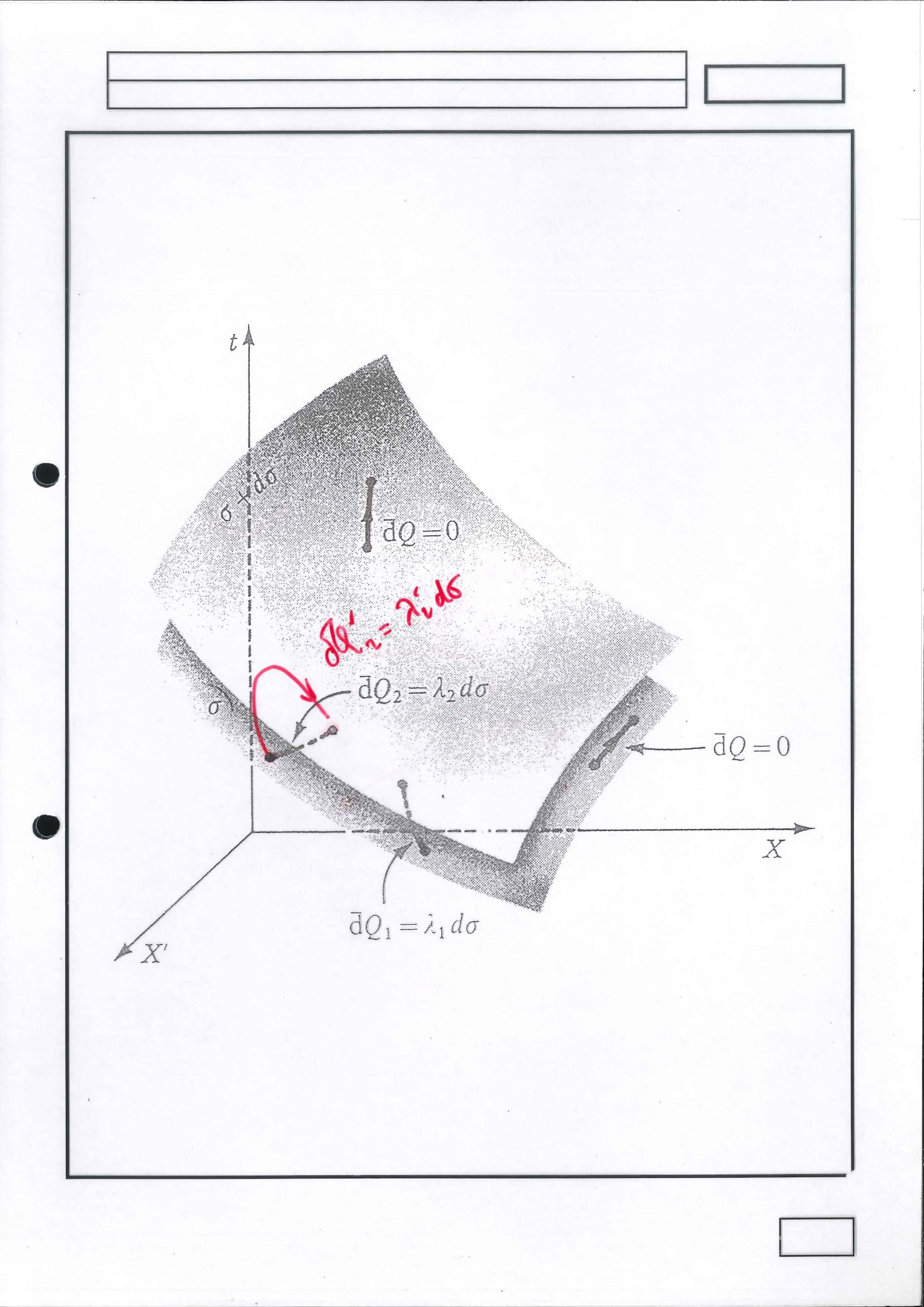
  2. Gainazal Adiabatikoen Existentzia:

     • aldagai bakarreko sistema

       • kasu honetan lehen printzipioa baino ez da behar, ez da bigarren printzipioaren potentzia osoa behar

       • dena dela, kontuan hartu behar da behin baino gehiagotan aipatutakoa: aztertzen den prozesua ez da soilik kuasiestatiko; aldi berean itzulgarria da

       • esan bezala, hori ez da azpimarratzen liburuan, nahiz eta bai komentatzen den

       • gogoratu gas idealaren kasuan lortu direla prozesu adiabatiko kuasiestatikoei dagokien forma (edozein diagramatan): prozedura berbera da

     • aldagai anitzeko sistema

       

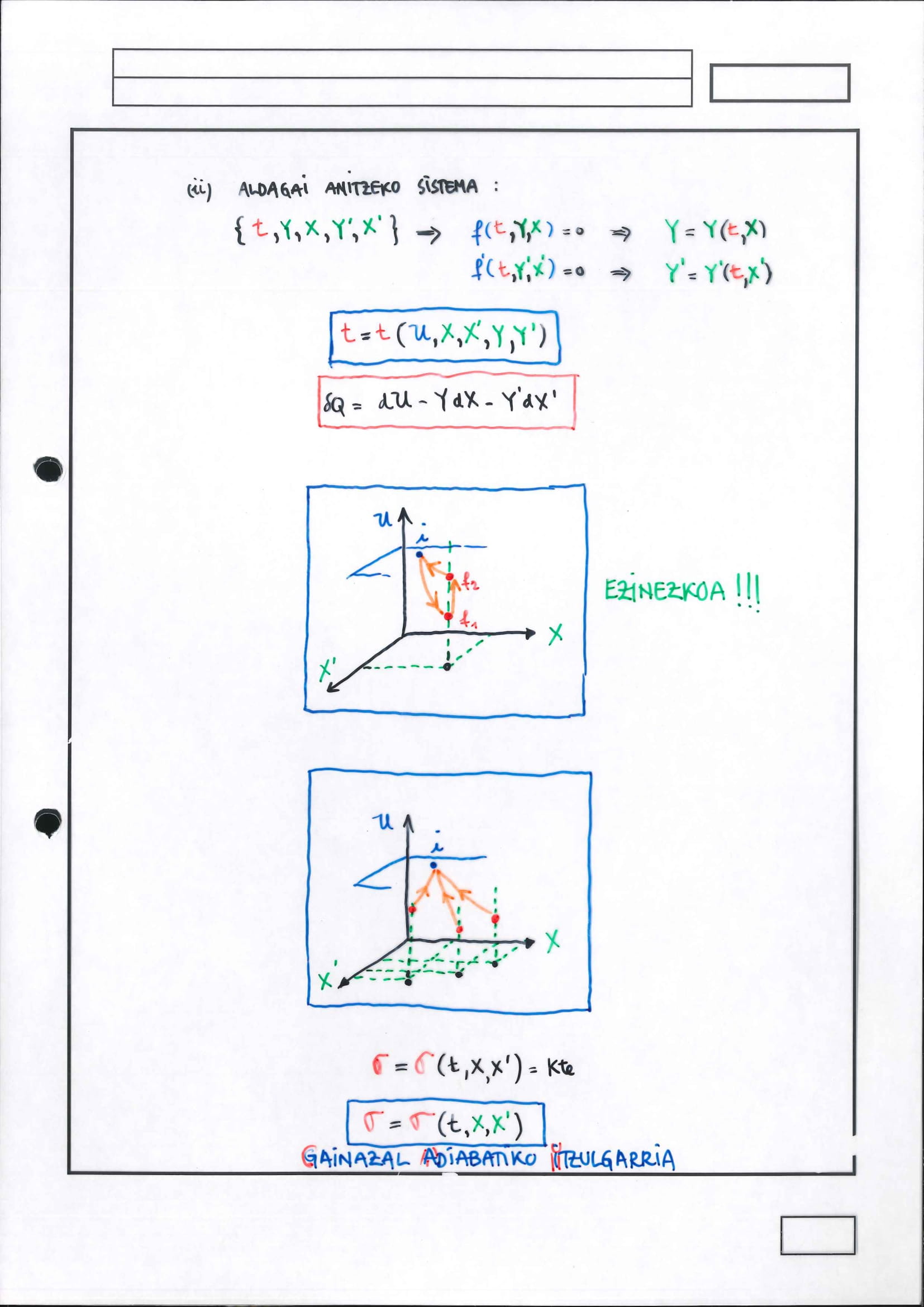
       • Aldagai anitzeko edozein sistemaren kasuan derrigorrean erabili behar da 2. printzipioaren indar osoa

       • frogapena egin da konfigurazio-espazio berezi batean: hiru dimentsiokoa (fisikoki sistemak hiru askatasun-gradu baino ez dauka) baino ez bera, nahiz eta ondorioa erabat orokorra den eta, gainera, askatasun-graduak deskribatzeko erabili diren aldagaiak dira $U,X,X^{\prime }$: sistemaren barne-energia eta bi desplazamendu orokortu. Denak dira estentsiboak

       • nahikoa da diagrama bakarrean lortzea frogapena

       • ondorio da: $\sigma =\sigma (U,X,X^{\prime })$ funtzioa existitzen dela (edozein sistemaren kasuan)

       • existitzen den funtzioa denez:

         • $\sigma$ gainazal adiabatiko itzulgarriz bete daiteke konfigurazio-espazioa

         • diferentzial zehatza da

         • sistemaren propietate bat adierazteko erabil daiteke, beste edozein aldagai termodinamikoren antzera

         • aldagai independenteen sortakoa izan daiteke eta, beraz, esaterako, honako hau idatz daiteke: $U=U(\sigma ,X,X^{\prime })$; konfigurazio-espazioko aldagaitzat hartuta

       • Gainazal adiabatiko itzulgarriek ezin dute elkar ebaki: hala balitz, frogapenean erabilitako argumentu berberak erabiliz berriro 2. Printzipioaren aurka egingo luke ziklo hipotetikoak eta kontraesana ondorioztatu beharko litzateke

  3. $\delta Q$-ren faktore integratzailea

     

     • Edozein sistemaren kasuan eta edozein prozesu itzulgarritan, kuasiestatiko eta energia-barreiaketarik gabeko bera, sistemak trukatzen duen beroa beti da honako hau:

     $${\boxed{{\displaystyle \delta Q={\left(\frac{\partial U}{\partial \sigma }\right)}_{X,X^{\prime }}\cdot d\sigma }}}_{(1)}\Rightarrow \delta Q=\lambda \cdot d\sigma \Rightarrow {\boxed{{\displaystyle \frac{\delta Q}{\lambda }=d\sigma }}}_{(2)}$$

     • beroak ez du galtzen bere ez-zehatz izaera: beroa beti da diferentzial ez -zehatza, baina, era itzulgarrian trukatutako beroak beti dauka faktore integratzailea

     • frogapenetik ondorioztatzen da, derrigorrean honako hauek identikoki nuluak direla:

     $${\left(\frac{\partial U}{\partial X}\right)}_{\sigma ,X^{\prime }}-Y=0$$
     $${\left(\frac{\partial U}{\partial X^{\prime }}\right)}_{\sigma ,X}-Y^{\prime }=0$$

     • hots, beti betetzen dira: definiziotzat har daitezke, horien moduko orokor bat baino ez da idatziko, errazteko:

     $$\boxed{{\displaystyle Y\equiv {\left(\frac{\partial U}{\partial X}\right)}_{\sigma ,X^{\prime },\dots }}}$$

     • barne-energia aldagai estentsiboen, independenteak izanik, funtzioan idatzitakoan, edozein deribatu partzialek definitzen du bere aldagai intentsibo konjokatua

       grafikoki

       

     • oso interesantea da adierazpide grafikoan agertzen diren prozesuak aztertzea eta deskribatzea (ariketa-proposamena)

  • Faktore integratzailearen esangura fisikoa

    

    • honako hau $\delta Q=\lambda (t,X,X^{\prime },\cdots )\cdot d\sigma$, beste ere honetan idatz daiteke:

    $$\boxed{{\displaystyle \delta Q=\varphi (t)\cdot f(\sigma )d\sigma }}$$

    • egiatan, faktore integratzailea $\varphi (t)$ baino ez da, $\frac{\delta Q}{\varphi (t)}$ diferentzial zehatza baita

    • faktore integratzailean ez da (edozein) sistemari buruzko informazioa agertzen

    • faktore integratzailean soilik agertzen da $t$ tenperatura (balioa)

    • $t$ hori ez da sistemaren tenperatura-funtzioa, baizik eta sistema dagoen, beroa trukatzen duen heinean, egoera termikoari esleitu zaion tenperaturan balioa

    • faktore integratzailea unibertsala da: sistemak era itzulgarrian bero-trukea egin duen egoera termikoaren menpekoa baino ez da; beroa trukatzen den egoera termikoen menpekoa

    frogapena

    

    • oso interesantea da frogapena, trebatzeko (ariketa-proposamena)

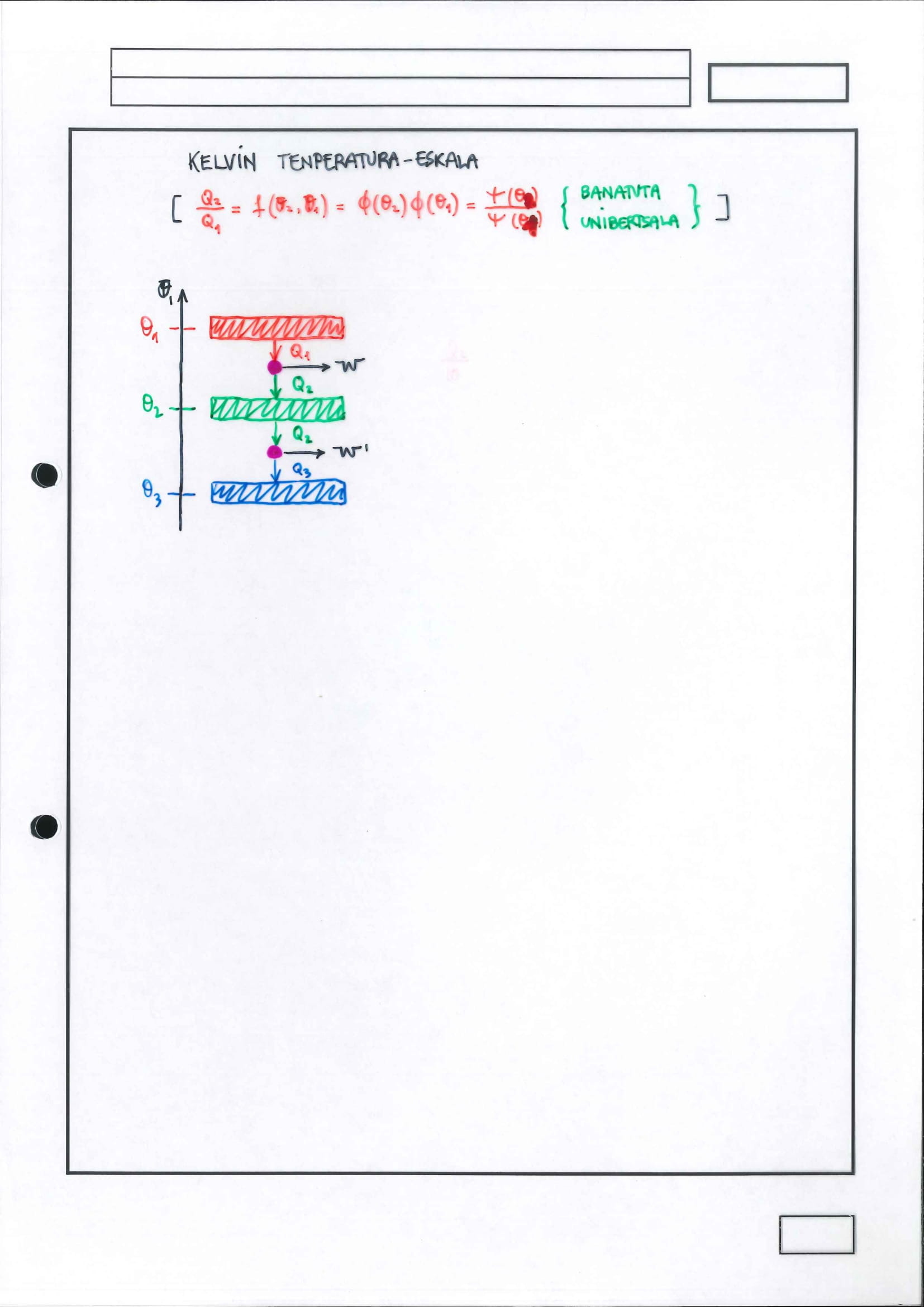
  4. Kelvin tenperatura-eskala*

     

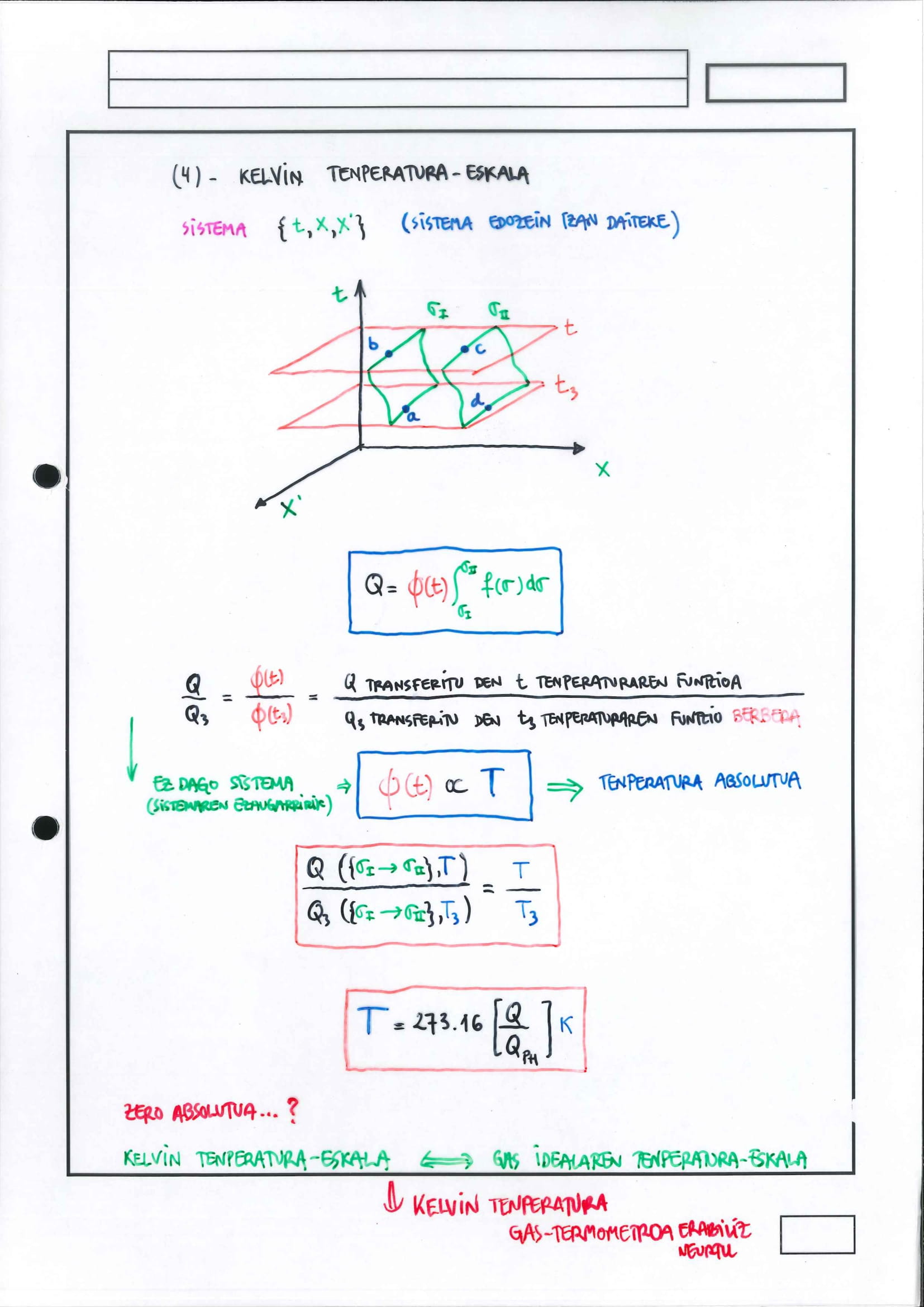
     • unibertsaltasun horrek ahalbidetzen du tenperatura-eskala absolutua definitzea

     • Tenperatura-eskala absolutuaren definizioan erabiltzen den aldagai termometrikoa da sistema batek $t$ tenperaturaren balioaz ezaugarritutako egoera termikoan dagoela, tenperatura konstantean, eta era itzulgarrian trukatzen duen beroa

     • tenperatura horretan trukatutako beroak badauka mendekotasuna:

       • sistemarekiko

       • ibilbidearekiko

     • baina erreferentziarako hartutako egoera termikoan trukatutako beroaz zatituz gero, beroen arteko zatidurak ez dauka ez sistemarekiko ezta ibilbiderekiko mendekotasunik ere, egoera termikoarekikoa baino ez, erreferentziarako hartutako egoera termikoa bada tenperatura-eskalaren definizioan kontuan hartu beharreko puntu finkoetako bat

• 6.6 Bigarren Printzipioaren Ondorioak

  • Ondorioak 5. Entropia-funtzioaren existentzia

    

    • $\delta Q=\lambda (t,X,X^{\prime })\cdot d\sigma$

    • $\lambda (t,X,X^{\prime })=\varphi (t)\cdot f(\sigma )$

    • $\varphi (t)\propto T\Rightarrow \boxed{{\displaystyle \varphi (t)=k\cdot T}}$

    $$\delta Q=[k\cdot T]\cdot [f(\sigma )\cdot d\sigma ]\Rightarrow \delta Q=T\cdot [kf(\sigma )d\sigma ]$$
    $$\boxed{{\displaystyle \stackrel{\text{IG}}{\overbrace{\frac{\delta Q}{T}}}=\underset{\text{sistema}}{\underbrace{kf(\sigma )d\sigma }}}}$$

    • edozein sistemak era itzulgarrian (eta egoera termiko jakinean, $T$ tenperaturan, beraz; aldatzekotan, itzulgarriki aldatzen da) trukatzen duen beroaren faktore integratzailea da (bero-trukea gertatu den) $T$ tenperatura absolutua

    • diferentzial zehatza da sistemaren atala sistemari dagokion propietatea adieraziko du $S$ ikurrez adierazten da eta entropia deritzo

    $$\boxed{{\displaystyle dS\equiv \frac{\delta Q^{IG}}{T}}}$$

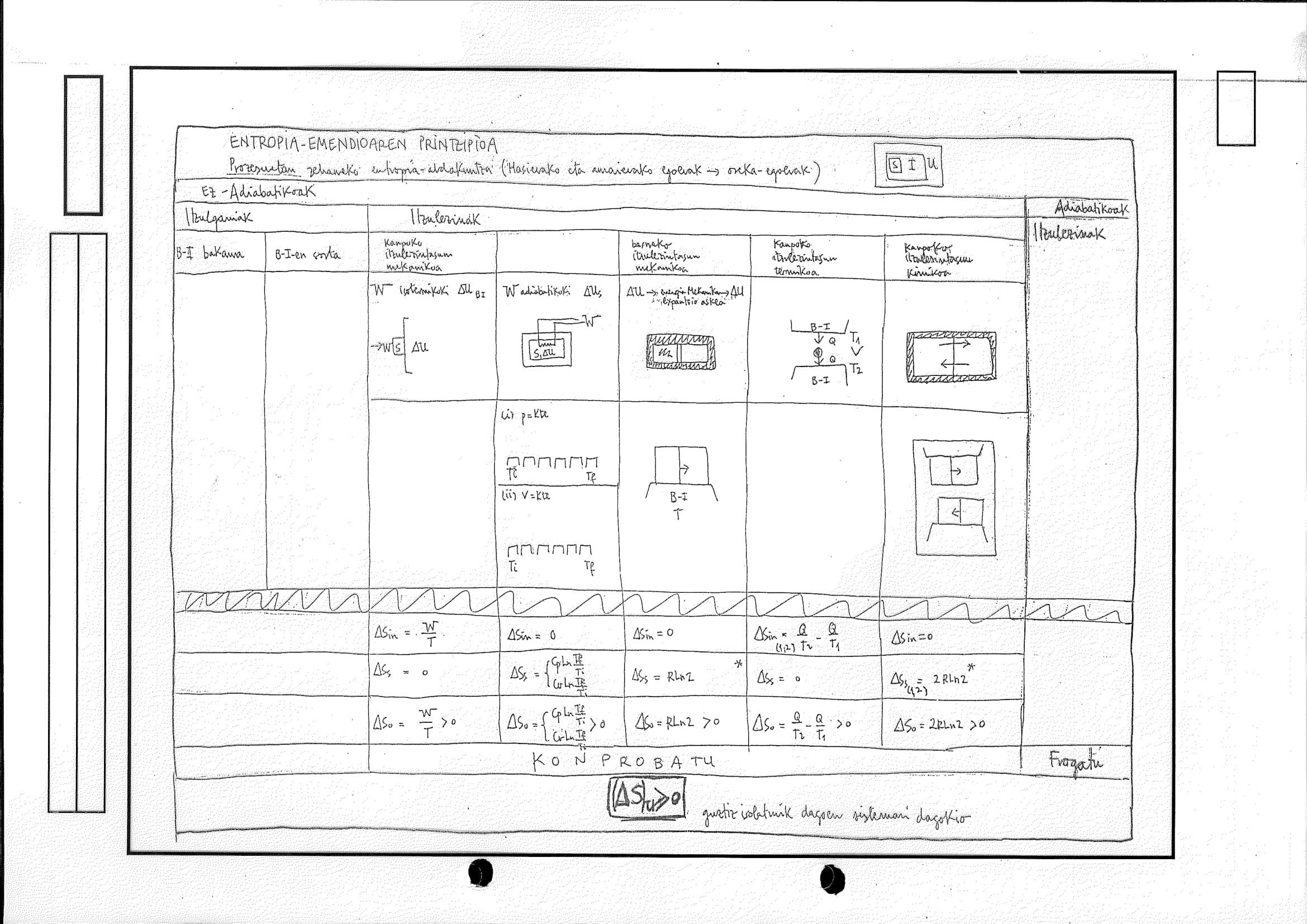
  • Laburbilduma

    

    • Edozein sistemaren kasuan

    • Edozein prozesuren kasuan

      • itzulezin (IE)

      • itzulgarri (IG)

    • Beti kalkulatu daiteke prozesu horretan sisteman gertatu den entropia-aldaketa

    • Horretarako, 2 tresna:

      

      1. Bigarren Printzipioa, entropia-funtzioaren eragiketa-definizioa: $dS=\frac{\delta Q^{IG}}{T}$

      2. Lehenengo Printzipioa, era itzulgarrian trukatutako beroaren adierazpen diferentziala: $\delta Q^{IG}={[dU-\delta W]}^{IG}$

      3. Biak aldi berean:

      $$\boxed{{\displaystyle dS=\frac{{[dU-\delta W]}^{IG}}{T}}}$$

    • Prozesua IG bada, zuzenean aplikatu goikoa

    • Prozesua IE bada, IE-ak lotu dituen $i$ eta $f$ berberak lotuko dituen edozein prozesu IG aukeratu eta goikoa aplikatu

      • egokia den ordezko prozesu IG, horrek esan nahi du: ondo aukeratzea prozesua deskribatzeko erabiliko diren aldagai independenteak

      • gehienetan aldagairen bat konstantea izango da: sartu hori aldagai independenteen sortan, bere aldaketak ez baitu ekarpenik egingo eta entropiaren kalkulua erraztuko da

---

• Adibidea

  

  • gas idealaren

    

    kasuan (sistema jakina zeinaren informazio guztia, ia-ia, ezaguna den) edozein prozesutan kalkulatu daiteke zer entropia-aldaketa gertatu zaion

  • Iruzkina:

    • Bi askatasun-graduko (edo orokorrean, bi askatasun-gradu martxan baino ez duen) sistemaren kasuan, entropia deskribatzeko honako bi aldagai independenteen sortak aukeratu daitezke, besteak beste:

      • $(T,V)$:

        • Beraz, $S=S(T,V)\Rightarrow dS={\left(\frac{\partial S}{\partial T}\right)}_{V}dT+{\left(\frac{\partial S}{\partial V}\right)}_{T}dV$,

        • $V$ konstanteko baldintzatan, $[dS{]}_V={\left[{\left(\frac{\partial S}{\partial T}\right)}_{V}dT\right]}_V$

        • $V$ konstanteko baldintzatan sistemak trukatu duen beroa da: $\delta Q=C_{V}dT$

        • Eta entropiaren eragiketa-definizioa kontuan hartuz: $dS=\frac{\delta Q}{T}\Rightarrow dS=\frac{C_{V}dT}{T}\Rightarrow {[dS=\frac{C_{V}dT}{T}]}_V$

        • Hauxe da ondorioa:

        $$\boxed{{\displaystyle {\left(\frac{\partial S}{\partial T}\right)}_V=\frac{C_V}{T}}}$$

      • $(T,p)$:

        • Beraz, $S=S(T,p)\Rightarrow dS={\left(\frac{\partial S}{\partial T}\right)}_{p}dT+{\left(\frac{\partial S}{\partial p}\right)}_{T}dp$,

        • $p$ konstanteko baldintzatan, $[dS{]}_p={\left[{\left(\frac{\partial S}{\partial T}\right)}_{p}dT\right]}_p$

        • $p$ konstanteko baldintzatan sistemak trukatu duen beroa da: $\delta Q=C_{p}dT$

        • Eta entropiaren eragiketa-definizioa kontuan hartuz: $dS=\frac{\delta Q}{T}\Rightarrow dS=\frac{C_{p}dT}{T}\Rightarrow {[dS=\frac{C_{p}dT}{T}]}_p$

        • Hauxe da ondorioa:

        $$\boxed{{\displaystyle {\left(\frac{\partial S}{\partial T}\right)}_p=\frac{C_p}{T}}}$$

  • Eta orokorrean…

    • $(T,X)$:

    $$\boxed{{\displaystyle {\left(\frac{\partial S}{\partial T}\right)}_X=\frac{C_X}{T}}}$$

    • $(T,Y)$:

    $$\boxed{{\displaystyle {\left(\frac{\partial S}{\partial T}\right)}_Y=\frac{C_Y}{T}}}$$

• Zenbait iruzkin:

  • Bero-iturriari dagokion entropia-aldaketa, definizioz: $dS=\frac{\delta Q_{b-i}^{IG}}{T_{b-i}}$

    1. Baina bero-iturriak beti trukatzen du bero era itzulgarrian (kuasiestatikoki, $\delta Q$, infinitesimala da kantitatea oso handia baita; eta energia barreiaketarik, horixe baita daukan askatasun-gradu bakarra, hots, ez dauka ezer energia barreiatzeko)

    2. Gainera, bero-iturriaren tenperatura beti da konstante, beraz, integraletik atera daiteke (horixe da, kasu honetan, ibilbidea ezagutzea, ibilbideko integrala, diferentzial ez-zehatz baten integrala kalkulatzeko)

  • Ondorioz:

    $$\boxed{{\displaystyle \mathrm{\Delta }{S}_{b-i}=\frac{Q_{bi-i}}{T_{b-i}}}}$$

  • kuasiestatikotasuna eta itzulgarritasuna:

    • definizioz ez dira berdinak: itzulgarriak kuasiestatiko dakar ondorioz, baina kontrara, ez!!

    • liburuko erabilera praktikoari dagokionez, badira berdinak: liburuaren arabera, kuasiestatiko izatean, azpitik, onartzen ari da itzulgarria dela baita ere

• Ariketa bat proposatu:

• Aztertu behar den sistemaren ezaugarriak honako hauek dira: $m$ eta $c$; hots, badakigu zer masakoa den eta nola trukatzen duen energia bero moduan eta masa unitateko.

  Bero-ahalmen horretan ez dago adierazita zer baldintza esperimentaletan trukatuko duen beroa sistemak, baina, berdin dio, onartuko da, trukea gertatuko den moduari dagokiola aipatutako bero-ahalmena.

• Kalkulatu honako hauek:

  1. Sistema eraman da 1-egoeratik, $T_1$ tenperaturakoa bera, 2-egoerara, $T_2$ tenperaturakoa bera. Prozesua bat-batean gertatu da.

     • Lortu:

       1. Unibertsoaren entropia-aldaketa: $\mathrm{\Delta }{S}^U$

       2. Sistemaren entropia-aldaketa: $\mathrm{\Delta }{S}^{sis}$

       3. Ingurunearen entropia-aldaketa: $\mathrm{\Delta }{S}^{ing}$

  • Jakina, horiek guztiek honako hau betetzen dute:

  $$\mathrm{\Delta }{S}^U=\mathrm{\Delta }{S}^{sis}+\mathrm{\Delta }{S}^{ing}$$

  • Onartu hasierako oreka-egoera lortzeko prozesua, hots, $T_1$ tenperaturan dagoen bero-iturriarekin ukipen termikoan jarritakoan gertatzen den prozesua dela prozesu osoaren parte.

  2. Sistema eraman da 1-egoeratik, $T_1$ tenperaturakoa bera, 2-egoerara, $T_2$ tenperaturakoa bera, bat-bateko bi azpi-prozesuren bidez eraman da, bi tenperaturen artean, erdiko tenperatura tartekatuz. Oraingo honetan ere bai kalkulatu behar dira aurrekoan kalkulatu behar izandakoak.

  3. Aurreko ariketa errepikatu, baina, oraingo honetan tarteko bi tenperatura tartekatuz, bestela, dena gertatzen da baldintza berberetan.

  4. … …

  5. …limitera eramanda, hasierako eta bukaerako egoeren artean, infinitu tenperatura tartekatu dira…

---

6.6 Bigarren Printzipioaren Ondorioak:

• metodo teknikoa:

  • Carnot-en zikloa*:

    

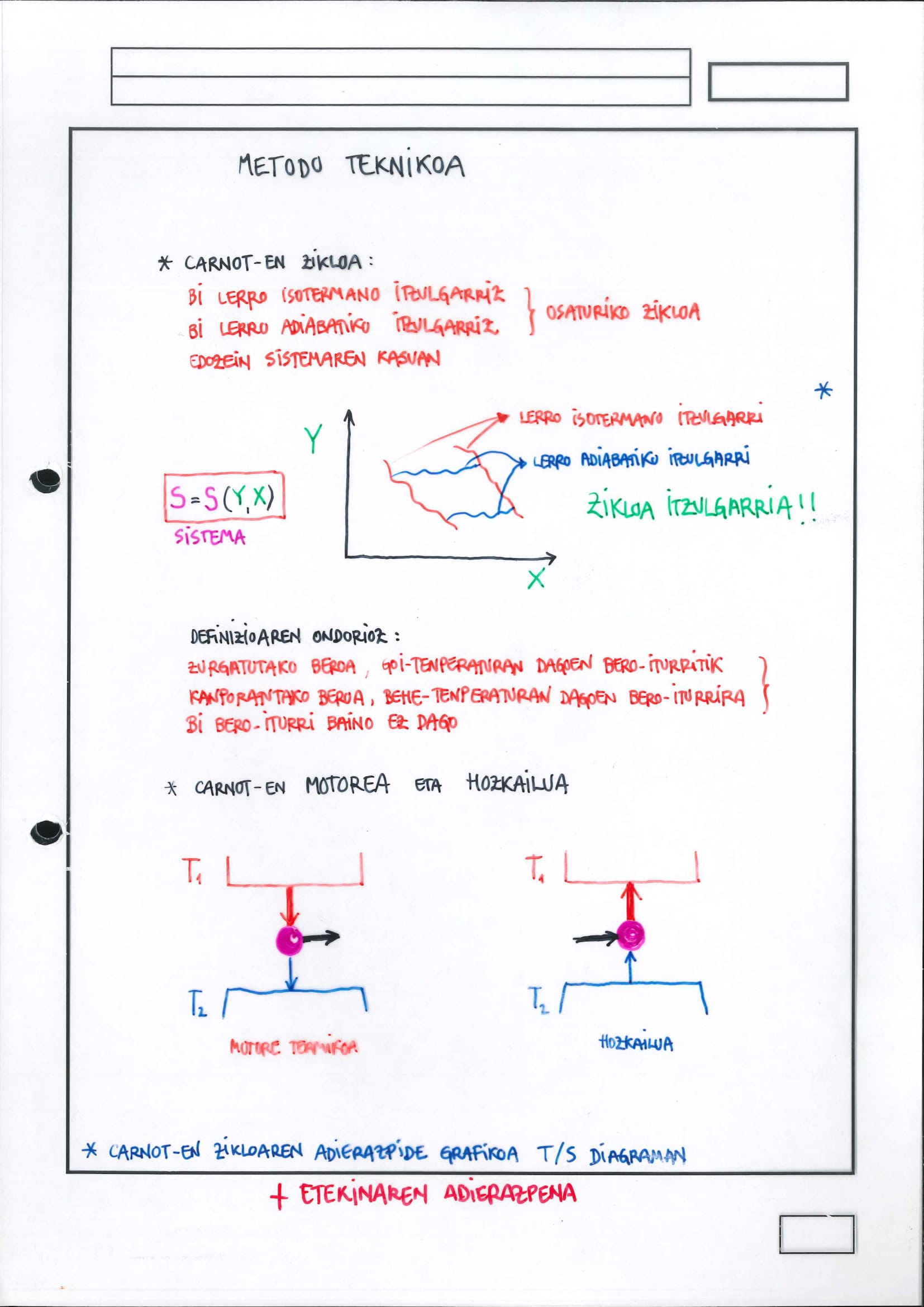
    • definizioa

    • iruzkinak/ezaugarriak:

      • Carnot-en zikloaren adierazpide grafikoa $(Y,X)$ diagrama orokorrean

      • Carnot-en zikloaren adierazpide grafikoa $(T,S)$ diagraman: unibertsala da, ez da behar ziklikoki bueltaka dabilen sistemari buruzko informaziorik

      • Ziklikoki dabilen sistema gas ideala da:

        • Carnot-en zikloaren adierazpide grafikoa $(p,V)$ diagraman

        • bestelako diagrametan: $(T,V)$, $(T,U)$, $(U,p)$, $\cdots$

      • Carnot-en zikloari dagokion etekina, makina termikoan erabilita zikloa eta makina termikoa motor termikoa denean (proposatutako ariketa):

      $$\boxed{{\displaystyle {\eta }_C=1-\frac{T_1}{T_0}}}$$

    • ezaugarriak: 2. Printzipioa erabilita ondorioztatutakoak

      • Carnot-en zikloaren etekinak ez dauka ziklikoki dabilen sistemarekiko mendekotasunik

      • Carnot-en zikloaren etekina maximoa da finkatutako bi tenperatura horien artean dabilen edozein motorri dagokionarekin alderatuta

4. Kelvin tenperatura-eskala:

   

Ariketa-proposamena

Clausius-en Teorema:

• Ez da frogatuko

5. Entropia-funtzioaren existentzia:

   

• Hauxe da bere eduki fisikoa:

  $$\oint \delta q_0=T_0\oint \frac{\delta q}{T}\le 0$$

• prozesua, zikloa, IG: $\oint \frac{\delta q}{T}=0$
  Gainera, berori erabil daiteke $S$ entropia-funtzioa ondorioztatzeko

  • Zikloko bi puntu aukeratu: $i$ eta $f$

  • Zikloa bera bi azpiprozesuz osatuta azter daiteke: $i\to f$ eta $f\to i$

  • Azpiprozesu bakoitzean $S$ kalkulatu daiteke:

    • $i\to f:{\int }_{i\to f}dS\equiv \mathrm{\Delta }{S}_{i\to f}=\boxed{{\displaystyle \mathrm{\Delta }{S}_{i-f}={{\int }_i^f}_a\frac{\delta q}{T}}}$

    • $f\to i:{\int }_{f\to i}dS\equiv \mathrm{\Delta }{S}_{f\to i}=\boxed{{\displaystyle \mathrm{\Delta }{S}_{f-i}={{\int }_f^i}_b\frac{\delta q}{T}}}$

  • $\mathrm{\Delta }{S}_{i\to f\to i}=\mathrm{\Delta }{S}_{i\to f}^a+\mathrm{\Delta }{S}_{f\to i}^b$

  • $\mathrm{\Delta }{S}_{i\to f\to i}=0$

  $$\mathrm{\Delta }{S}_{i\to f}^a+\mathrm{\Delta }{S}_{f\to i}^b=0\Rightarrow \mathrm{\Delta }{S}_{i\to f}^a=-\mathrm{\Delta }{S}_{f\to i}^b\Rightarrow \underset{\Downarrow {\int }_i^f\frac{\partial q}{T}}{\underbrace{\mathrm{\Delta }{S}_{i\to f}^a}}=\underset{\Downarrow {\int }_i^f\frac{{\delta }_q}{T}}{\underbrace{\mathrm{\Delta }{S}_{i\to f}^b}}$$

• prozesua, zikloa, IE: $\oint \frac{\delta q}{T}<0$

  Kasu honetan, $\frac{\delta q}{T}$ inoiz ez da entropia

6.7 Entropia-emendioaren Printzipioa

• Izadiko berezko prozesuetako entropia-aldaketaren kalkulua:

  

---

• Entropia-emendioaren frogapena, prozesu adiabatiko itzulezinetan:

  

$$\boxed{{\displaystyle \mathrm{\Delta }{S}^U\equiv \mathrm{\Delta }{S}^{ing}+\mathrm{\Delta }{S}^{sis}\ge 0}}$$

• Iruzkinak:

  1. 2 Printzipioak finkatzen du unibertsoaren entropia-aldaketaren zeinua

  2. 2 printzipioak finkatzen du unibertsoaren entropia-aldaketak izan dezakeen baliorik txikiena, zero!

  3. 2 Printzipioak ez du finkatzen ingurunearen eta sistemaren entropia-aldaketen balio erlatiboak: baturaren zeinua finkatuta dago, hori da baldintza murriztailea, baina, bestela, edozein konbinazio gerta daiteke (harekin bateragarri, jakina)

---

6.8 Lan Maximoaren Teorema

• Kualitatiboki:

  

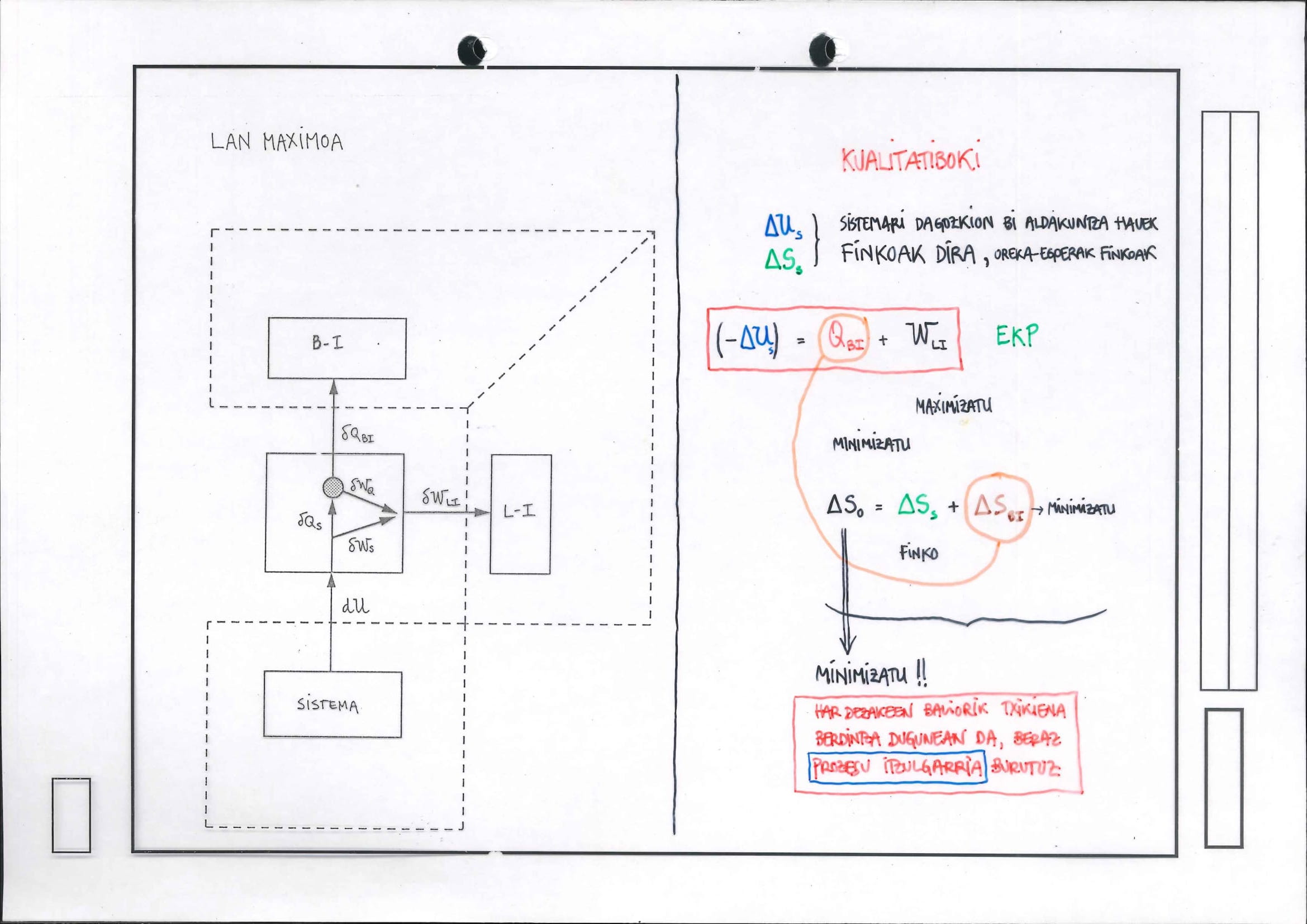
  • Helburua: Aztergai den sistemaren egoera-aldaketa jakina erabili nahi da lan maximoa (minimoa) lortzeko asmotan

  • Egoera-aldaketa jakina denez, norberak finkatutakoa esaterako eta sistemaren propietateak egoera-funtzioak direnez (diferentzial zehatzak), horien edozein aldaketa finkoa da

  • edozein gauza kalkulatzeko, 2 tresna baino ez dago, oraingoz:

    • lehen printzipioa: energiaren kontserbazioaren printzipioa

    • bigarren printzipioa: entropia-emendioaren forman, esaterako

  • gainera, bi tresnak unibertsoari dagozkie: unibertsoan aplikatu behar dira

    • hipotesiaren arabera, bi tresnetan sistemarekin lotutakoa finkatuta dago

• Kuantitatiboki (1):

  

  • Irudian adierazi nahi da eragingo den prozesua gertatzen den unibertsoaren inguruneak bi zati dauzka:

    • bero-iturri (itzulgarria): berak egin dezakeen gauza bakarra (duen askatasun-gradu bakarra) da energia bero moduan trukatzea

      • edozein prozesutan beti eragiten zaio entropia-aldaketa: $d{S}^{b-i}=\frac{\delta Q^{b-i}}{T^{b-i}}$

    • lan-iturri (itzulgarria): berak egin dezakeen gauza bakarra (duen askatasun-gradu bakarra) da energia lan moduan trukatzea

      • edozein prozesutan inoiz ez zaio eragiten entropia-aldaketa: $d{S}^{l-i}=0$

      • lan-iturri itzulgarriaren ikuspuntutik prozesu denak, itzulgarriak direnez (bere izaeraz), kuasiestatikoak dira baina adiabatikoak ere bai, ezin baitu, inolaz ere, beroa trukatu, ez baitauka askatasun-gradu termikorik

  • Unibertsoaren entropia-aldaketaren atalak dira

    1. sistemaren ekarpena

    2. ingurunetik, bero-iturri itzulgarriaren ekarpena Entropia-aldaketa osoak lotzen ditu bero-iturria eta sistema, azken honen entropia-aldaketaren bidez

  • Energia-truke osoari dagokionez, hots, unibertsoari dagokion energia-aldaketari dagokionez, eta energia kontserbatu behar denez (1. Printzipioa)

  Energiaren balantzeak lotzen ditu lan-iturria eta sistema, azken honen energia-aldaketaren bidez

• Kuantitatiboki (2):

  

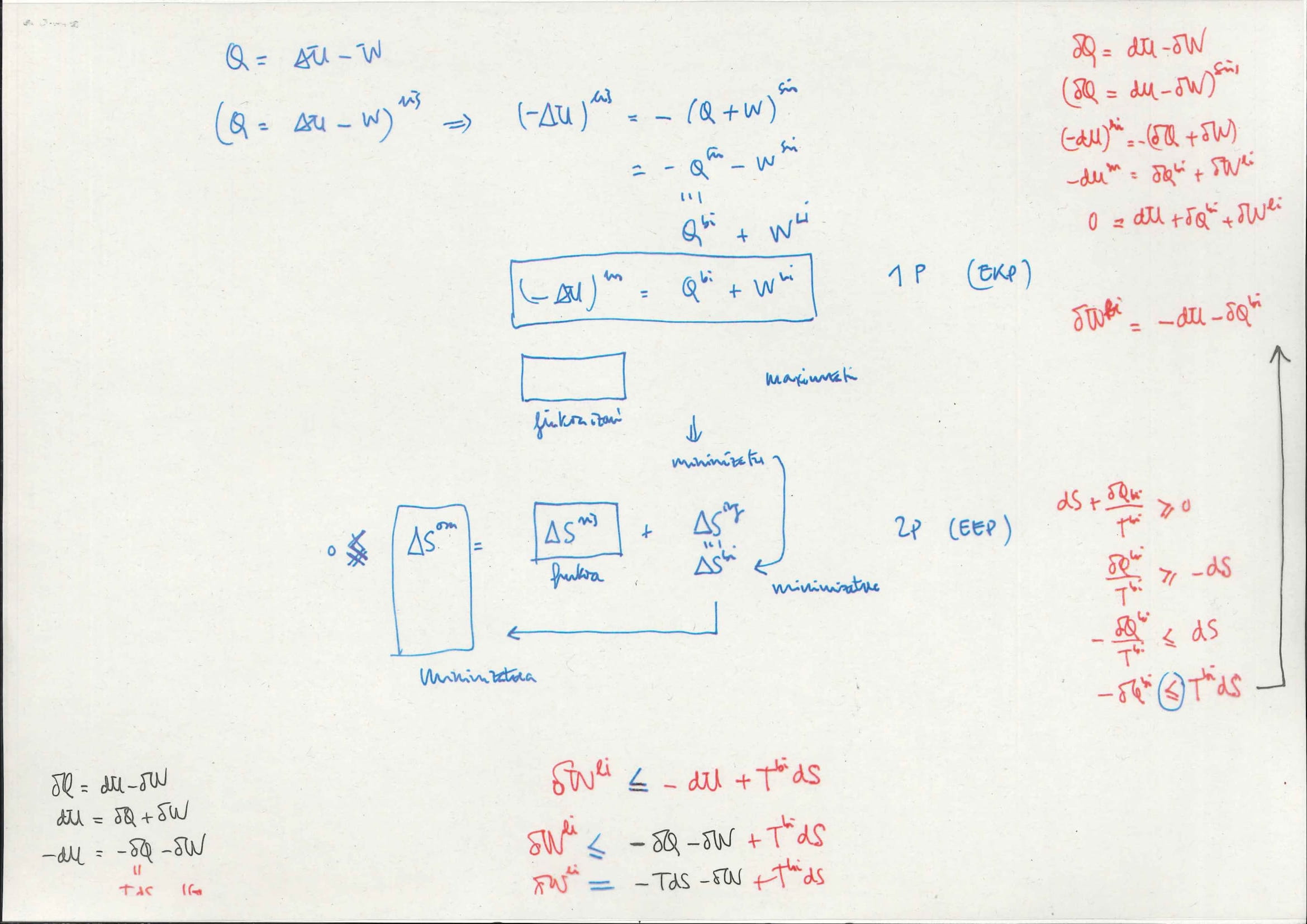
  • Azken adierazpenaren irakurketa: sistemaren egoera-aldaketa finkotik lor daitekeen lan maximoak 2 atal dauzka:

    $$\delta W^{l-i}=-\delta W-\left[TdS(1-\frac{T^{b-i}}{T})\right]$$

  • atalak:

    1. sistemak zuzenean emango duen lana: $\delta W$

       • lan horren izaera edozein izan daiteke, sistemaren askatasun-graduaren araberakoa: mekanikoa, magnetikoa, elektrikoa, elastikoa…

       • gehienetan onartuko da horrelako atalik ez dagoela

       • beraz, nahikoa izango da jakitea sistemak nola trukatzen duen energia bero moduan: sistemaren $C$ bero-ahalmena ezaguna izango da

    2. sistematik prozesuan zehar tenperatura-diferentziak gertatzen direnez, horiek erabiliz atera daitekeen lan maximoa

       horri dagokion adierazpena da Carnot-en makina termikoaren adierazpena: $\delta Q(1-\frac{T^{b-i}}{T})=TdS(1-\frac{T^{b-i}}{T})$

       • $\delta Q=TdS$ da sistemak $T$ tenperaturan trukatzen duen beroa
         $T$ tenperaturaren balioa aldatuz doa, sistema masa finitukoa baita

       • $(1-\frac{T^{b-i}}{T})$ da $(T^{b-i},T)$ tenperatura-diferentziarekin lotutako etekin maximoa, Carnot-en zikloari dagokiona, bi tenperatura horien arteko, sistemari dagokiona aldiunekoa da, aldatuz baitoa

• Kuantitatiboki (3):

  

• Adibideak:

  1. Ariketetako eskemak

  

1. Masa finituko bi sistemen arteko tenperatura-diferentzia aprobetxatu lana lortzeko

   

• Iruzkinak:

  • Bi sistemen arteko tenperatura-diferentzia

    • ez da aprobetxatu nahi, lana egiteko: prozesua da IE, berezkoa baita

      1. $\mathrm{\Delta }{U}^U=0\Rightarrow Q^U=0\Rightarrow \boxed{{\displaystyle Q^{sis,T_A}+Q^{sis,T_B}=0}}$

         • batak galtzen duen energia besteak irabazten du

         • horren arabera, sistema bakoitzaren kasuan, ${[Q=\mathrm{\Delta }U-W(=0)]}^i\Rightarrow {[Q=\mathrm{\Delta }U]}^i$

         • eta trukatutako beroa beti kalkulatu daiteke barne-energia kalkulatuz, diferentzial zehatza da bera

         • baldintza honek finkatzen du bukaerako egoera termikoa, beroa-ahalmenak ($c_A,c_B$) konstanteak badira $\boxed{{\displaystyle T_f^{IE}=\frac{m_A{c}_A{T}_i^A+m_B{c}_B{T}_i^B}{m_A{c}_A+m_B{c}_B}}}$

      2. Hori lortutakoan, kalkulatu daiteke zenbatekoa izan den entropia-aldaketa

         • $\mathrm{\Delta }{S}^j=\underset{T_i^j}{\overset{T_f^{IE}}{\int }}\frac{m_j{c}_j}{T_A}dT,(j=A,B)\Rightarrow \mathrm{\Delta }{S}^U=\underset{T_i^A}{\overset{T_f^{IE}}{\int }}\frac{m_A{c}_A}{T_A}d{T}_A+\underset{T_i^B}{\overset{T_f^{IE}}{\int }}\frac{m_B{c}_B}{T_B}d{T}_B$

         • ($T_A,T_B$) aldagai mutuak dira, aldatuz doaz, masa finituko sistemak baitira

    • aprobetxatu nahi da, lana egiteko:

      1. $Q^U\equiv Q^A+Q^B=-W$, aljebraikoa, zeinua beroetan sartuta dago

         • onartuko da sistemek ez dutela lana zuzenean kanporatzen (edo ez dutela kontsumituko lanik, ez dela sartuko)

         • oraingoan, batak galdutako beroa ez da besteak irabazten duena: bero-trukea modu berezian eragin behar da, zeinean unibertsoaren entropia-aldaketa ez den aldatzen, guztira, baina edozein azpi-prozesu infinitesimaletan ere ez

      2. $d{S}^U=0\Rightarrow d{S}^U=d{S}^A+d{S}^B\Rightarrow 0=d{S}^A+d{S}^B\Rightarrow \boxed{{\displaystyle d{S}^B=-d{S}^B}}$

         • bi sistemen artean gertatzen den bero-trukea oso berezia da: entropia kontserbatzen baitu, horretarako tartekatu den zerbaiten bidez, jakina

         • baldintza horrek finkatzen du bukaerako egoera termikoa, bero-ahalmenak ($c_A$, $c_B$) konstanteak badira $\boxed{{\displaystyle T_f^{IG}={[(T_i^A{)}^{m_A{c}_A}(T_i^B{)}^{m_B{c}_B}]}^{\frac{1}{m_A{c}_A+m_B{c}_B}}}}$

  • Lan minimoko edozein problema, lan maximoko problemaren berdina da, kontrako noranzkokoan eraginda

    • Lan maximoa lortzeko eragin beharreko prozesuak itzulgarri izan behar du; beraz, beti bete daiteke kontrako noranzkoan

    • Lan minimoaren probleman honako hau eskatzen da (gehienetan, problemaren aldaerak ere badaude): zenbatekoa den egin behar den lana tenperatura berean dauden bi sistemen artean tenperatura-diferentzia jakina eragiteko

    • Hasierako egoeran, bi sistemen egoera termikoak berdinak dira: $T_i^{min}=T_f^{max}$ Bukaerako egoeran, sistemen artean tenperatura-diferentzia dago: $T_f^{min}=T_i^{max}$

    • Batean zein bestean lortuko diren lanen balio absolutuak berdinak dira

      • maximoa eta minimoa estremalak dira (inflexio-puntuarekin batera) eta lehen deribatuak berak ez daki zein den zein, aipatutako hirurek betetzen baitute baldintza berbera lehen deribatuari dagokionez: nulua da

      • Eta berori da erabili den baldintza bakarra: prozesua itzulgarria denez, unibertsoaren entropia-aldaketa nulua da, baina edozein azpi-prozesu infinitesimaletan, beraz, beti betetzen da $d{S}^U=0$ (lehen deribatua!)

• 6.8 Lan Maximoaren Teoremaren adibideak

  • Adibideak:

    1. Problema moten eskemak

    

    2. Masa finituko bi sistemen arteko tenperatura-diferentzia aprobetxatu lana lortzeko

    

    3. Masa finituko sistema eta bero-iturriaren arteko tenperatura-diferentzia aprobetxatu lana lortzeko

    

  • Bi zalantza argitu:

    1. Besterik gabe lotutakoan masa finituko bi sistema, zergatik kalkulatu daiteke beroa (diferentzial zehatza ez dena) prozesua itzulgarria izango balitz moduan, nahiz eta itzulezina den?

       • Ikus gorago

    2. Zer gertatzen da, aipatutako edozein prozesutan, bereziki, masa finituko sistema eta bero-iturria besterik gabe lotzean, masa finituko sistemaren masa bera ere aldatzen bada? Mahai gainean utzitako egin berri den kafez betetako potoari gertatzen zaion prozesua

       • Pentsatzeko

• Ariketa proposatu: 27. ariketa

Esku artean $C_V$ bero-ahalmeneko $N$ sistema berdin ditugu; beren tenperaturak $\{T_1,T_2,\dots T_N\}$ dira.

1. Besterik gabe, elkarren arteko ukipen termikoan jarri dira. Zenbatekoa da trukatu duten bero kantitate osoa?

2. Demagun, ondoren, $T_0$ tenperaturan dagoen bero-iturria erabilgarri dela eta horrekin ukipen termikoan jarri direla sistemak. Zenbatekoa da horrelako egoeratik atera daitekeen lan maximoa?

Jakina, lortu sistemen bukaerako oreka-egoera termikoa, arestian aipatutako bi kasuetan.

• Proposatutako ariketa egin:

  • Nahiz eta kasu honetan $N$ sistema izan, aurreko kasuetan bi sistema baino ez da aztertu, bi lotze modutan: besterik gabe prozesu IEaren bidez, bi sistemen artean dagoen tenperatura-diferentzia lan egitearen ikuspuntutik aprobetxatzeko asmotan, lana maximizatuz, gainera, IGaren bidez lotuta, hortaz, ebazpen-protokoloa ez da aldatzen; hots, aurreko kasuan egin den berbera egin behar da:

    1. besterik gabe lotuz gero: prozesua da IEa:

       1. EKParen (1. Printzipioa) ekuazioak finkatuko du zein den bukaerako orekako egoera termikoa, bukaerako tenperatura: $T_f^{IE}$

       $$\boxed{{\displaystyle T_f^{IE}=\frac{\sum _{j=1}^N{C}_V^j{T}_i^j}{\sum _{j=1}^N{C}_V^j}}}$$

       2. EEParen (2. printzipioa) ekuazioak finkatuko du zein den unibertsoaren entropia-aldaketa, positiboa bera:

       $$\mathrm{\Delta }{S}^j=\underset{T_i^j}{\overset{T_f^{IE}}{\int }}\frac{C_V^j}{T^j}d{T}^j,(j=1,\dots ,N)\Rightarrow \boxed{{\displaystyle \mathrm{\Delta }{S}^U=\sum _{j=1}^N\left[\underset{T_i^j}{\overset{T_f^{IE}}{\int }}\frac{C_V^j}{T^j}d{T}^j\right]}}$$

    2. lana egiteko asmoz lotuz eta, gainera, lana maximoa izateko: prozesua da IGa:

       1. EKParen (1. Printzipioa) ekuazioak finkatuko du zenbatekoa den aterako den lan maximoa: $$Q^U\equiv \sum _{j=1}^N{Q}^j=-W^{max}$$$$Q^j=\underset{T_i^j}{\overset{T_f^{IE}}{\int }}{C}_V^{j}d{T}^j,(j=1,\dots ,N)$$

       2. EEParen (2. printzipioa) ekuazioak finkatuko du zein den bukaerako orekako egoera termikoa, bukaerako tenperatura: $T_f^{IG}$

       $$\boxed{{\displaystyle T_f^{IG}={[\prod _{j=1}^N(T_i^j{)}^{C_V^j}]}^{\frac{1}{\sum _{j=1}^N{C}_V^j}}}}$$

• 6.9 Energia ez-erabilgarria (galdutako energia?)

  • Kontzeptua eta kalkuluaren adibide erraza:

    

  • Frogapena

    

  • Energiaren kalitatea: Orokortzea; zuok irakurri eta hausnartu

    

  • Iruzkinak:

    • Iraganerako mehatzatzea: ordenaren bila

    • Ez dauka zentzurik energia aurrezteak; printzipioz (lehenengo printzipioz), ez da ezer egin behar energia aurrezteko, berez, aurrezten da, kontserbatzen baita. Beste kontu bat da kontserbatzen den energia hori lan egiteko erabili nahi izatea…, horren kasuan, bigarren printzipioak hartzen du parte; haren ondorio bat, entropia bera, erabil daiteke kalitate handiko energia aurreztu behar dela esateko, beti ere, helburua lan egitea bada. Hots, askoz hobea da, errentagarriago lan egitearen ikuspuntutik, entropia txikiko energia erabiltzea lan egiteko entropia handiko energia baino

---

• Ariketa kualitatiboak:

• Ariketa proposatu, pentsatzen joateko…: 15. ariketa

  • 

• Ariketak: 14. ariketa

  • Gas ideal monoatomiko baten $n$ molei konpresio kuasiestatikoa eragin diegu, $m$ masako likidoarekin ukipen diatermoan daudela. Horrela, gasaren tenperatura aldatu da. Likidoaren presioak konstante iraungo du eta bere bero-ahalmena $c_{pl}$ da. Gasaren hasierako eta bukaerako bolumenak $V_A$ eta $V_B$ dira, hurrenez hurren; eta gasaren eta likidoaren hasierako eta bukaerako tenperaturak $T_A$ eta $T_B$. Lortu honako hauek:

    1. Likidoak xurgatu duen beroa.

    2. Gasaren entropia-aldaketa eta barne-energiaren aldaketa.

    3. Gasak egindako lana.

    4. Frogatu $A\to B$ prozesuak honako ekuazio honi segitzen diola: $T{V}^{a-1}=C$

    5. Lortu $a$ konstantearen balioa eta, berebat, lortu $a$ konstantearen limitea honako bi kasu hauetan:

    • $m{c}_{pl}\to 0$

    • $m{c}_{pl}\to \mathrm{\infty }$

    • Zer motatako transformazio izango da prozesua bi kasu limiteetan?

• Ariketak: 17. ariketa

  • Esku artean gas ideal baten 1 mol-eko lagina dugu. 25 ${}^{\circ }$ C-an dagoen bero-iturriarekin ukipenean dagoela, 100 atm-tik 1 atm-erako espantsioa eragin diogu laginari. Lortu unibertsoaren entropia-aldaketa honako bi kasu hauetan:

    1. Lanik egin ez bada.

    2. Egindako lana 2980 joule izan bada.

• Ariketak: 18. ariketa

  • Bereizte-horma diatermoak eta higikorrak $V_A$ eta $V_B$ hasierako bolumeneko bi guneetan banatu ditu. Guneek gas ideal baten mol bana dute eta hasierako egoera berean daude: $T$ tenperaturako egoera termikoan. Frogatu, bukaerako oreka-egoera lortutakoan, guneei (sistema konposatu moduan) dagokien entropia-aldaketa ondoko hau dela:

    $$\mathrm{\Delta }S=R\ln \left\{\frac{(V_A+V_B{)}^2}{4V_A{V}_B}\right\}$$

• Ariketak: 20. ariketa

  • Esku artean dugun hari elastikoa $1.5L_0$ luzera lortu arte luzatu dugu, era itzulgarrian. $L_0$ da hasierako luzera. Inguruneko tenperatura 27 ${}^{\circ }$ C da eta, aipatutako prozesuan, hariak 1000 J xurgatu du, ingurunetik. Luzapenaren ondoren, hari elastikoa askatu dugu eta hasierako luzera berreskuratu du, era itzulgarrian. Azken prozesu horretan 2600 J-ko lana egin du sistemak. Lortu honako hauek:

    1. Hariaren entropia-aldaketa, luzatutakoan.

    2. Hariaren entropia-aldaketa, bigarren prozesuaren ondorioz.

    3. Unibertsoaren entropia-aldaketa, bi prozesuen ondorioz.

    4. Luzapenean egindako lana.

• Ariketak: 21. ariketa

  • Aztertu beharreko gas erreala era askean zabaldu da, $T=300$ K-eko bero-iturriarekin ukipen termikoan. Prozesu horretan xurgatu duen beroa da $Q=50$ J. Lehenengo prozesu horren ondoren, gasa konprimitu dugu, era isotermo itzulgarrian; hasierako egoera berreskuratu arte. Bigarren prozesu horretan, gasak 300 J kanporatu du. Lortu honako hauek:

    1. Gasaren entropia-aldaketa, lehenengo prozesuan.

    2. Gasak egindako lana, bigarren prozesuan.

• Aste honetan egindako ariketak

Ariketak: 2. Printzipioarekin lotutakoak, honako hauek

1. 12. Ariketa

2. 16. Ariketa

3. 17. Ariketa

4. 27. Ariketa