Ariketak

---

Oinarrizko ekuazioaren eraikuntza

Zenbait ariketa, adibide

Kontuz ibili behar da oinarrizko ekuazioa eraiki behar denean egoera-ekuazioetatik abiatuta. Oinarrizko ekuazioaren zer forma, energetikoa edo entropikoa, lortu(behar)ko dugun, egoera-ekuazioek esango digute. Beraz, ondo erreparatu egoera-ekuazioetan agertzen diren aldagai naturalei, hortxe baitago gakoa.

Hurrengo sei ariketetan, lortu oinarrizko ekuazioa. Kontuan izan sistema denak hidrostatikoak direla, baina bina egoera-ekuazio baino ez dela ezagutzen enuntziatuetan.

Testuingurua

1. ARIKETA

$$T=3A\frac{s^2}{v}$$

$$p=A\frac{s^3}{v^2}$$

Emaitza

$U=A\frac{S^3}{V}\frac{1}{N}+N\cdot k$

$\mu =-A\frac{s^3}{v}+k$

Ebazpen posible bat…

---

Testuingurua

2. ARIKETA

$$U=PV$$

$$P=B{T}^2$$

Emaitza

$d\left(\frac{\mu }{T}\right)=0\Rightarrow \left(\frac{\mu }{T}\right)=k\Rightarrow \left(\frac{\mu }{T}\right)={\left(\frac{\mu }{T}\right)}_0$

$S=2B^{\frac{1}{2}}{V}^{\frac{1}{2}}{U}^{\frac{1}{2}}-{\left(\frac{\mu }{T}\right)}_{0}N$

Ebazpen posible bat…

---

Testuingurua

3. ARIKETA

$$u=\frac{3}{2}pv$$

$$u^{\frac{1}{2}}=BT{v}^{\frac{1}{3}}$$

Emaitza

$\left(\frac{\mu }{T}\right)=-\frac{1}{3}B{v}^{\frac{1}{3}}{u}^{\frac{1}{2}}$

$S=2B{V}^{\frac{1}{3}}{U}^{\frac{1}{2}}{N}^{\frac{1}{6}}+N{s}_0$

Ebazpen posible bat…

$$\begin{array}{r}\begin{array}{rcclccl}du& =& T& ds& +& p& dv\\ du& =& \frac{3A{s}^2}{v}& ds& -& \frac{A{s}^3}{v^2}& dv\\ \\ \int du\equiv u& =& \int \frac{3A{s}^2}{v}& ds& +& f(v)& \end{array}\end{array}$$

$$du=\int \frac{3A{s}^2}{v}ds+f(v)\Rightarrow {\left(\frac{\partial u}{\partial v}\right)}_s=-\frac{A{s}^3}{v^2}+f^{\prime }(v)\Rightarrow$$

$$\begin{array}{r}\cancel{-\frac{A{s}^3}{v^2}}+f^{\prime }(v)=\cancel{-\frac{A{s}^3}{v^2}}\\ \Rightarrow f^{\prime }(v)=0\Rightarrow f(v)=\text{ ktea }\end{array}$$

$$\boxed{{\displaystyle u=\frac{A{s}^3}{v}+\text{ ktea }}}$$

$$\begin{array}{r}\begin{array}{rcc}u\equiv \frac{U}{N}& =& A\frac{{\left(S/N\right)}^3}{\left(V/N\right)}+N\cdot \text{ktea}\Rightarrow \\ U& =& A\frac{S^3}{N^{\cancel{3}}}\frac{\cancel{N}}{V}\cancel{N}+N\cdot \text{ktea}\Rightarrow \end{array}\end{array}$$

$$\boxed{{\displaystyle U=A\frac{S^3}{VN}+N\cdot \text{ktea}}}$$

$${\left[dp\right]}_U=\underbrace{{\left(\frac{\partial p}{\partial T}\right)}_U}\frac{pV\alpha -C_p}{V(-T\alpha +p{\kappa }_T)}{\left[dT\right]}_U(\equiv {\left(\frac{\partial T}{\partial V}\right)}_{U}dV)$$

---

Testuingurua

4. ARIKETA

$$U=\frac{1}{2}PV$$

$$T^2=A\frac{U^{\frac{3}{2}}}{V{N}^{\frac{1}{2}}}$$

Emaitza

$\left(\frac{\mu }{T}\right)=-A^{-\frac{1}{2}}{v}^{\frac{1}{2}}{u}^{\frac{1}{4}}$

$S=4A^{-\frac{1}{2}}{U}^{\frac{1}{4}}{V}^{\frac{1}{2}}{N}^{\frac{1}{4}}+S_0$

Ebazpen posible bat…

---

Testuingurua

5. ARIKETA

Gas ideala

Emaitza

Gas ideala monoatomikoa da; ez da orokortasunik galtzen.

$PV=NRT$

$U=\frac{3}{2}NRT$

Ebazpen posible bat…

---

Testuingurua

6. ARIKETA

Van der Waals-en jariakina

Emaitza

$\frac{1}{T}=\frac{cR}{(u+\frac{a}{v})}$

$\frac{P}{T}=\frac{R}{v-b}-\frac{acR}{(u{v}^2+av)}$

$\boxed{{\displaystyle S=NR\ln \left[(v-b){(u+\frac{a}{v})}^c\right]+N{s}_0}}$

Ebazpen posible bat…

---

Oinarrizko ekuazioaren propietateak eta gehiago…

Testuingurua

7. ARIKETA

Zenbait sistema termodinamikori dagokion oinarrizko ekuazioa agertuko da ondoren. Dena den, horietariko bost, II, III eta IV postulatuetatik baten edo gehiagoren aurka dago; eta, ondorioz, fisikoki onartezinak dira.

Adieraz itzazu aipatu bostak, eta betegabeko postulatua(k). Adierazpen horietan guztietan, $v_0$, $\theta$ eta $R$ konstante positiboak dira.

Onartu erro positibo erreala soilik, berretura frakzionarioa ageri den guztietan.

1. $S={\left({\displaystyle \frac{R^2}{v_0\theta }}\right)}^{\frac{1}{3}}{\left[NVU\right]}^{\frac{1}{3}}$

2. $S={\left({\displaystyle \frac{R}{{\theta }^2}}\right)}^{\frac{1}{3}}{\left[{\displaystyle \frac{NU}{V}}\right]}^{\frac{2}{3}}$

3. $S={\left({\displaystyle \frac{R}{\theta }}\right)}^{\frac{1}{2}}{[NU-{\displaystyle \frac{R\theta V^2}{v_0^2}}]}^{\frac{1}{2}}$

4. $S=\left({\displaystyle \frac{R^2\theta }{v_0^3}}\right){\displaystyle \frac{V^3}{NU}}$

5. $S={\left({\displaystyle \frac{R^3}{v_0{\theta }^2}}\right)}^{\frac{1}{5}}{\left[N^{2}V{U}^2\right]}^{\frac{1}{5}}$

6. $S=NR\ln \left({\displaystyle \frac{UV}{N^{2}R\theta v_0}}\right)$

7. $S={\left({\displaystyle \frac{R}{\theta }}\right)}^{\frac{1}{2}}{\left[NU\right]}^{\frac{1}{2}}\exp (-{\displaystyle \frac{V^2}{2N^2{v}_0^2}})$

8. $S={\left({\displaystyle \frac{R}{\theta }}\right)}^{\frac{1}{2}}{\left[NU\right]}^{\frac{1}{2}}\exp (-{\displaystyle \frac{UV}{NR\theta v_0}})$

9. $U=\left({\displaystyle \frac{v_0\theta }{R}}\right){\displaystyle \frac{S^2}{V}}\exp \left({\displaystyle \frac{S}{NR}}\right)$

10. $U=\left({\displaystyle \frac{R\theta }{v_0}}\right)NV(1+{\displaystyle \frac{S}{NR}})\exp (-{\displaystyle \frac{S}{NR}})$

(C 1.9.1)

Emaitza

Ebazpen posible bat…

---

Testuingurua

8. ARIKETA

Lortu $U$ barne-energia $S$, $V$ eta $N$ aldagaien funtzioan, aurreko ariketako fisikoki onargarriak diren oinarrizko ekuazioen kasuetarako.

(C 1.9.2)

Emaitza

Ebazpen posible bat…

---

Testuingurua

9. ARIKETA

$A$ sistemaren oinarrizko ekuazioa honako hau da:

$$S_A={\left(\frac{R^2}{v_0\theta }\right)}^{\frac{1}{3}}{\left[N_A{V}_A{U}_A\right]}^{\frac{1}{3}}$$

$B$ sistemarena, berriz:

$$S_B={\left(\frac{R^2}{v_0\theta }\right)}^{\frac{1}{3}}{\left[N_B{V}_B{U}_B\right]}^{\frac{1}{3}}$$

Lortu $A+B$ sistema konposatuaren oinarrizko ekuazioa

(C 1.9.3)

Emaitza

Ebazpen posible bat…

---

Testuingurua

10. ARIKETA

Onartu aurreko ariketan deskribatutako $A$ eta $B$ azpisistemen arteko bereizte-horma finkoa, iragaztezina eta energia trukatzen utziko duena dela. Modu berean, demagun $A$ sistemaren bolumena $3$ cm${}^3$ dela, eta mol-kopurua 3. $B$ sistemaren kasuan, bolumena $4$ cm${}^3$ da eta mol-kopurua, $2$.

Sistema konposatuaren energia osoa $20$ cal da.

1. Adieraz ezazu entropia $A$ sistemari dagokion $\frac{U_A}{(U_A+U_B)}$ energia-frakzioaren funtzioan.

2. Zenbatekoa da azpisistema bakoitzari dagokion barne-energia sistemak oreka lortu duen kasurako?

(C 1.9.4)

Emaitza

Ebazpen posible bat…

---

Testuingurua

11. ARIKETA

Lortu ondoko oinarrizko ekuazioko sistemari dagozkion hiru egoera-ekuazioak:

$$U=\left(\frac{v_0\theta }{R^2}\right)\frac{S^3}{NV}$$

(C 2.2.1)

Emaitza

Ebazpen posible bat…

$U=\left(\frac{v_0\theta }{R^2}\right)\frac{S^3}{NV}\Rightarrow U=C\cdot \frac{S^3}{NV}U=U(S,V,N)$

$$\begin{array}{r}\{\begin{array}{rl}T& \equiv {\left(\frac{\partial U}{\partial S}\right)}_{V,N}\Rightarrow T=\frac{3C{S}^2}{NV}\\ -p& \equiv {\left(\frac{\partial U}{\partial V}\right)}_{S,N}\Rightarrow -p=-\frac{C{S}^3}{N{V}^2}\Rightarrow p=C\frac{S^3}{N{V}^2}\\ \mu & \equiv {\left(\frac{\partial U}{\partial N}\right)}_{S,V}\Rightarrow \mu =-\frac{C{S}^3}{N^{2}V}\end{array}\end{array}$$

---

Testuingurua

12. ARIKETA

Lortu aurreko sistemari dagokion $\mu$ potentzial kimikoa.

Adieraz ezazu emaitza $T$, $V$ eta $N$ parametroen funtzioan.

(C 2.2.2)

Emaitza

Ebazpen posible bat…

$\mu =\mu (T,V,N)$

$T=3C\frac{S^2}{NV}\Rightarrow S={\left(\frac{1}{3}\frac{NVT}{C}\right)}^{\frac{1}{2}}$

$\mu =-C\frac{S^3}{N^{2}V}\Rightarrow \mu =-C\frac{1}{N^{2}V}\cdot {\left(\frac{1}{3}\frac{NVT}{C}\right)}^{\frac{3}{2}}$

$\mu =-\frac{C}{C^{\frac{3}{2}}}\cdot \frac{T^{\frac{3}{2}2}{N}^{\frac{3}{2}}{V}^{\frac{3}{2}}}{N^2\cdot V}{\left(\frac{1}{3}\right)}^{\frac{3}{2}}$

$\mu =-{\left(\frac{1}{3}\right)}^{\frac{3}{2}}{C}^{-\frac{1}{2}}\frac{1}{N^{\frac{1}{2}}}{V}^{\frac{1}{2}}\cdot T^{\frac{3}{2}}$

---

Testuingurua

13. ARIKETA

Lortu aurreko sistemaren kasuan, eta tenperatura finkoa denean, presioak bolumenarekiko duen mendekotasuna, hautazkoa den eskalako diagraman.

Irudikatu bi tenperatura desberdini dagozkien lerro isotermoak, eta adieraz ezazu zein den bietatik tenperatura handienari dagokiona.

(C 2.2.3)

Emaitza

Ebazpen posible bat…

$p=p(T,V)$

$T=3C\frac{S^2}{NV}\Rightarrow S=\frac{1}{3}{\left(\frac{NVT}{C}\right)}^{\frac{1}{2}}$

$p=C\frac{S^3}{N{V}^2}\downarrow p=C\frac{1}{N{V}^2}{\left(\frac{NVT}{C}\right)}^{\frac{3}{2}}\Rightarrow p=\frac{1}{C^{\frac{1}{2}}}\cdot N^{\frac{3}{2}-1}{V}^{\frac{3}{2}-2}{T}^{\frac{3}{2}}$

$\begin{array}{rl}& p=\frac{1}{C^{\frac{1}{2}}}\frac{N^{\frac{1}{2}}}{W^{\frac{1}{2}}}\cdot T^{\frac{3}{2}}\\ & T=K\\ & N=K\end{array}$

$p=\frac{N^{\frac{1}{2}}\cdot \frac{1}{C}}{v^{\frac{3}{2}}}$

$p\cdot V^{\frac{3}{2}}=K$

---

Testuingurua

14. ARIKETA

Lortu ondoko oinarrizko ekuazioko sistemari dagozkion hiru egoera-ekuazioak.

$$u=\left(\frac{\theta }{R}\right)s^2-\left(\frac{R\theta }{v_0^2}\right)v^2$$

(C 2.2.4)

Emaitza

Ebazpen posible bat…

---

Testuingurua

15. ARIKETA

Lortu aurreko sistemari dagokion $\mu$ potentzial kimikoa; adieraz ezazu emaitza $T$ eta $p$ parametroen funtzioan.

(C 2.2.5)

Emaitza

Ebazpen posible bat…

---

Testuingurua

16. ARIKETA

Lortu ondoko oinarrizko ekuazioko sistemari dagozkion hiru egoera-ekuazioak.

$$u=\left(\frac{v_0\theta }{R}\right)\frac{s^2}{v}\exp \left(\frac{s}{R}\right)$$

(C 2.2.6)

Emaitza

Ebazpen posible bat…

---

Testuingurua

17. ARIKETA

kuasiestatikoa den zabaltze adiabatikoan zehar ($dS=0$), tenperaturak bolumenarekiko duen mendekotasuna.

(C 2.2.7)

Emaitza

Ebazpen posible bat…

---

Testuingurua

18. ARIKETA

Lortu, adierazpen entropikoan, ondoko oinarrizko ekuazioko sistemari dagozkion hiru egoera-ekuazioak.

$$u=\left(\frac{v_o^{\frac{1}{2}}\theta }{R^{\frac{3}{2}}}\right)\frac{s^{\frac{5}{2}}}{v^{\frac{1}{2}}}$$

(C 2.3.1)

Emaitza

Ebazpen posible bat…

---

Testuingurua

19. ARIKETA

Lortu aurreko sistemaren kasuan, eta presioa finkoa den kasuan, tenperaturak bolumenarekiko duen mendekotasuna, hautazkoa den eskalako diagraman.

Irudikatu bi presio desberdini dagozkien lerro isobaroak, eta adierazi zein den bietatik presio handienari dagokiona.

(C 2.3.2)

Emaitza

Ebazpen posible bat…

---

Testuingurua

20. ARIKETA

Lortu, adierazpen entropikoan, ondoko oinarrizko ekuazioko sistemari dagozkion hiru egoera-ekuazioak:

$$u=\left(\frac{\theta }{R}\right)s^2\exp \left(\frac{v^2}{v_0^2}\right)$$

(C 2.3.3)

Emaitza

Ebazpen posible bat…

---

Testuingurua

21. ARIKETA

Bi osagaiko sistemari dagokion oinarrizko ekuazioa honako hau da,

$$S=NA+NR\ln \left(\frac{U^{\frac{3}{2}}V}{N^{\frac{5}{2}}}\right)-N_{1}R\ln \left(\frac{N_1}{N}\right)-N_{2}R\ln \left(\frac{N_2}{N}\right)$$

$$N\equiv N_1+N_2$$

Adierazpen horretan $R=1.986$ cal/mol K da, eta $A$, finkatu gabeko konstantea.

Lehenengo osagaiarekiko iragazkorra baina bigarrenarekiko ez den mintz diatermoak bi gunetan zatitu du $10$ $\mathcal{l}$-ko bolumeneko eta itxita dagoen zilindro zurruna.

1. Lehenengo gunean ondoko parametroez ezaugarritutako lagina kokatu da: $N_1^{(1)}=0.5$, $N_2^{(1)}=0.75$, $V^{(1)}=5$ l eta $T^{(1)}=300$ K.

2. Bigarrenean, berriz, ondokoen bidez: $N_1^{(2)}=1$, $N_2^{(2)}=0.5$, $V^{(2)}=5$ l eta $T^{(2)}=250$ K.

Oreka lortutakoan, zein dira $N_1^{(1)}$, $N_1^{(2)}$, $T$, $p^{(1)}$ eta $p^{(2)}$ parametroen balioak?

(C 2.8.1)

Emaitza

Ebazpen posible bat…

• $$\begin{array}{r}\begin{array}{l}S=NA+NR\ln \left[\frac{U^{\frac{3}{2}}V}{N^{\frac{5}{2}}}\right]-N_{1}R\ln \left[\frac{N_1}{N}\right]-N_{2}R\ln \left[\frac{N_2}{N}\right]\\ N=N_1+N_2\\ \\ \frac{1}{T}={\left(\frac{\partial S}{\partial U}\right)}_{V,N_1,N_2}\Rightarrow \frac{1}{T}=NR\frac{3}{2}\frac{1}{U}\\ \\ \frac{p}{T}={\left(\frac{\partial U}{\partial V}\right)}_{S,N_1,N_2}\Rightarrow \frac{p}{T}=NR\frac{1}{V}\\ \\ \frac{{\mu }_1}{T}=-{\left(\frac{\partial U}{\partial N_1}\right)}_{S,V,N_2}\Rightarrow \frac{{\mu }_1}{T}=-A+\frac{5}{2}R-R\ln \left[\frac{U^{\frac{3}{2}}V}{N^{\frac{3}{2}}{N}_1}\right]\\ \\ \frac{{\mu }_2}{T}=-{\left(\frac{\partial U}{\partial N_2}\right)}_{S,V,N_1}\Rightarrow \frac{{\mu }_2}{T}=-A+\frac{5}{2}R-R\ln \left[\frac{U^{\frac{3}{2}}V}{N^{\frac{3}{2}}{N}_2}\right]\\ \\ \end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}{\left\{\begin{array}{c}S=NA+NR\ln \left[\frac{U^{\frac{3}{2}}V}{N^{\frac{5}{2}}}\right]-N_{1}R\ln \left[\frac{N_1}{N}\right]-N_{2}R\ln \left[\frac{N_2}{N}\right]\\ \\ N=N_1+N_2\\ U=U_1+U_2\end{array}\right\}}^{\left(i\right)}i=1,2\Rightarrow \\ \\ \begin{array}{c}{S}^{\left(i\right)}=N^{\left(i\right)}A+N^{\left(i\right)}R\ln \left[\frac{{U^{\left(i\right)}}^{\frac{3}{2}}{V}^{\left(i\right)}}{{N^{\left(i\right)}}^{\frac{5}{2}}}\right]-{N_1}^{\left(i\right)}R\ln \left[\frac{{N_1}^{\left(i\right)}}{N}\right]-{N_2}^{\left(i\right)}R\ln \left[\frac{{N_2}^{\left(i\right)}}{N}\right]\\ \\ N^{\left(i\right)}={N_1}^{\left(i\right)}+{N_2}^{\left(i\right)}\\ U^{\left(i\right)}={U_1}^{\left(i\right)}+{U_2}^{\left(i\right)}\end{array}\}i=1,2\Rightarrow \\ \end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}{S}^{\left(i\right)}=\left(N_1^{\left(i\right)}+N_2^{\left(i\right)}\right)A+N^{\left(i\right)}R\ln \left[\frac{{\left(U_1^{\left(i\right)}+U_2^{\left(i\right)}\right)}^{\frac{3}{2}}{V}^{\left(i\right)}}{{\left(N_1^{\left(i\right)}+N_2^{\left(i\right)}\right)}^{\frac{5}{2}}}\right]-N_1^{\left(i\right)}R\ln \left[\frac{N_1^{\left(i\right)}}{\left(N_1^{\left(i\right)}+N_2^{\left(i\right)}\right)}\right]-N_2^{\left(i\right)}R\ln \left[\frac{N_2^{\left(i\right)}}{\left(N_1^{\left(i\right)}+N_2^{\left(i\right)}\right)}\right]\\ i=1,2\\ \\ {\left(\frac{1}{T}\right)}^{\left(i\right)}={\left(\frac{\partial S^{\left(i\right)}}{\partial U^{\left(i\right)}}\right)}_{V,N_1^{\left(i\right)},N_2^{\left(i\right)}}\Rightarrow {\left(\frac{1}{T}\right)}^{\left(i\right)}=N^{\left(i\right)}R\frac{3}{2}\frac{1}{U^{\left(i\right)}}\\ \\ {\left(\frac{p}{T}\right)}^{\left(i\right)}={\left(\frac{\partial U^{\left(i\right)}}{\partial V^{\left(i\right)}}\right)}_{S,N_1^{\left(i\right)},N_2^{\left(i\right)}}\Rightarrow {\left(\frac{p}{T}\right)}^{\left(i\right)}=N^{\left(i\right)}R\frac{1}{V^{\left(i\right)}}\\ \\ {\left(\frac{{\mu }_1}{T}\right)}^{\left(i\right)}=-{\left(\frac{\partial U^{\left(i\right)}}{\partial N_1^{\left(i\right)}}\right)}_{S,V,N_2^{\left(i\right)}}\Rightarrow {\left(\frac{{\mu }_1}{T}\right)}^{\left(i\right)}=-A+\frac{5}{2}R-R\ln \left[\frac{{U^{\left(i\right)}}^{\frac{3}{2}}{V}^{\left(i\right)}}{{\left(N_1^{\left(i\right)}+N_2^{\left(i\right)}\right)}^{\frac{3}{2}}{N}_1^{\left(i\right)}}\right]\\ \\ {\left(\frac{{\mu }_2}{T}\right)}^{\left(i\right)}=-{\left(\frac{\partial U^{\left(i\right)}}{\partial N_2^{\left(i\right)}}\right)}_{S,V,N_1^{\left(i\right)}}\Rightarrow {\left(\frac{{\mu }_2}{T}\right)}^{\left(i\right)}=-A+\frac{5}{2}R-R\ln \left[\frac{U^{\frac{3}{2}}V}{{\left(N_1^{\left(i\right)}+N_2^{\left(i\right)}\right)}^{\frac{3}{2}}{N}_2^{\left(i\right)}}\right]\\ \end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}\begin{array}{c}d{S}^{\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}}=0\\ \\ d{S}^{\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}}=d{S}^{\left(1\right)}+d{S}^{\left(2\right)}\end{array}\}\Rightarrow d{S}^{\left(1\right)}+d{S}^{\left(2\right)}=0\end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}d{S}^{\left(1\right)}={\left(\frac{1}{T}\right)}^{\left(1\right)}d{U}^{\left(1\right)}+{\left(\frac{p}{T}\right)}^{\left(1\right)}d{V}^{\left(1\right)}-{\left(\frac{{\mu }_1}{T}\right)}^{\left(1\right)}d{N}_1^{\left(1\right)}-{\left(\frac{{\mu }_2}{T}\right)}^{\left(1\right)}d{N}_2^{\left(1\right)}\\ +\\ d{S}^{\left(2\right)}={\left(\frac{1}{T}\right)}^{\left(2\right)}d{U}^{\left(2\right)}+{\left(\frac{p}{T}\right)}^{\left(2\right)}d{V}^{\left(2\right)}-{\left(\frac{{\mu }_1}{T}\right)}^{\left(2\right)}d{N}_1^{\left(2\right)}-{\left(\frac{{\mu }_2}{T}\right)}^{\left(2\right)}d{N}_2^{\left(2\right)}\end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}d{S}^{\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}}=\left\{{\left(\frac{1}{T}\right)}^{\left(1\right)}-{\left(\frac{1}{T}\right)}^{\left(2\right)}\right\}d{U}^{\left(1\right)}+\left\{{\left(\frac{p}{T}\right)}^{\left(1\right)}-{\left(\frac{p}{T}\right)}^{\left(2\right)}\right\}d{V}^{\left(1\right)}-\\ \\ -\left\{{\left(\frac{{\mu }_1}{T}\right)}^{\left(1\right)}-{\left(\frac{{\mu }_1}{T}\right)}^{\left(2\right)}\right\}d{N}_1^{\left(1\right)}-\left\{{\left(\frac{{\mu }_2}{T}\right)}^{\left(1\right)}-{\left(\frac{{\mu }_2}{T}\right)}^{\left(2\right)}\right\}d{N}_2^{\left(1\right)}\\ \end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}{U}^{\left(1\right)}+U^{\left(2\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{U}^{\left(1\right)}+d{U}^{\left(2\right)}=0\Rightarrow d{U}^{\left(2\right)}=-d{U}^{\left(1\right)}\\ \\ V^{\left(1\right)}+V^{\left(2\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{V}^{\left(1\right)}+d{V}^{\left(2\right)}=0\Rightarrow d{V}^{\left(2\right)}=-d{V}^{\left(1\right)}\\ \\ N_1^{\left(1\right)}+N_1^{\left(2\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{N}_1^{\left(1\right)}+d{N}_1^{\left(2\right)}=0\Rightarrow d{N}_1^{\left(2\right)}=-d{N}_1^{\left(1\right)}\\ \\ N_2^{\left(1\right)}+N_2^{\left(2\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{N}_2^{\left(1\right)}+d{N}_2^{\left(2\right)}=0\Rightarrow d{N}_2^{\left(1\right)}=-d{N}_2^{\left(2\right)}\\ \\ \end{array}\end{array}$$

  $\left\{{\left(\frac{1}{T}\right)}^{\left(1\right)}-{\left(\frac{1}{T}\right)}^{\left(2\right)}\right\}=0\Rightarrow {\left(\frac{1}{T}\right)}^{\left(1\right)}={\left(\frac{1}{T}\right)}^{\left(2\right)}\Rightarrow N^{\left(1\right)}R\frac{3}{2}\frac{1}{U^{\left(1\right)}}=N^{\left(2\right)}R\frac{3}{2}\frac{1}{U^{\left(2\right)}}\Rightarrow \boxed{{\displaystyle \frac{N^{\left(1\right)}}{U^{\left(1\right)}}=\frac{N^{\left(2\right)}}{U^{\left(2\right)}}}}$

  $\left\{{\left(\frac{p}{T}\right)}^{\left(1\right)}-{\left(\frac{p}{T}\right)}^{\left(2\right)}\right\}=0\Rightarrow {\left(\frac{p}{T}\right)}^{\left(1\right)}={\left(\frac{p}{T}\right)}^{\left(2\right)}\Rightarrow N^{\left(1\right)}R\frac{1}{V^{\left(1\right)}}=N^{\left(2\right)}R\frac{1}{V^{\left(2\right)}}\Rightarrow \boxed{{\displaystyle \frac{N^{\left(1\right)}}{V^{\left(1\right)}}=\frac{N^{\left(2\right)}}{V^{\left(2\right)}}}}$

  $$\begin{array}{r}\begin{array}{l}\left\{{\left(\frac{{\mu }_1}{T}\right)}^{\left(1\right)}-{\left(\frac{{\mu }_1}{T}\right)}^{\left(2\right)}\right\}=0\Rightarrow {\left(\frac{{\mu }_1}{T}\right)}^{\left(1\right)}={\left(\frac{{\mu }_1}{T}\right)}^{\left(2\right)}\Rightarrow \\ \\ -A+\frac{5}{2}R-R\ln \left[\frac{{U^{\left(1\right)}}^{\frac{3}{2}}{V}^{\left(1\right)}}{{\left(N_1^{\left(1\right)}+N_2^{\left(1\right)}\right)}^{\frac{3}{2}}{N}_1^{\left(1\right)}}\right]=-A+\frac{5}{2}R-R\ln \left[\frac{{U^{\left(2\right)}}^{\frac{3}{2}}{V}^{\left(2\right)}}{{\left(N_1^{\left(2\right)}+N_2^{\left(2\right)}\right)}^{\frac{3}{2}}{N}_1^{\left(2\right)}}\right]\Rightarrow \\ \\ \frac{{U^{\left(1\right)}}^{\frac{3}{2}}{V}^{\left(1\right)}}{{\left(N_1^{\left(1\right)}+N_2^{\left(1\right)}\right)}^{\frac{3}{2}}{N}_1^{\left(1\right)}}=\frac{{U^{\left(2\right)}}^{\frac{3}{2}}{V}^{\left(2\right)}}{{\left(N_1^{\left(2\right)}+N_2^{\left(2\right)}\right)}^{\frac{3}{2}}{N}_1^{\left(2\right)}}\Rightarrow \boxed{{\displaystyle \frac{{U^{\left(1\right)}}^{\frac{3}{2}}{V}^{\left(1\right)}}{N_1^{\left(1\right)}}=\frac{{U^{\left(2\right)}}^{\frac{3}{2}}{V}^{\left(2\right)}}{N_1^{\left(2\right)}}}}\end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}\left\{{\left(\frac{{\mu }_2}{T}\right)}^{\left(1\right)}-{\left(\frac{{\mu }_2}{T}\right)}^{\left(2\right)}\right\}=0\Rightarrow {\left(\frac{{\mu }_2}{T}\right)}^{\left(1\right)}={\left(\frac{{\mu }_2}{T}\right)}^{\left(2\right)}\Rightarrow \\ \\ -A+\frac{5}{2}R-R\ln \left[\frac{{U^{\left(1\right)}}^{\frac{3}{2}}{V}^{\left(1\right)}}{{\left(N_1^{\left(1\right)}+N_2^{\left(1\right)}\right)}^{\frac{3}{2}}{N}_2^{\left(1\right)}}\right]=-A+\frac{5}{2}R-R\ln \left[\frac{{U^{\left(2\right)}}^{\frac{3}{2}}{V}^{\left(2\right)}}{{\left(N_1^{\left(2\right)}+N_2^{\left(2\right)}\right)}^{\frac{3}{2}}{N}_2^{\left(2\right)}}\right]\\ \\ \frac{{U^{\left(1\right)}}^{\frac{3}{2}}{V}^{\left(1\right)}}{{\left(N_1^{\left(1\right)}+N_2^{\left(1\right)}\right)}^{\frac{3}{2}}{N}_2^{\left(1\right)}}=\frac{{U^{\left(2\right)}}^{\frac{3}{2}}{V}^{\left(2\right)}}{{\left(N_1^{\left(2\right)}+N_2^{\left(2\right)}\right)}^{\frac{3}{2}}{N}_2^{\left(2\right)}}\Rightarrow \boxed{{\displaystyle \frac{{U^{\left(1\right)}}^{\frac{3}{2}}{V}^{\left(1\right)}}{N_2^{\left(1\right)}}=\frac{{U^{\left(2\right)}}^{\frac{3}{2}}{V}^{\left(2\right)}}{N_2^{\left(2\right)}}}}\\ \\ \end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}d{S}^{\left(1\right)}={\left(\frac{1}{T}\right)}^{\left(1\right)}d{U}^{\left(1\right)}+{\left(\frac{p}{T}\right)}^{\left(1\right)}d{V}^{\left(1\right)}-{\left(\frac{{\mu }_1}{T}\right)}^{\left(1\right)}d{N}_1^{\left(1\right)}-{\left(\frac{{\mu }_2}{T}\right)}^{\left(1\right)}d{N}_2^{\left(1\right)}\\ +\\ d{S}^{\left(2\right)}={\left(\frac{1}{T}\right)}^{\left(2\right)}d{U}^{\left(2\right)}+{\left(\frac{p}{T}\right)}^{\left(2\right)}d{V}^{\left(2\right)}-{\left(\frac{{\mu }_1}{T}\right)}^{\left(2\right)}d{N}_1^{\left(2\right)}-{\left(\frac{{\mu }_2}{T}\right)}^{\left(2\right)}d{N}_2^{\left(2\right)}\end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}d{S}^{\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}}=\left\{{\left(\frac{1}{T}\right)}^{\left(1\right)}-{\left(\frac{1}{T}\right)}^{\left(2\right)}\right\}d{U}^{\left(1\right)}+\left\{{\left(\frac{p}{T}\right)}^{\left(1\right)}-{\left(\frac{p}{T}\right)}^{\left(2\right)}\right\}d{V}^{\left(1\right)}-\\ \\ -\left\{{\left(\frac{{\mu }_1}{T}\right)}^{\left(1\right)}-{\left(\frac{{\mu }_1}{T}\right)}^{\left(2\right)}\right\}d{N}_1^{\left(1\right)}-\left\{{\left(\frac{{\mu }_2}{T}\right)}^{\left(1\right)}-{\left(\frac{{\mu }_2}{T}\right)}^{\left(2\right)}\right\}d{N}_2^{\left(1\right)}\\ \end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}{U}^{\left(1\right)}+U^{\left(2\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{U}^{\left(1\right)}+d{U}^{\left(2\right)}=0\Rightarrow d{U}^{\left(2\right)}=-d{U}^{\left(1\right)}\\ \\ {\left\{U^{\left(1\right)}+U^{\left(2\right)}\right\}}^{\left(i\right)}={\left\{\left(N_1^{\left(1\right)}+\frac{3}{4}\right)R\frac{3}{2}{T}^{\left(1\right)}+\left(N_1^{\left(2\right)}+\frac{1}{2}\right)R\frac{3}{2}{T}^{\left(2\right)}\right\}}^{\left(i\right)}\\ \\ \left\{U^{\left(1\right)}+U^{\left(2\right)}\right\}=\left\{\left(\frac{1}{2}+\frac{3}{4}\right)R\frac{3}{2}300+\left(1+\frac{1}{2}\right)R\frac{3}{2}250\right\}\Rightarrow U^{\left(1\right)}+U^{\left(2\right)}=R\frac{3}{2}\left(\frac{5}{4}300+\frac{3}{2}250\right)=1125R\\ \\ U^{\left(1\right)}+U^{\left(2\right)}=1125R\\ \\ V^{\left(1\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{V}^{\left(1\right)}=0\\ V^{\left(2\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{V}^{\left(2\right)}=0\\ V^{\left(1\right)}=V^{\left(2\right)}=V\\ \\ N_1^{\left(1\right)}+N_1^{\left(2\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{N}_1^{\left(1\right)}+d{N}_1^{\left(2\right)}=0\Rightarrow d{N}_1^{\left(2\right)}=-d{N}_1^{\left(1\right)}\\ \\ N_2^{\left(1\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{N}_2^{\left(1\right)}=0\\ N_2^{\left(2\right)}=\mathrm{K}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\Rightarrow d{N}_2^{\left(2\right)}=0\\ N_2^{\left(1\right)}=\frac{3}{4}\\ N_2^{\left(2\right)}=\frac{1}{2}\end{array}\end{array}$$
  $$\begin{array}{r}\begin{array}{l}\left\{{\left(\frac{1}{T}\right)}^{\left(1\right)}-{\left(\frac{1}{T}\right)}^{\left(2\right)}\right\}=0\Rightarrow {\left(\frac{1}{T}\right)}^{\left(1\right)}={\left(\frac{1}{T}\right)}^{\left(2\right)}\Rightarrow \frac{\left(N_1^{\left(1\right)}+\frac{3}{4}\right)}{U^{\left(1\right)}}=\frac{\left(N_1^{\left(2\right)}+\frac{1}{2}\right)}{U^{\left(2\right)}}\\ \\ \\ \left\{{\left(\frac{{\mu }_1}{T}\right)}^{\left(1\right)}-{\left(\frac{{\mu }_1}{T}\right)}^{\left(2\right)}\right\}=0\Rightarrow {\left(\frac{{\mu }_1}{T}\right)}^{\left(1\right)}={\left(\frac{{\mu }_1}{T}\right)}^{\left(2\right)}\Rightarrow \frac{{U^{\left(1\right)}}^{\frac{3}{2}}}{{\left(N_1^{\left(1\right)}+\frac{3}{4}\right)}^{\frac{3}{2}}{N}_1^{\left(1\right)}}=\frac{{U^{\left(2\right)}}^{\frac{3}{2}}}{{\left(N_1^{\left(2\right)}+\frac{1}{2}\right)}^{\frac{3}{2}}{N}_1^{\left(2\right)}}\\ \\ U^{\left(1\right)}+U^{\left(2\right)}=1125R\\ \\ N_1^{\left(1\right)}+N_1^{\left(2\right)}=\frac{3}{2}\end{array}\}\Rightarrow \end{array}$$
  $$\begin{array}{r}\boxed{{\displaystyle \begin{array}{l}{N}_1^{\left(1\right)}=N_1^{\left(2\right)}=\frac{3}{4}\\ \\ U^{\left(1\right)}=\frac{6}{5}{U}^{\left(2\right)}\Rightarrow U^{\left(2\right)}=\frac{5}{11}{U}^{\left(\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}\right)}\Rightarrow U^{\left(1\right)}=\frac{6}{11}{U}^{\left(\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}\right)}\\ \\ T=\frac{8}{33}\frac{1}{R}{U}^{\left(\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}\right)}\\ \\ {\left(\frac{p}{T}\right)}^{\left(1\right)}=\frac{4}{55}{U}^{\left(\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}\right)}\\ \\ {\left(\frac{p}{T}\right)}^{\left(2\right)}=\frac{2}{33}{U}^{\left(\mathrm{o}\mathrm{s}\mathrm{o}\mathrm{a}\right)}\end{array}}}\end{array}$$

---

Testuingurua

22. ARIKETA

He gasa duen gordailuak 1000 l-ko bolumenekoa da. Gasa 0.5 atm-n eta 20 ${}^{\circ }$C-ko tenperaturan dago. Bolumen berdineko bigarren gordailuan dagoen He gasa 1 atm-n eta 80 ${}^{\circ }$C-ko tenperaturan dago. Gordailu biak loturik dituen balbula ireki da. Demagun gasa monoatomikoa eta ideala dela, eta gordailuen hormak finkoak eta adiabatikoak.

Lortu sistemari dagozkion amaierako tenperatura eta presioa.

(C 3.4.4)

Emaitza

Ebazpen posible bat…

---

Testuingurua

23. ARIKETA

Bi sistemari dagozkion egoera-ekuazioak ondokoak dira:

$$\frac{1}{T^{(1)}}=\frac{3}{2}R\frac{N^{(1)}}{U^{(1)}}$$

$$\frac{1}{T^{(2)}}=\frac{5}{2}R\frac{N^{(2)}}{U^{(2)}}$$

Adierazpen horietan $R=1.986$ cal/mol K da balioko konstantea. Lehenengo sistemaren mol-kopurua $N^{(1)}=2$ da, eta bigarrenarena $N^{(2)}=3$. Sistema horiek diatermoa den bereizte-hormak banatu ditu. Sistema konposatuaren energia 6000 cal da.

Oreka lortutakoan, zenbatekoa da sistema bakoitzari dagokion barne-energia?

(C 2.6.3)

Emaitza

Ebazpen posible bat…

---

Testuingurua

24. ARIKETA

Aurreko ariketako azpisistemak, diatermoa den bereizte-hormaren bidez banatuta daude. Mol kopuruen balioak ondokoak dira: $N^{(1)}=2$ eta $N^{(2)}=3$. Hasierako tenperaturak $T^{(1)}=250$ K eta $T^{(2)}=350$ K dira.

Oreka lortutakoan,

1. Zein dira $U^{(1)}$ eta $U^{(2)}$ parametroen balioak?

2. Zein da oreka-tenperatura?

(C 2.6.4)

Emaitza

Ebazpen posible bat…

---

Testuingurua

25. ARIKETA

Bi sistemari dagozkion egoera-ekuazioak ondokoak dira:

1. ${\left(\frac{1}{T}\right)}^{(1)}=\frac{3}{2}R\frac{N^{(1)}}{U^{(1)}}$

2. ${\left(\frac{p}{T}\right)}^{(1)}=R\frac{N^{(1)}}{V^{(1)}}$

eta

1. ${\left(\frac{1}{T}\right)}^{(2)}=\frac{5}{2}R\frac{N^{(2)}}{U^{(2)}}$

2. ${\left(\frac{p}{T}\right)}^{(2)}=R\frac{N^{(2)}}{V^{(2)}}$

Adierazpen horietan $R=1.986$ cal/mol K da. $N^{(1)}=0.5$ eta $N^{(2)}=0.75$ dira. Sistema biak isolaturiko zilindroaren barnean daude, higikorra den pistoi isotermoak banandurik. Hasierako tenperaturak $T^{(1)}=200$ K eta $T^{(2)}=300$ K dira, eta bolumen osoa 20 l.

Oreka lortutakoan:

1. zein dira sistema bakoitzari dagozkion energia eta bolumena?

2. Zein dira presioa eta tenperatura?

(C 2.7.1)

Emaitza

Ebazpen posible bat…

ttttttt

---

Testuingurua

ARIKETA Gehigarriak

7.3-1. Thermodynamicists sometimes refer to the “first $TdS$ equation” and the “second $TdS$ equation”;

$$\begin{array}{r}\begin{array}{ll}TdS=N{c}_{v}dT+\left(T\alpha /{\kappa }_T\right)dV& (N\text{ constant })\\ TdS=N{c}_{P}dT-TV\alpha dP& (N\text{ constant })\end{array}\end{array}$$

Derive these equations.

---

7.3-2. Show that the second equation in the preceding problem leads directly to the relation

$$T{\left(\frac{\partial s}{\partial T}\right)}_v=c_P-Tv\alpha {\left(\frac{\partial P}{\partial T}\right)}_v$$

and so validates equation 7.36 .

---

Adiabatic Compression

Consider a single-component system of some definite quantity of matter (characterized by the mole number $N$ ) enclosed within an adiabatic wall. The initial temperature and pressure of the system are known. The system is compressed quasi-statically so that the pressure increases from its initial value $P$, to some definite final value $P_f$. We attempt to predict the changes in the various thermodynamic parameters (e.g., in the volume, temperature, internal energy, and chemical potential) of the system.

(C 7.2.1), (C 7.2.2), (C 7.4.1)

Emaitza

Ebazpen posible bat…

ttttttt

---

Kalkulu termodinamikoa eta zenbait aplikazio

---

Testuingurua

26. ARIKETA

Lortu ${\left(\frac{\partial T}{\partial v}\right)}_h$ koefizientearen adierazpena, ($C_p$, $\alpha$, ${\kappa }_T$) sortaren funtzioan.

(C 7.4.1)

---

Modu berean ere, lortu, kalkulu termodinamiko hutsa erabiliz, honako koefiziente hauek:

1. ${\left(\frac{\partial H}{\partial V}\right)}_{T,N}$

2. ${\left(\frac{\partial v}{\partial s}\right)}_p$

3. ${\left(\frac{\partial s}{\partial f}\right)}_v$

4. ${\left(\frac{\partial s}{\partial f}\right)}_p$

5. ${\left(\frac{\partial g}{\partial f}\right)}_p)$

6. ${\left(\frac{\partial s}{\partial v}\right)}_h$

7. (C 7.4.6): ${\left(\frac{\partial h}{\partial v}\right)}_u$

8. (C 7.4.17): ${\left(\frac{\partial \mu }{\partial v}\right)}_s$

Emaitza

${\left(\frac{\partial T}{\partial v}\right)}_h=-\frac{c_p-v\alpha p}{(c_v{\kappa }_T+v\alpha )}$

---

1. ${\left(\frac{\partial H}{\partial V}\right)}_{T,N}=\frac{1}{{\kappa }_T}(T\alpha -1)$

2. ${\left(\frac{\partial v}{\partial s}\right)}_p=Tv\frac{\alpha }{c_p}$

3. ${\left(\frac{\partial s}{\partial f}\right)}_v=-\frac{c_v}{T\cdot s}$

4. ${\left(\frac{\partial s}{\partial f}\right)}_p=-\frac{T}{c_p(s+pv\alpha )}$

5. ${\left(\frac{\partial g}{\partial f}\right)}_p=-\frac{1}{c_p}(s+pV\alpha )$

6. ${\left(\frac{\partial s}{\partial v}\right)}_h=\frac{c_p}{T}\frac{1}{(c_v{\kappa }_T+v\alpha )}$

7. (C 7.4.6):
   ${\left(\frac{\partial h}{\partial v}\right)}_u=[p-\frac{c_p-v\alpha p}{{\kappa }_T{c}_p-{\alpha }^{2}Tv}]$

8. (C 7.4.17):
   ${\left(\frac{\partial \mu }{\partial v}\right)}_s=\frac{1}{{\kappa }_T{\mathrm{c}}_v}(T\alpha s-c_p)$

Ebazpen posible bat…

$$\begin{array}{r}\begin{array}{l}{\left(\frac{\partial T}{\partial v}\right)}_h=-\frac{{\left(\frac{\partial h}{\partial v}\right)}_T}{{\left(\frac{\partial h}{\partial T}\right)}_v}\\ dh=Tds+vdp\\ {\left(\frac{\partial h}{\partial v}\right)}_T={\left(\frac{\partial (Tds+vdp)}{\partial v}\right)}_T=T{\left(\frac{\partial s}{\partial v}\right)}_T+v{\left(\frac{\partial p}{\partial v}\right)}_T=T{\left(\frac{\partial p}{\partial T}\right)}_v+v\frac{1}{{\left(\frac{\partial v}{\partial p}\right)}_T}=T\frac{\alpha }{{\kappa }_T}-\frac{1}{{\kappa }_T}=\frac{1}{{\kappa }_T}(T\alpha -1)\\ {\left(\frac{\partial h}{\partial T}\right)}_v={\left(\frac{\partial (Tds+vdp)}{\partial T}\right)}_v=T{\left(\frac{\partial s}{\partial T}\right)}_v+v{\left(\frac{\partial p}{\partial T}\right)}_v=c_V+v\frac{\alpha }{{\kappa }_T}\\ c_p-c_V=\frac{Tv{\alpha }^2}{{\kappa }_T}\\ {\left(\frac{\partial T}{\partial v}\right)}_h=-\frac{\frac{1}{{\kappa }_T}(T\alpha -1)}{T{c}_V+v\frac{d}{{\kappa }_T}}\end{array}\}\Rightarrow {\left(\frac{\partial T}{\partial v}\right)}_h=-\frac{(T\alpha -1)}{{\kappa }_T{}^{c_V}+v\alpha }\end{array}$$

---

Abiapuntuan, $h$ entalpia funtzioaren diferentzial osoa dago:

$$dh=Tds+vdp$$

Dagoeneko, adierazpen horretan badago diferentziala eginda, aldaketa osoa.

Kalkulatu beharreko ${\left(\frac{\partial h}{\partial v}\right)}_T$ koefizientea, beste modu honetan idatz daiteke, ondo interpretatatzeko:

$${\left({\displaystyle \frac{\partial [dh=Tds+vdp]}{\partial v}}\right)}_T\Rightarrow {\left(\frac{\partial h}{\partial v}\right)}_T={\left({\displaystyle \frac{\partial [Tds+vdp]}{\partial v}}\right)}_T$$

Azken adierazpen horretan, idatzi $s$ eta $p$, $v$ eta $T$ aldagaien funtzioan. Kontua da idatzitako adierazpenean, erabilitako aldagaiak $v$ eta $T$ direla.

Orduan:

$$s=s(v,T)\Rightarrow ds={\left({\displaystyle \frac{\partial s}{\partial v}}\right)}_{T}dv+{\left({\displaystyle \frac{\partial s}{\partial T}}\right)}_{v}dT$$

$$p=s(v,T)\Rightarrow dp={\left({\displaystyle \frac{\partial p}{\partial v}}\right)}_{T}dv+{\left({\displaystyle \frac{\partial p}{\partial T}}\right)}_{v}dT$$

Beraz, berridatz honako adierazpen hau:

$[dh=Tds+vdp]$

$$dh=T[{\left({\displaystyle \frac{\partial s}{\partial v}}\right)}_{T}dv+{\left({\displaystyle \frac{\partial s}{\partial T}}\right)}_{v}dT]+[{\left({\displaystyle \frac{\partial p}{\partial v}}\right)}_{T}dv+{\left({\displaystyle \frac{\partial p}{\partial T}}\right)}_{v}dT]$$

Orain, honako honek: ${\left({\displaystyle \frac{\partial (Tds+vdp)}{\partial v}}\right)}_T$, $v$-rekiko deribatu partziala baina ez duela aukeratzen.

$$dh=T{[{\left({\displaystyle \frac{\partial s}{\partial v}}\right)}_{T}dv+{\left({\displaystyle \frac{\partial s}{\partial T}}\right)}_{v}dT]}_T+{[{\left({\displaystyle \frac{\partial p}{\partial v}}\right)}_{T}dv+{\left({\displaystyle \frac{\partial p}{\partial T}}\right)}_{v}dT]}_T$$

Beraz, goiko adierazpenean, $dT{|}_T$ atalek ez dute ekarpenik egingo.

Hortaz, honako hau izango da azken adierazpena:

$${\left({\displaystyle \frac{\partial [dh=Tds+vdp]}{\partial v}}\right)}_T\Rightarrow {\left(\frac{\partial h}{\partial v}\right)}_T=T{[{\left({\displaystyle \frac{\partial s}{\partial v}}\right)}_{T}dv+0]}_T+{[{\left({\displaystyle \frac{\partial p}{\partial v}}\right)}_{T}dv+0]}_T$$

---

---

Testuingurua

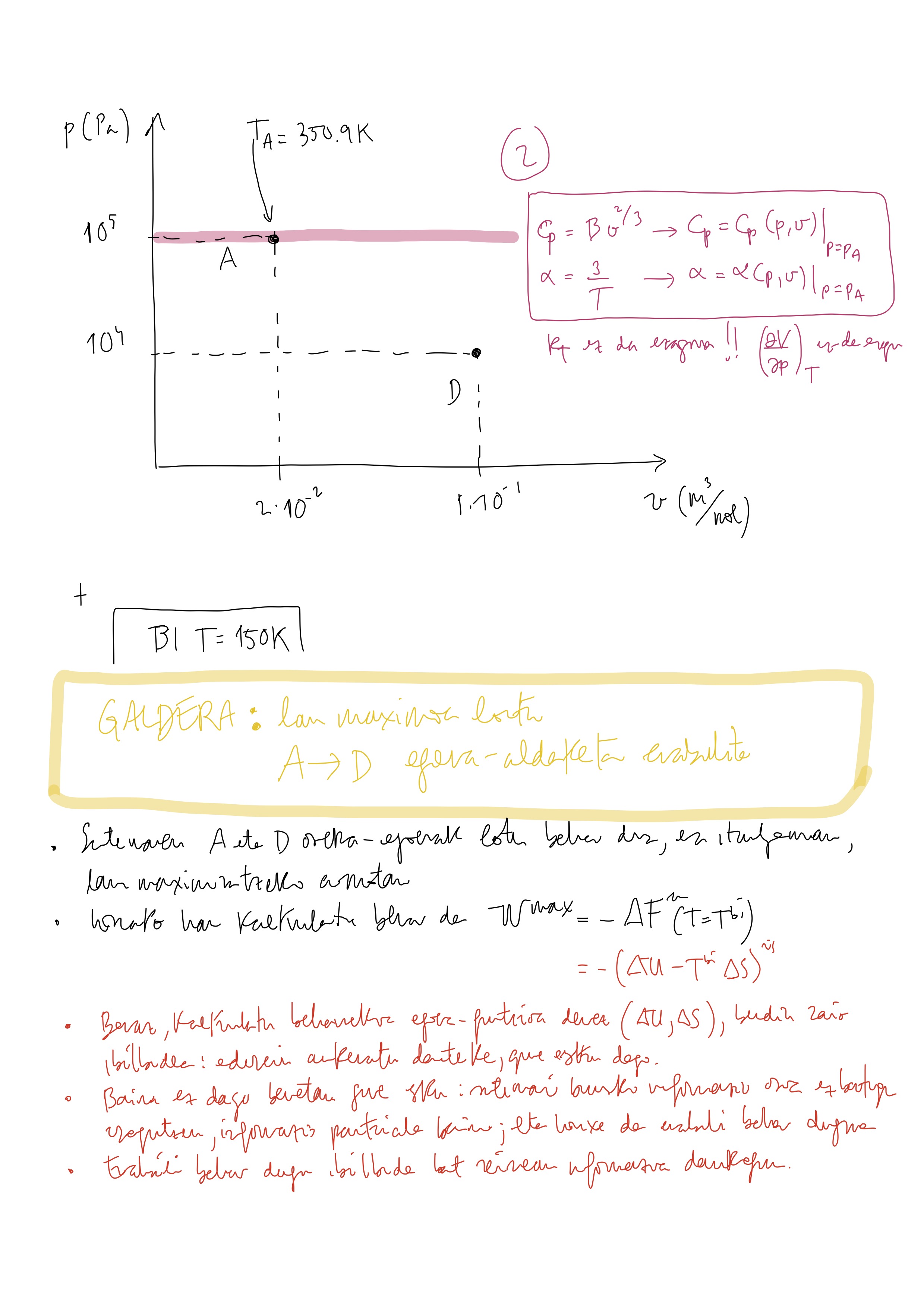
27. ARIKETA

Esku artean dugun gas errealaren bi molek 100 K-eko tenperaturan eta 2 MPa-eko presioan litro bateko gordailua bete dute. 10 cm${}^3$-ko balioko bolumenera era askean zabal dadila utzi diogu gasari. Lortu entalpia-aldaketa.

Hasierako egoerari dagozkion datuak honako hauek dira:

1. $c_p=0,8$ J/mol K,

2. ${\kappa }_T=3\times {10}^6$ Pa${}^{-1}$

3. $\alpha =0,002$ K${}^{-1}$

Emaitza

Ikus aurreko ariketako 7. ariketa.

Ebazpen posible bat…

$$\begin{array}{r}\begin{array}{l}dh=Tds+vdp\\ {\left(\frac{\partial h}{\partial v}\right)}_u={\left(\frac{\partial (Tds+vdp)}{\partial v}\right)}_u\Rightarrow {\left(\frac{\partial h}{\partial v}\right)}_u=T{\left(\frac{\partial s}{\partial v}\right)}_u+v{\left(\frac{\partial p}{\partial v}\right)}_u=-T\frac{{\left(\frac{\partial u}{\partial v}\right)}_s}{{\left(\frac{\partial u}{\partial s}\right)}_v}-v\frac{{\left(\frac{\partial u}{\partial v}\right)}_p}{{\left(\frac{\partial u}{\partial p}\right)}_v}\\ du=sdT-pdv\\ {\left(\frac{\partial u}{\partial v}\right)}_s={\left(\frac{\partial (Tds-pdv)}{\partial v}\right)}_s=T{\left(\frac{\partial s}{\partial v}\right)}_s-p{\left(\frac{\partial v}{\partial v}\right)}_s=-p\\ {\left(\frac{\partial u}{\partial s}\right)}_v={\left(\frac{\partial (Tds-pdv)}{\partial s}\right)}_v=T{\left(\frac{\partial s}{\partial s}\right)}_v-p{\left(\frac{\partial v}{\partial s}\right)}_v=T\\ {\left(\frac{\partial u}{\partial v}\right)}_p={\left(\frac{\partial (Tds-pdv)}{\partial v}\right)}_p=T{\left(\frac{\partial s}{\partial v}\right)}_p-p{\left(\frac{\partial v}{\partial v}\right)}_p=T{\left(\frac{\partial s}{\partial T}\right)}_p{\left(\frac{\partial T}{\partial v}\right)}_p-p=c_p\frac{1}{v\alpha }-p\\ {\left(\frac{\partial u}{\partial p}\right)}_v={\left(\frac{\partial (Tds-pdv)}{\partial p}\right)}_v=T{\left(\frac{\partial s}{\partial p}\right)}_v-p{\left(\frac{\partial v}{\partial p}\right)}_v=T{\left(\frac{\partial u}{\partial v}\right)}_s=p\\ {-v\frac{\partial u}{{\left(\frac{\partial u}{\partial v}\right)}_p}=-v\frac{c_p\frac{1}{v\alpha }-p}{c_V\frac{\partial T}{\alpha }})}_v=c_V\frac{{\kappa }_T}{\alpha }\\ {\left(\frac{\partial h}{\partial v}\right)}_u=p-v\frac{c_p\frac{1}{c_V-p}\frac{{\partial }_T}{\alpha }}{\partial p}\Rightarrow {\left(\frac{\partial h}{\partial v}\right)}_u=p-\frac{v\alpha (\frac{c_p}{v\alpha }-p)}{c_V{\kappa }_T}\end{array}\}\Rightarrow \end{array}$$

---

Testuingurua

28. ARIKETA

Frogatu ondoko berdintza beteko dela eta lortu horri dagokion adierazpena van der Waals-en gasaren kasurako:

$${\left(\frac{\partial c_v}{\partial v}\right)}_T=T{\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v$$

(C 7.4.7)

Emaitza

Idatzi $c_V$-ren, bolumen konstanteko bero-ahalamenaren, definizioa, entropiaren funtzioan.

Kontuan izan diferentzial zehatzek; hots, benetan existitzen diren funtzioek, bete beharreko baldintzetako bat, deribatu partzialekin lotutakoa bera.

Ebazpen posible bat…

$$\begin{array}{r}\begin{array}{c}{\left(\frac{\partial c_V}{\partial v}\right)}_T={\left(\frac{\partial \left\{T{\left(\frac{\partial s}{\partial T}\right)}_v\right\}}{\partial v}\right)}_T\Rightarrow {\left(\frac{\partial c_V}{\partial v}\right)}_T={\left(\frac{\partial T}{\partial v}\right)}_T{\left(\frac{\partial s}{\partial T}\right)}_v+T\left(\frac{{\partial }^{2}s}{\partial v\partial T}\right)\Rightarrow {\left(\frac{\partial c_V}{\partial v}\right)}_T=T\left(\frac{{\partial }^{2}s}{\partial T\partial v}\right)\Rightarrow \\ {\left(\frac{\partial c_V}{\partial v}\right)}_T=T{\left(\frac{\partial {\left(\frac{\partial s}{\partial v}\right)}_T}{\partial T}\right)}_v\Rightarrow {\left(\frac{\partial c_V}{\partial v}\right)}_T=T{\left(\frac{\partial {\left(\frac{\partial p}{\partial T}\right)}_v}{\partial T}\right)}_v\Rightarrow {\left(\frac{\partial c_V}{\partial v}\right)}_T=T{\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v\\ (p+\frac{a}{v^2})(v-b)=RT\Rightarrow p=\frac{RT}{(v-b)}-\frac{a}{v^2}\\ {\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v={\left(\frac{{\partial }^2(\frac{RT}{(v-b)}-\frac{a}{v^2})}{\partial T^2}\right)}_v\Rightarrow {\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v={\left(\frac{\partial \left(\frac{RT}{(v-b)}\right)}{\partial T}\right)}_v\Rightarrow {\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v=0\end{array}\end{array}$$

---

Testuingurua

29. ARIKETA

Frogatu ondoko berdintza beteko dela:

$${\left(\frac{\partial c_p}{\partial p}\right)}_T=-Tv\left[{\alpha }^2+{\left(\frac{\partial \alpha }{\partial T}\right)}_p\right]$$

Lortu berdintza horri dagokion adierazpena ondoko egoera-ekuazioa beteko duen sistemaren kasurako:

$$p(v+\frac{A}{T^2})=RT$$

(C 7.4.8)

Emaitza

Idatzi $c_p$-ren, bolumen konstanteko bero-ahalamenaren, definizioa, entropiaren funtzioan.

Kontuan izan diferentzial zehatzek; hots, benetan existitzen diren funtzioek, bete beharreko baldintzetako bat, deribatu partzialekin lotutakoa bera.

Ebazpen posible bat…

$$\begin{array}{r}\begin{array}{rl}& {\left(\frac{\partial c_p}{\partial p}\right)}_T={\left(\frac{\partial \left\{T{\left(\frac{\partial s}{\partial T}\right)}_p\right\}}{\partial p}\right)}_T\Rightarrow {\left(\frac{\partial c_p}{\partial p}\right)}_T={\left(\frac{\partial T}{\partial p}\right)}_T{\left(\frac{\partial s}{\partial T}\right)}_p+T\left(\frac{{\partial }^{2}s}{\partial p\partial T}\right)\Rightarrow {\left(\frac{\partial c_p}{\partial p}\right)}_T=T\left(\frac{{\partial }^{2}s}{\partial T\partial p}\right)\Rightarrow \\ & {\left(\frac{\partial c_p}{\partial p}\right)}_T=T{\left(\frac{\partial {\left(\frac{\partial s}{\partial p}\right)}_T}{\partial T}\right)}_p\Rightarrow {\left(\frac{\partial c_p}{\partial p}\right)}_T=T{\left(\frac{\partial {(-\frac{\partial v}{\partial T})}_p}{\partial T}\right)}_p\Rightarrow {\left(\frac{\partial c_p}{\partial p}\right)}_T=T{\left(\frac{\partial (-v\alpha {)}_p}{\partial T}\right)}_p\Rightarrow \\ & {\left(\frac{\partial c_p}{\partial p}\right)}_T=-T{({\left(\frac{\partial v}{\partial T}\right)}_p\alpha +v{\left(\frac{\partial \alpha }{\partial T}\right)}_p)}_p\Rightarrow {\left(\frac{\partial c_p}{\partial p}\right)}_T=-T{(v{\alpha }^2+v{\left(\frac{\partial \alpha }{\partial T}\right)}_p)}_p\Rightarrow \\ & {\left(\frac{\partial c_p}{\partial p}\right)}_T=-Tv{({\alpha }^2+{\left(\frac{\partial \alpha }{\partial T}\right)}_p)}_p\end{array}\end{array}$$

$$\begin{array}{r}\begin{array}{rl}& p(v+\frac{A}{T^2})=RT\Rightarrow v=\frac{RT}{p}-\frac{A}{T^2}\\ & \alpha =\frac{1}{v}{\left(\frac{\partial v}{\partial T}\right)}_p\Rightarrow \alpha =\frac{1}{(\frac{RT}{p}-\frac{A}{T^2})}{\left(\frac{\partial (\frac{RT}{p}-\frac{A}{T^2})}{\partial T}\right)}_p\Rightarrow \alpha =\frac{1}{(\frac{RT}{p}-\frac{A}{T^2})}(\frac{R}{p}+\frac{2A}{T^3})\\ & {\alpha }^2={\left(\frac{1}{(\frac{RT}{p}-\frac{A}{T^2})}(\frac{R}{p}+\frac{2A}{T^3})\right)}^2\\ & {\left(\frac{\partial \alpha }{\partial T}\right)}_p=\left(\frac{\partial \left(\frac{1}{(\frac{RT}{p}-\frac{A}{T^2})}(\frac{R}{p}+\frac{2A}{T^3})\right)}{\partial T}\right)\end{array}\end{array}$$

---

Testuingurua

30. ARIKETA

Aurreko ariketako mol bati $p_0$ hasierako presiotik $p_f$ bukaerako presiorainoko espantsio isotermoa eragin diogu.

Lortu prozesuan sistemak trukatu duen bero kantitatea.

(C 7.4.9)

Emaitza

$$Q=-\frac{2a}{T^2}\mathrm{\Delta }p+RT\ln \left(\frac{T^2{v}_0+a}{T^2{v}_f+a}\right)$$

Ebazpen posible bat…

• $\delta Q=TdS$, onartuz gertatu den prozesua itzulgarria dela (Prozesuaren adierazpena emanda dago, beraz, onartu daiteke) Kalkulatu behar da $S=S(T,p)$, aldagai independentetzat $T$ eta $p$ onartuz, lehenak konstante dirau eta bigarrenaren aldaketa ezaguna da.

  $${\left[\delta Q\right]}_T=T{(-\frac{\partial V}{\partial T})}_p{\left[dp\right]}_T\Rightarrow Q=-\frac{2a}{T^2}\mathrm{\Delta }p+RT\ln \left(\frac{p_0}{p_f}\right)$$

• Lehenengo Printzipioaren adierazpenetik abiatu daiteke ere bai:

• $$\delta Q=\underset{=-\frac{2a}{T^3}dp}{\underbrace{dU}}+\underset{=\frac{R{T}^3}{T^{2}V+a}dV}{\underbrace{pdV}}$$

---

Sistemari, presioa aldatuz, espantsioa eragin diogu; beraz, aldagai independentea $p$ presioa da. Beroaz galdatu dutenez, tenperatura konstanteko preozesuan, ondokoa adierazpena erabil dezakegu: $\delta Q=TdS$. Orduan, ondokoa da kalkulatu beharreko koefizientea: ${\left(\frac{\partial S}{\partial p}\right)}_T$

${\left(\frac{\partial S}{\partial p}\right)}_T=-{\left(\frac{\partial V}{\partial T}\right)}_p\Rightarrow {\left(\frac{\partial S}{\partial p}\right)}_T=-V\alpha$ $dS={\left(\frac{\partial S}{\partial p}\right)}_{T}dp\Rightarrow dS=(-V\alpha )dp\Rightarrow \int dS=\int (-V\alpha )dp$ ${\left(\frac{\partial S}{\partial p}\right)}_T=-{\left(\frac{\partial V}{\partial T}\right)}_p\Rightarrow {\left(\frac{\partial S}{\partial p}\right)}_T=-V\alpha$ $dS={\left(\frac{\partial S}{\partial p}\right)}_{T}dp\Rightarrow dS=(-V\alpha )dp\Rightarrow \int dS=\int (-V\alpha )dp$ $\begin{array}{l}\alpha =\frac{1}{(\frac{RT}{p}-\frac{A}{T^2})}(\frac{R}{p}+\frac{2A}{T^3})\\ v=\frac{RT}{p}-\frac{A}{T^2}\end{array}\}\Rightarrow -V\alpha =-(\frac{R}{p}+\frac{2A}{T^3})$ $\begin{array}{l}\mathrm{\Delta }S=\int -(\frac{R}{p}+\frac{2A}{T^3})dp\Rightarrow \mathrm{\Delta }S=-\{R\ln \frac{p_f}{p_i}+\frac{2A}{T^3}\mathrm{\Delta }p\}\\ Q=T\mathrm{\Delta }S\end{array}\}\Rightarrow Q=-T\{R\ln \frac{p_f}{p_i}+\frac{2A}{T^3}\mathrm{\Delta }p\}$

---

Testuingurua

31. ARIKETA

Esku artean dugun sistemaren kasuan ezagunak dira ondoko bi propietate hauek:

$$C_V=A{T}^3$$

$$(v-v_0)p=B(T)$$

Adierazpen horretan, $A$ konstantea da eta $B(T)$, tenperaturaren funtzio ezezaguna.

1. Eztabaidatu zer forma har dezakeen $B(T)$ funtzioak.

2. Lortu ($C_p$, $\alpha$, ${\kappa }_T$) sortakoak, $T$-ren eta $v$-ren funtzioan.

(C 7.4.22)

Emaitza

1. $B^{″}(T)=0\Rightarrow B(T)=DT+E\Rightarrow p=\frac{(DT+E)}{v-v_0}$

2. $c_p=A{T}^3+\frac{T^3}{(DT+E)}$

Adierazpen horietan $D$ eta $E$ konstanteak dira.

Ebazpen posible bat…

Aurreko ariketaren emaitza erabiliko dugu $B(T)$ funtzioaren forma finkatzeko. Beraz, jakina da ondoko adierazpena beteko dela: ${\left(\frac{\partial c_V}{\partial v}\right)}_T=T{\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v.$ Orduan, berdintzako atal biak, bakoitza bere aldetik, kalkulatu egingo dugu; eta, ondoren, alderatu.

$$\begin{array}{r}\begin{array}{rl}& {\left(\frac{\partial c_V}{\partial v}\right)}_T=T{\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v\\ & {\left(\frac{\partial c_V}{\partial v}\right)}_T={\left(\frac{\partial \left(A{T}^3\right)}{\partial v}\right)}_T\Rightarrow {\left(\frac{\partial c_V}{\partial v}\right)}_T=0\\ & (v-v_o)p=B(T)\Rightarrow p=\frac{B(T)}{(v-v_o)}\\ & {\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v={\left(\frac{{\partial }^2\left(\frac{B(T)}{(v-v_o)}\right)}{\partial T^2}\right)}_v=\frac{1}{(v-v_o)}{\left(\frac{{\partial }^2(B(T))}{\partial T^2}\right)}_v=\frac{1}{(v-v_o)}{B}^{\prime \prime }(T)\\ & T{\left(\frac{{\partial }^{2}p}{\partial T^2}\right)}_v=T\frac{1}{(v-v_o)}{B}^{\prime \prime }(T)\Rightarrow \\ & 0=T\frac{1}{(v-v_o)}{B}^{\prime \prime }(T)\Rightarrow 0=T{B}^{\prime \prime }(T)\Rightarrow B^{\prime \prime }(T)=0\Rightarrow B(T)=B_{1}T+B_2\end{array}\end{array}$$

(b) $(C_p,\alpha ,{\kappa }_T)$ sortakoak.

i. $\alpha$

$$\begin{array}{r}\begin{array}{l}p=\frac{B_{1}T+B_2}{(v-v_o)}\Rightarrow (v-v_o)=\frac{B_{1}T+B_2}{p}\\ \alpha =\frac{1}{v}{\left(\frac{\partial v}{\partial T}\right)}_p\Rightarrow \alpha =\frac{1}{(v-v_o)}{\left(\frac{\partial (v-v_o)}{\partial T}\right)}_p\Rightarrow \\ {\left(\frac{\partial (v-v_o)}{\partial T}\right)}_p={\left(\frac{\partial \left(\frac{B_{1}T+B_2}{p}\right)}{\partial T}\right)}_p=\frac{1}{p}{B}_1\end{array}\}\Rightarrow \alpha =\frac{1}{(v-v_o)}\frac{1}{p}{B}_1\end{array}$$

ii. ${\kappa }_T$

$$\begin{array}{r}\begin{array}{l}{\kappa }_T=-\frac{1}{v}{\left(\frac{\partial v}{\partial p}\right)}_T\Rightarrow {\kappa }_T=-\frac{1}{(v-v_o)}{\left(\frac{\partial (v-v_o)}{\partial p}\right)}_T\Rightarrow \\ {\left(\frac{\partial (v-v_o)}{\partial p}\right)}_T={\left(\frac{\partial \left(\frac{B_{1}T+B_2}{p}\right)}{\partial p}\right)}_T=-\frac{B_{1}T+B_2}{p^2}=-\frac{B_{1}T+B_2}{{\left(\frac{B_{1}T+B_2}{(v-v_o)}\right)}^2}=-\frac{{(v-v_o)}^2}{(B_{1}T+B_2)}=-\frac{(v-v_o)}{p}\\ {\kappa }_T=-\frac{1}{(v-v_o)}\{-\frac{(v-v_o)}{p}\}\Rightarrow {\kappa }_T=\frac{1}{p}\end{array}\}\Rightarrow \end{array}$$

iii. $C_p$

$$\begin{array}{r}\begin{array}{c}{c}_p-c_V=\frac{Tv{\alpha }^2}{{\kappa }_T}\Rightarrow c_p=c_V+\frac{Tv{\alpha }^2}{{\kappa }_T}\Rightarrow c_p=c_V+\frac{T(v-v_o){\alpha }^2}{{\kappa }_T}\\ \frac{T(v-v_o){\alpha }^2}{{\kappa }_T}=T(v-v_o)\frac{{\left(\frac{1}{(v-v_o)}\frac{1}{p}{B}_1\right)}^2}{\left(\frac{1}{p}\right)}=T\left(\frac{1}{(v-v_o)}\frac{1}{p}{B}_1^2\right)=T{B}_1^2(B_{1}T+B_2)\\ c_p=c_V+T{B}_1^2(B_{1}T+B_2)\\ {\left(\frac{\partial c_p}{\partial p}\right)}_T=-Tv\{{\alpha }^2+{\left(\frac{\partial \alpha }{\partial T}\right)}_p\}\Rightarrow {\left(\frac{\partial c_p}{\partial p}\right)}_T=-T(v-v_o)\{{\alpha }^2+{\left(\frac{\partial \alpha }{\partial T}\right)}_p\}\\ \alpha =\frac{1}{(v-v_o)}\frac{1}{p}{B}_1\Rightarrow {\alpha }^2={\left(\frac{1}{(v-v_o)}\frac{1}{p}{B}_1\right)}^2)\\ {\left(\frac{\partial \alpha }{\partial T}\right)}_p={\left(\frac{\partial \left(\frac{1}{(v-v_o)}\frac{1}{p}{B}_1\right)}{\partial T}\right)}_p=0\\ {\left(\frac{\partial c_p}{\partial p}\right)}_T=-T\frac{1}{(v-v_o)}{\left(\frac{1}{(B_{1}T+B_2)}{B}_1\right)}^2\end{array}\}\Rightarrow {\left(\frac{\partial c_p}{\partial p}\right)}_T=-T(v-v_o){\left(\frac{1}{(v-v_o)}\frac{1}{p}{B}_1\right)}^2\Rightarrow \end{array}$$

---

Testuingurua

32. ARIKETA

Van der Waalsen egoera-ekuazioa esleitu zaion 1 mol-eko sistemari $v_0$ hasierako bolumenetik $v_f$ bukaerako bolumenerako espantsio isotermoa eragin diogu.

Lortu prozesuan trukaturiko bero kantitatea.

(C 7.4.10)

Emaitza

${\left[\delta Q\right]}_T=T{\left(\frac{\partial p}{\partial T}\right)}_V{\left[dV\right]}_T$

$Q=3RT\ln \left(\frac{v_f-b}{v_i-b}\right)+\frac{2a}{v}$

Ebazpen posible bat…

$$\begin{array}{r}\begin{array}{rl}& {\left(\frac{\partial S}{\partial V}\right)}_T=-{\left(\frac{\partial p}{\partial T}\right)}_V=-\frac{{\left(\frac{\partial V}{\partial T}\right)}_p}{{\left(\frac{\partial V}{\partial p}\right)}_T}=\frac{\alpha }{{\kappa }_T}\\ & dS={\left(\frac{\partial S}{\partial V}\right)}_{T}dV\Rightarrow dS=\frac{\alpha }{{\kappa }_T}dV\Rightarrow \int dS=\int \frac{\alpha }{{\kappa }_T}dV\end{array}\end{array}$$

van der Waals-en fluidoaren kasuan, hobea da ${\left(\frac{\partial p}{\partial T}\right)}_V$ koefizientea kalkulatzea: egoera-ekuazioa hirugarren graduko polinomioa, bolumenean, baita. Orduan,

$$\begin{array}{r}\begin{array}{rl}& p=\frac{RT}{(v-b)}-\frac{a}{v^2}\\ & -{\left(\frac{\partial p}{\partial T}\right)}_V=-{\left(\frac{\partial (\frac{RT}{(v-b)}-\frac{a}{v^2})}{\partial T}\right)}_V\Rightarrow -{\left(\frac{\partial p}{\partial T}\right)}_V=-\frac{R}{(v-b)}\\ & dS=-{\left(\frac{\partial p}{\partial T}\right)}_{V}dV\Rightarrow dS=-\frac{R}{(v-b)}dV\Rightarrow \int dS=\int (-\frac{R}{(v-b)})dV\\ & \mathrm{\Delta }S=-R\ln \frac{(v_f-b)}{(v_i-b)}\}\Rightarrow \begin{array}{c}Q=-RT\ln \frac{(v_f-b)}{(v_i-b)}\\ Q=T\mathrm{\Delta }S\end{array}\end{array}\end{array}$$

---

Testuingurua

33. ARIKETA

Esku artean dugun oxigenoaren bi molak 0 ${}^{\circ }$C-ko tenperaturan eta 10${}^5$ Pa-eko presioan daude. Konpresio adiabatikoaren bidez bukaerako tenperatura 300 ${}^{\circ }$C-ko balioraino eraman da.

Lortu bukaerako presioaren balioa ondoko ekuazioa integratuz:

$$dT=\frac{Tv\alpha }{c_p}dp$$

Onartu ondoko bero-ahalmeneko gas ideala dela oxigenoa:

$$c_p=26.20+11.49\times {10}^{-3}T-3.223\times {10}^{-6}{T}^2$$

(C 7.4.11)

Emaitza

Ebazpen posible bat…

Lehenengo eta behin, kalkulatu dezagun ondoko koefizientea: $\left(\frac{\partial T}{\partial p}\right)$, aurreko adierazpenaren berdina dela konprobatzeko.

$$\begin{array}{r}\begin{array}{rl}& {\left(\frac{\partial T}{\partial p}\right)}_S=-\frac{{\left(\frac{\partial S}{\partial p}\right)}_T}{{\left(\frac{\partial S}{\partial T}\right)}_p}=-\frac{-{\left(\frac{\partial V}{\partial T}\right)}_p}{\frac{C_p}{T}}=\frac{T}{C_p}V\alpha \Rightarrow {\left(\frac{\partial T}{\partial p}\right)}_S=\frac{Tv\alpha }{c_p}\\ & dT={\left(\frac{\partial T}{\partial p}\right)}_{S}dp\Rightarrow dT=\frac{Tv\alpha }{c_p}dp\\ & c_p=a+bT+c{T}^2\\ & \mathrm{\Delta }p=\frac{1}{v\alpha }\int (\frac{a}{T}+b+cT)dT\Rightarrow \mathrm{\Delta }p=\frac{c_{p}dT}{T}=v\alpha dp\Rightarrow \frac{(a+bT+c{T}^2)dT}{v}=v\alpha dp\\ & p_f=p_i+\frac{1}{v\alpha }\{a\ln \frac{T_f}{T_i}+b(T_f-T_i)+\frac{1}{2}c(T_f^2-T_i^2)\}\end{array}\end{array}$$

---

Testuingurua

34. ARIKETA

Erraztu honako adierazpen hau:

$${\left(\frac{\partial u}{\partial p}\right)}_h$$

(C 7.4.13)

Emaitza

Nahiz eta liburuko (7.4.13 ariketa) enuntziatua honako hau den: Kalkulatu zenbatekoa den barne-energia molarraren aldaketa estrangulazio-prozezu batean, ($h$ konstantekoa bera) zeinean presio-aldaketa $dp$ izan den.

${\left(\frac{\partial u}{\partial p}\right)}_h=-v+p\frac{v\alpha }{c_p}(c_v\frac{{\kappa }_T}{\alpha }+v)$

Ebazpen posible bat…

---

Testuingurua

35. ARIKETA

Zabaltze askearen ondorioz esku artean dugun gasaren tenperatura-aldaketa $dT$ da.

Lortu presio-aldaketa.

(C 7.4.14)

Emaitza

Ebazpen posible bat…

Sistemari, bolumena aldatuz, zabaltze askea eragin diogu; beraz, aldagai independentea $V$ bolumena da.

Zabaltze askea denez, $U$ konstanteko prozesua da; eta presioaz galdetu dute, baina tenperatura-aldaketa ezagututa; orduan, honako hau da kalkulatu beharreko koefizientea:

$${\left(\frac{\partial p}{\partial T}\right)}_u$$

$$\begin{array}{r}\begin{array}{rl}& du=Tds-pdv\\ & {\left(\frac{\partial p}{\partial T}\right)}_u=-\frac{{\left(\frac{\partial u}{\partial T}\right)}_p}{{\left(\frac{\partial u}{\partial p}\right)}_T}=-\frac{{\left(\frac{\partial (Tds-pdv)}{\partial T}\right)}_p}{{\left(\frac{\partial (Tds-pdv)}{\partial p}\right)}_T}=-\frac{T{\left(\frac{\partial s}{\partial T}\right)}_p-p{\left(\frac{\partial v}{\partial T}\right)}_p}{T{\left(\frac{\partial s}{\partial p}\right)}_T-p{\left(\frac{\partial v}{\partial p}\right)}_T}=-\frac{c_p-pv\alpha }{-T{\left(\frac{\partial v}{\partial T}\right)}_p-p{\left(\frac{\partial v}{\partial p}\right)}_T}=-\frac{c_p-pv\alpha }{-Tv\alpha +pv{\kappa }_T}\\ & dp={\left(\frac{\partial p}{\partial T}\right)}_{u}dT\Rightarrow dp=\{-\frac{c_p-pv\alpha }{-Tv\alpha +pv{\kappa }_T}\}dT\end{array}\end{array}$$

---

Testuingurua

36. ARIKETA

Esku artean van der Waals-en fluidoaren 1 mol dugu: $T_i$ tenperaturan, eta $V_i$ bolumena betez. Balbula bat irekiz gasa dagoen gordailua hasieran hutsik zegoen beste gordailu batekin konektatu dugu, gasa $V_f$ bolumen osora hedatuz. Gordailuen hormak adiabatikoak dira. Lortu $T_f$ bukaerako tenperatura.

(C 7.4.15)

Emaitza

${\left(\frac{\partial T}{\partial V}\right)}_U=-\frac{T{\left(\frac{\partial S}{\partial V}\right)}_T-p}{C_V}\Rightarrow {\left[dT\right]}_U=-\frac{1}{C_V}\frac{a}{V^2}{\left[dV\right]}_U$

Ebazpen posible bat…

Sistemari, bolumena aldatuz, zabaltza askea eragin diogu; beraz, aldagai independentea $v$ bolumena da.

Zabaltze askea denez, $U$ konstanteko prozesua da; eta tenperaturaz galdetu dute; orduan, ondokoa da kalkulatu beharreko koefizientea:

$${\left(\frac{\partial T}{\partial v}\right)}_u$$

$$\begin{array}{r}\begin{array}{rl}& du=Tds-pdv\\ & {\left(\frac{\partial T}{\partial v}\right)}_u=-\frac{{\left(\frac{\partial u}{\partial v}\right)}_T}{{\left(\frac{\partial u}{\partial T}\right)}_v}=-\frac{{\left(\frac{\partial (Tds-pdv)}{\partial v}\right)}_T}{{\left(\frac{\partial (Tds-pdv)}{\partial T}\right)}_v}=-\frac{T{\left(\frac{\partial s}{\partial v}\right)}_T-p{\left(\frac{\partial v}{\partial v}\right)}_T}{T{\left(\frac{\partial s}{\partial T}\right)}_v-p{\left(\frac{\partial v}{\partial T}\right)}_v}=-\frac{T{\left(\frac{\partial p}{\partial T}\right)}_v-p}{T{\left(\frac{\partial s}{\partial T}\right)}_v}=-\frac{1}{c_V}(T\frac{\alpha }{{\kappa }_T}-p)\\ & dT={\left(\frac{\partial T}{\partial v}\right)}_{u}dv\Rightarrow dT=\{-\frac{1}{c_V}(T\frac{\alpha }{{\kappa }_T}-p)\}dv\end{array}\end{array}$$

$$\begin{array}{r}\begin{array}{rl}& (p+\frac{a}{v^2})(v-b)=RT\Rightarrow p=\frac{RT}{(v-b)}-\frac{a}{v^2}\\ & \end{array}\end{array}$$

$$\begin{array}{r}\begin{array}{l}(p+\frac{a}{v^2})(v-b)=RT\Rightarrow p=\frac{RT}{(v-b)}-\frac{a}{v^2}\\ \\ \begin{array}{c}\alpha =\frac{1}{v}{\left(\frac{\partial v}{\partial T}\right)}_p=-\frac{1}{v}\frac{{\left(\frac{\partial p}{\partial T}\right)}_v}{{\left(\frac{\partial p}{\partial v}\right)}_T}\\ {\kappa }_T=-\frac{1}{v}{\left(\frac{\partial v}{\partial p}\right)}_T=-\frac{1}{v}\frac{1}{{\left(\frac{\partial p}{\partial v}\right)}_T}\end{array}\}\Rightarrow \frac{\alpha }{{\kappa }_T}=\frac{(-\frac{1}{v}\frac{{\left(\frac{\partial p}{\partial T}\right)}_v}{{\left(\frac{\partial p}{\partial v}\right)}_T})}{(-\frac{1}{v}\frac{1}{{\left(\frac{\partial p}{\partial v}\right)}_T})}\Rightarrow \frac{\alpha }{{\kappa }_T}={\left(\frac{\partial p}{\partial T}\right)}_v\end{array}\}\Rightarrow \frac{\alpha }{{\kappa }_T}=\frac{R}{(v-b)}\Rightarrow \end{array}$$

$$dT=\{-\frac{1}{c_V}(T\frac{R}{(v-b)}-p)\}dv\Rightarrow dT=\{-\frac{1}{c_V}\frac{a}{v^2}\}dv\Rightarrow \int dT=\int \{-\frac{1}{c_V}\frac{a}{v^2}\}dv\Rightarrow$$

$$\mathrm{\Delta }T=\frac{a}{c_V}(\frac{1}{v_f}-\frac{1}{v_i})\Rightarrow \boxed{{\displaystyle T_f=T_i+\frac{a}{c_V}(\frac{1}{v_f}-\frac{1}{v_i})}}$$

---

Testuingurua

37. ARIKETA

Ebatz ezazu aurreko ariketa berbera; baina, kasu honetan, espantsioa adiabatikoa izateaz gain kuasiestatikoa dela onartuz.

(C 7.4.16)

Emaitza

Ebazpen posible bat…

$$\begin{array}{r}\begin{array}{rl}& {\left(\frac{\partial T}{\partial v}\right)}_s=-\frac{{\left(\frac{\partial s}{\partial v}\right)}_T}{{\left(\frac{\partial s}{\partial T}\right)}_v}==-\frac{{\left(\frac{\partial p}{\partial T}\right)}_v}{\frac{T}{T}{\left(\frac{\partial s}{\partial T}\right)}_v}=-\frac{1}{\frac{c_V}{T}}\frac{\alpha }{{\kappa }_T}=-\frac{T}{c_V}\frac{\alpha }{{\kappa }_T}\\ & dT={\left(\frac{\partial T}{\partial v}\right)}_{s}dv\Rightarrow dT=\{-\frac{T}{c_V}\frac{\alpha }{{\kappa }_T}\}dv\\ & (p+\frac{a}{v^2})(v-b)=RT\Rightarrow p=\frac{RT}{(v-b)}-\frac{a}{v^2}\end{array}\end{array}$$

$$\begin{array}{r}\begin{array}{l}(p+\frac{a}{v^2})(v-b)=RT\Rightarrow p=\frac{RT}{(v-b)}-\frac{a}{v^2}\\ \\ \begin{array}{c}\alpha =\frac{1}{v}{\left(\frac{\partial v}{\partial T}\right)}_p=-\frac{1}{v}\frac{{\left(\frac{\partial p}{\partial T}\right)}_v}{{\left(\frac{\partial p}{\partial v}\right)}_T}\\ {\kappa }_T=-\frac{1}{v}{\left(\frac{\partial v}{\partial p}\right)}_T=-\frac{1}{v}\frac{1}{{\left(\frac{\partial p}{\partial v}\right)}_T}\end{array}\}\Rightarrow \frac{\alpha }{{\kappa }_T}=\frac{(-\frac{1}{v}\frac{{\left(\frac{\partial p}{\partial T}\right)}_v}{{\left(\frac{\partial p}{\partial v}\right)}_T})}{(-\frac{1}{v}\frac{1}{{\left(\frac{\partial p}{\partial v}\right)}_T})}\Rightarrow \frac{\alpha }{{\kappa }_T}={\left(\frac{\partial p}{\partial T}\right)}_v\end{array}\}\Rightarrow \frac{\alpha }{{\kappa }_T}=\frac{R}{(v-b)}\Rightarrow \end{array}$$

$$\begin{array}{r}\begin{array}{rl}& dT={\left(\frac{\partial T}{\partial v}\right)}_{s}dv\Rightarrow dT=\{-\frac{T}{c_V}\frac{\alpha }{{\kappa }_T}\}dv\Rightarrow dT=-\frac{TR}{c_V(v-b)}dv\Rightarrow \frac{dT}{T}=-\frac{R}{c_V(v-b)}dv\Rightarrow \\ & \ln \frac{T_f}{T_i}=-\frac{R}{c_V}\ln \frac{(v_f-b)}{(v_i-b)}\Rightarrow \boxed{{\displaystyle T_f=T_i{\left[\frac{(v_f-b)}{(v_i-b)}\right]}^{-\frac{R}{c_V}}}}\end{array}\end{array}$$

---

Testuingurua

38. ARIKETA

Bolumenaren $\mathrm{\%}1$-eko beheratze adiabatikoak aldaketa jakina eragin du $\mu$ potentzial kimikoaren gainean. Zein bolumen-portzentajek izango du eragin berbera beheratze isotermoa bada?

(C 7.4.17)

Emaitza

Ebazpen posible bat…

Ondoko bi koefiziente hauek kalkulatu eta alderatu behar ditugu: ${\left(\frac{\partial \mu }{\partial v}\right)}_s$ eta ${\left(\frac{\partial \mu }{\partial v}\right)}_T$.

$$d\mu =-sdT+vdp$$

${\left(\frac{\partial \mu }{\partial v}\right)}_T={\left(\frac{\partial (-sdT+vdp)}{\partial v}\right)}_T=-s{\left(\frac{\partial T}{\partial v}\right)}_T+v{\left(\frac{\partial p}{\partial v}\right)}_T=v{\left(\frac{\partial p}{\partial v}\right)}_T=v\frac{1}{{\left(\frac{\partial v}{\partial p}\right)}_T}=-\frac{1}{{\kappa }_T}$

${\left(\frac{\partial \mu }{\partial v}\right)}_s=s\frac{{\left(\frac{\partial p}{\partial T}\right)}_v}{\frac{c_V}{T}}-v\frac{{\left(\frac{\partial s}{\partial T}\right)}_p{\left(\frac{\partial T}{\partial v}\right)}_p}{{\left(\frac{\partial s}{\partial T}\right)}_v{\left(\frac{\partial T}{\partial p}\right)}_v}=s\frac{T}{c_V}\frac{\alpha }{{\kappa }_T}-v\frac{c_p\frac{1}{{\left(\frac{\partial v}{\partial T}\right)}_p}}{c_V(-\frac{{\left(\frac{\partial v}{\partial p}\right)}_T}{{\left(\frac{\partial v}{\partial T}\right)}_p})}=s\frac{T}{c_V}\frac{\alpha }{{\kappa }_T}-\frac{c_p}{c_V{\kappa }_T}=-\frac{1}{c_V{\kappa }_T}(T\alpha s-c_p)$

${\left(\frac{\partial \mu }{\partial v}\right)}_T={\left(\frac{\partial (-sdT+vdp)}{\partial v}\right)}_T=-s{\left(\frac{\partial T}{\partial v}\right)}_T+v{\left(\frac{\partial p}{\partial v}\right)}_T=v{\left(\frac{\partial p}{\partial v}\right)}_T=v\frac{1}{{\left(\frac{\partial v}{\partial p}\right)}_T}=-\frac{1}{{\kappa }_T}$

$$\begin{array}{r}\begin{array}{l}{\left(\frac{\partial \mu }{\partial v}\right)}_s=-\frac{1}{{\kappa }_T}\left\{\frac{1}{c_V}(T\alpha s-c_p)\right\}\Rightarrow {\left(\frac{\partial \mu }{\partial v}\right)}_s={\left(\frac{\partial \mu }{\partial v}\right)}_T\left\{\frac{1}{c_V}(T\alpha s-c_p)\right\}\\ \\ \begin{array}{c}d\mu ={\left(\frac{\partial \mu }{\partial v}\right)}_{s}dv\\ d\mu ={\left(\frac{\partial \mu }{\partial v}\right)}_{T}dv\end{array}\}\Rightarrow (d\mu {)}_s=(d\mu {)}_T\Rightarrow {\left(\frac{\partial \mu }{\partial v}\right)}_s={\left(\frac{\partial \mu }{\partial v}\right)}_T\frac{dv}{v_o}100\Rightarrow \frac{dv}{v_o}100=\frac{{\left(\frac{\partial \mu }{\partial v}\right)}_s}{{\left(\frac{\partial \mu }{\partial v}\right)}_T}\end{array}\}\end{array}$$

$$\boxed{{\displaystyle \frac{dv}{v_o}100=\left\{\frac{1}{c_V}(T\alpha s-c_p)\right\}}}$$

---

Testuingurua

39. ARIKETA

Helio gasa erabiliz beteriko zilindroa pistoi batek itxi du. Zilindroaren aldeko horma adiabatikoa, higiezina eta helioarekiko iragaztezina da. Zilindroaren beheko aldea, berriz, isotermoa, higiezina eta helioarekiko iragazkorra da. Horma horren bidez, zilindroa $T$ tenperaturako bero-iturriarekin eta ${\mu }_{He}$ potentzial kimikoko materia-iturriarekin ukipenean dago.

1. Lortu sistemaren ($-\frac{1}{V}\frac{dV}{dp}$) konprimigarritasuna.

2. Frogatu konprimigarritasunak dibergentzia izango duela.

3. Zein da dibergentzia horren jatorri fisikoa?

(C 7.4.18)

Emaitza

Ebazpen posible bat…

Baldintza esperimentalen arabera, sistemaren tenperatura eta sisteman dagoen helioaren potentzial kimikoaren balioak finkoak dira: bero-iturri batekin eta materia-iturri batekin kontaktuan baitago sistema. Beraz, ondorioz, enuntziatuan aipaturiko $-\frac{1}{V}\frac{dV}{dp}$ konpresibilitatea tenperatura konstantekoa eta ${\mu }_{\text{He}}$ potentzial kimiko konstantekoa da; hots, ondoko hau: $-\frac{1}{V}\frac{dV}{dp}\to -\frac{1}{V}{\left(\frac{\partial V}{\partial p}\right)}_{T,{\mu }_{\mathrm{H}\mathrm{e}}}$.

Kasu honetan, edozer kalkulatzeko, potentzial termodinamikorik erabilgarriena ondoko hau da:

$$U[T,{\mu }_{\text{He}}]=U[T,{\mu }_{\text{He}}](T,V,{\mu }_{\text{He}})$$

hots, aldagai independenteen sorta naturala $\{T,V,{\mu }_{\text{He}}\}$ duena. Orduan, Legendreren bi transformazio burutu behar dugu $U$ barne-energiaren adierazpenetik $U[T,{\mu }_{\text{He}}]$ potentzial termodinamikoa lortzeko: $S$-ren ordez $T$ tenperatura ordezkatuko duena, lehenik; eta, ondoren, $N_{\text{He}}$-ren ordez ${\mu }_{\mathrm{H}\mathrm{e}}$ ordezkatuko duena.

Jakina, abiapuntua $U$ izan beharrean $F$ bada, Legendreren transformazio bakarra burutu behar da, $N_{\text{He}}\to {\mu }_{\mathrm{H}\mathrm{e}}$; baina, horrez gain, aldagai-aldaketa bat egin behar da:

$$F=F(T,V,N)\to F=F(T,V,N(T,V,{\mu }_{\text{He}}))$$

Abiatu gaitezen $F$ potentzial termodinamikotik; ondokoa da adierazpena:

$$F=-N_{\mathrm{H}\mathrm{e}}RT\ln \left[\frac{T^{\frac{3}{2}}V}{N_{\mathrm{H}\mathrm{e}}}\right]$$

Lortu dezagun:

$$F[{\mu }_{\text{He}}](=U[T,{\mu }_{\text{He}}])$$

Horretarako, ${\mu }_{\text{He}}$ lortuko dugu.

$${\mu }_{\mathrm{He}}\equiv {\left(\frac{\partial F}{\partial N_{\mathrm{He}}}\right)}_{T,V}\Rightarrow {\mu }_{\mathrm{He}}={\left(\frac{\partial (-N_{\mathrm{He}}RT\ln \left[\frac{T^{3}V}{N_{\mathrm{He}}}\right])}{\partial N_{\mathrm{He}}}\right)}_{T,V}\Rightarrow {\mu }_{\mathrm{He}}=-RT\ln \left[\frac{T^{3}V}{N_{\mathrm{He}}}\right]+RT$$

${\mu }_{\mathrm{He}}=RT[1-\ln \left[\frac{T^{3}V}{N_{\mathrm{He}}}\right]]$

$\frac{{\mu }_{\mathrm{He}}}{RT}=1-\ln \left[\frac{T^{\frac{3}{2}}V}{N_{\mathrm{He}}}\right]\Rightarrow \ln \left[\frac{T^{\frac{3}{2}}V}{N_{\mathrm{He}}}\right]=1-\frac{{\mu }_{\mathrm{He}}}{RT}\Rightarrow \frac{T^{\frac{3}{2}}V}{N_{\mathrm{He}}}=e^{(1-\frac{{\mu }_{\mathrm{He}}}{RT})}\Rightarrow N_{\mathrm{He}}=\frac{T^{\frac{3}{2}}V}{e^{(1-\frac{{\mu }_{\mathrm{He}}}{RT})}}$

$F\left[{\mu }_{\mathrm{He}}\right]=F-N_{\mathrm{He}}{\mu }_{\mathrm{He}}\Rightarrow F\left[{\mu }_{\mathrm{He}}\right]=F(T,V,{\mu }_{\mathrm{He}})-N_{\mathrm{He}}(T,V,{\mu }_{\mathrm{He}}){\mu }_{\mathrm{He}}$

$F\left[{\mu }_{\mathrm{He}}\right]=\{-\left(\frac{T^{\frac{3}{2}}V}{e^{(1-\frac{{\mu }_{\mathrm{He}}}{RT})}}\right)RT\ln \left[\frac{T^{\frac{3}{2}}V}{\left(\frac{T^{\frac{3}{2}}V}{e^{(1-\frac{{\mu }_{\mathrm{He}}}{RT})}}\right)}\right]\}-\left\{\frac{T^{\frac{3}{2}}V}{e^{(1-\frac{{\mu }_{\mathrm{HE}}}{RT})}}{\mu }_{\mathrm{He}}\right\}\Rightarrow$

$F\left[{\mu }_{\mathrm{He}}\right]=\{-\left(\frac{T^{\frac{3}{2}}V}{e^{(1-\frac{{\mu }_{\mathrm{He}}}{RT})}}\right)RT\ln \left[e^{(1-\frac{{\mu }_{\mathrm{He}}}{RT})}\right]\}-\left\{\frac{T^{\frac{3}{2}}V}{e^{(1-\frac{{\mu }_{\mathrm{HE}}}{RT})}}{\mu }_{\mathrm{He}}\right\}\Rightarrow$

$F\left[{\mu }_{\mathrm{He}}\right]=\{-\left(\frac{T^{\frac{3}{2}}V}{e^{(1-\frac{{\mu }_{\mathrm{He}}}{RT})}}\right)RT(1-\frac{{\mu }_{\mathrm{He}}}{RT})\}-\left\{T^{\frac{3}{2}}V{\mu }_{\mathrm{He}}{e}^{-(1-\frac{{\mu }_{\mathrm{He}}}{RT})}\right\}\Rightarrow$

$F\left[{\mu }_{\mathrm{He}}\right]=-R{T}^{\frac{5}{2}}V{e}^{-(1-\frac{{\mu }_{\mathrm{He}}}{RT})}$

$p\equiv -{\left(\frac{\partial F\left[{\mu }_{\mathrm{He}}\right]}{\partial V}\right)}_{T,{\mu }_{\mathrm{He}}}\Rightarrow p=-{\left(\frac{\partial (-R{T}^{\frac{5}{2}}V{e}^{-(1-\frac{{\mu }_{\mathrm{He}}}{RT})})}{\partial V}\right)}_{T,{\mu }_{\mathrm{He}}}\Rightarrow p=R{T}^{\frac{5}{2}}{e}^{-(1-\frac{{\mu }_{\mathrm{He}}}{RT})}$

---

Badago beste modu bat ariketa ebazteko, hainbesteko kalkulu egin gabe:

$${\left(\frac{\partial V}{\partial p}\right)}_{T,{\mu }_{\mathrm{He}}}=-\frac{{\left(\frac{\partial {\mu }_{\mathrm{He}}}{\partial p}\right)}_{T,V}}{{\left(\frac{\partial {\mu }_{\mathrm{He}}}{\partial V}\right)}_{T,p}}=\frac{v}{0}=\mathrm{\infty }$$

${\left(\frac{\partial {\mu }_{\mathrm{He}}}{\partial p}\right)}_{T,V}=v$ eta ${\left(\frac{\partial {\mu }_{\mathrm{He}}}{\partial V}\right)}_{T,p}=0$ definizioak baino ez dira.

He eta Ne gasen arteko nahastura dugunean, sistema konposatuak konpresibilitatea izango du: Ne-ak ezin baitu zilindrotik atera. Oraingo honetan, kalkulatu beharreko potentzial termodinamikoa ondoko hau da: $$F[{\mu }_{\text{He}}]=F(T,V,{\mu }_{\text{He}},N_{\text{Ne}})(=U[T,{\mu }_{\text{He}},N_{\text{Ne}}])$$

Jakina, sistema koposatuari, nahasturari, dagokion $F[\mu ]$ potentzial termodinamiko, azpisistema bakoitzari dagokionaren batura da: $F=F_{\text{He}}+F_{\text{Ne}}$. Orduan, $F$-ren aurreko adierazpenetik abiatuz, ondokoa izango dugu:

$F=F_{\mathrm{He}}+F_{\mathrm{Ne}}$

$F=-N_{\mathrm{He}}RT\ln \left[\frac{T^{3}V}{N_{\mathrm{He}}}\right]-N_{\mathrm{Ne}}RT\ln \left[\frac{T^{3}V}{N_{\mathrm{Ne}}}\right]$

$F\left[{\mu }_{\mathrm{He}}\right]=-R{T}^{\frac{5}{2}}V{e}^{-(1-\frac{{\mu }_{\mathrm{He}}}{RT})}-N_{\mathrm{Ne}}RT\ln \left[\frac{T^{\frac{3}{2}}V}{N_{\mathrm{Ne}}}\right]$

$p\equiv -{\left(\frac{\partial F[{\mu }_{\mathrm{He}}]}{\partial V}\right)}_{T,{\mu }_{\mathrm{He}},N_{\mathrm{Ne}}}\Rightarrow p=-{\left(\frac{\partial (-R{T}^{\frac{5}{2}}V{e}^{-(1-\frac{{\mu }_{\mathrm{HP}}}{RT})}-N_{\mathrm{Ne}}RT\ln \left[\frac{T^{\frac{3}{2}}V}{N_{\mathrm{Ne}}}\right])}{\partial V}\right)}_{T,{\mu }_{\mathrm{He}}}\Rightarrow$

$p=R{T}^{\frac{5}{2}}{e}^{-(1-\frac{{\mu }_{\mathrm{He}}}{RT})}+\left[\frac{N_{\mathrm{Ne}}RT}{V}\right]$

$p=p(T,V,{\mu }_{\mathrm{He}},N_{\mathrm{Ne}})\Rightarrow {\left(\frac{\partial p}{\partial V}\right)}_{T,{\mu }_{\mathrm{He}},N_{\mathrm{Ne}}}=-\frac{V^2}{N_{\mathrm{Ne}}RT}\Rightarrow -\frac{1}{V}{\left(\frac{\partial V}{\partial p}\right)}_{T,{\mu }_{\mathrm{He}},N_{\mathrm{Ne}}}=\frac{V^2}{N_{\mathrm{Ne}}RT}\Rightarrow$

$-\frac{1}{V}{\left(\frac{\partial V}{\partial p}\right)}_{T,{\mu }_{\mathrm{He}},N_{\mathrm{Ne}}}=\frac{1}{p_{\mathrm{Ne}}}$

---

Testuingurua

40. ARIKETA

Aurreko ariketako zilindroa Ne gasa erabiliz bete dugu: $\frac{1}{10}$ mol sartuz. Zilindroaren beheko horma ez da neonarekiko iragazkorra.

Lortu zilindroko presioaren balioa eta sistemaren konprimigarritasuna.

(C 7.4.19)

Emaitza

Ebazpen posible bat…

---

Ondorengo bi ariketak modu berean abatzi behar dira. Lehenengo eta behin, ebaztean erabiliko diren aldagaiak finkatu behar dira; printzipioz, enuntziatuek berek finkatuko dute: bien kasuan, $p/v$ diagraman gertatuko den prozesua dugu; beraz, aldagai independenteak $p$ eta $v$ dira. Gainera, bietan ere bai, prozesua bera nola gertatuko den ere aipatuta dago: $p/v$ diagramako kurba baten adierazpenaren bidez; hots, aldagaien arteko lotura baten bidez (aldakuntzak ere lotuta daude). Beraz, aldagaietatik bat baino ez da independentea, gure esku dago zein. Horrez gain, ariketa bietan, hasierako zein bukaerako oreka-egoerak ezagunak dira: $A$ eta $B$ etiketen bidez adierazita. Azkenik, $A$ eta $B$ egoerak lotuko dituen kurban zehar ezagunak dira $(c_p,\alpha ,{\kappa }_T)$ sortako koefiziente esperimentalak; orduan, kalkulu termodinamikoaren bidez lortuko ditugun adierazpenetan ezagunak diren funtzioak ordezkatu ondoren, integrazioz, kalkulatu beharreko parametroen aldakuntzak lortu ahal izango ditugu.

Prozedura laburbilduz:

1. Identifikatu aldagai independenteak

2. Identifikatu hasierako eta bukaerako oreka-egoerak

3. Identifikatu prozesuaren adierazpena: aldagai independenteen arteko lotura Lortu aldagien aldakuntza diferentzialen arteko lotura

4. Identifikatu kalkulatu beharreko koefizientea Kalkulatu koefizientea: lortu adierazpen orokorra

5. Ordezkatu adierazpen orokorrean enuntziatuko datuak Integratu

Testuingurua

41. ARIKETA

Esku artean substantzia baten mol bakarra dugu. $p/V$ diagramako A eta B puntuak $p{v}^2=\mathrm{k}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{a}$ lerroko puntuak dira. Aipatutako lerroan zehar ezagunak dira sistemaren ondoko ezaugarriak: $C_p=C{v}^2$, $\alpha =\frac{D}{v}$ eta ${\kappa }_T=Ev$. $C$, $D$ eta $E$ konstanteak dira.

Lortu $T_B$ tenperatura ($T_A$, $p_A$, $v_A$, $v_B$, $C$, $D$, $E$) sortaren funtzioan.

(C 7.4.20)

Emaitza

Ebazpen posible bat…

1. Identifikatu aldagai independenteak:

   $$p/v\Rightarrow p,v$$

2. Identifikatu hasierako eta bukaerako oreka-egoerak:

   $$\text{ A, }B$$

3. Identifikatu prozesuaren adierazpena: aldagai independenteen arteko lotura Lortu aldagien aldakuntza diferentzialen arteko lotura

   $$\begin{array}{r}\begin{array}{rl}& p{v}^2=\text{ konst. }\Rightarrow v^{2}dp+2pdv=0\Rightarrow \frac{dp}{p}=-2\frac{dv}{v^2}\\ & dp=-2\left(p_A{v}_A^2\right)\frac{dv}{v^3}\end{array}\end{array}$$

4. Identifikatu kalkulatu beharreko koefizientea
   Kalkulatu koefizientea: lortu adierazpen orokorra

   $$\begin{array}{r}\begin{array}{rl}& T=T(p,v)\\ & dT={\left(\frac{\partial T}{\partial p}\right)}_{v}dp+{\left(\frac{\partial T}{\partial v}\right)}_{p}dv\Rightarrow dT=\frac{{\kappa }_T}{\alpha }dp+\frac{1}{v\alpha }dv\end{array}\end{array}$$

5. Ordezkatu adierazpen orokorrean enuntziatuko datuak Integratu

   $$\begin{array}{r}\begin{array}{l}dT=\frac{{\kappa }_T}{\alpha }(-2p_A{v}_A^2\frac{dv}{v^3})+\frac{1}{v\alpha }dv\\ \alpha =\frac{D}{v}\\ {\kappa }_T=Ev\end{array}\}\Rightarrow dT=\frac{Ev}{\left(\frac{D}{v}\right)}(-2p_A{v}_A^2\frac{dv}{v^3})+\frac{1}{v\left(\frac{D}{v}\right)}dv\Rightarrow \end{array}$$
   $$dT=-\frac{2E}{D}{p}_A{v}_A^2\frac{dv}{v}+\frac{1}{D}dv\Rightarrow dT=\{-\frac{2E}{D}{p}_A{v}_A^2\frac{1}{v}+\frac{1}{D}\}dv\Rightarrow \int dT=\int \{-\frac{2E}{D}{p}_A{v}_A^2\frac{1}{v}+\frac{1}{D}\}dv\Rightarrow$$
   $$\mathrm{\Delta }T=-\frac{2E}{D}{p}_A{v}_A^2\ln \frac{v_B}{v_A}+\frac{1}{D}(v_B-v_A)\Rightarrow \boxed{{\displaystyle T_B=T_A-\frac{2E}{D}{p}_A{v}_A^2\ln \frac{v_B}{v_A}+\frac{1}{D}(v_B-v_A)}}$$

---

Testuingurua

42. ARIKETA

Esku artean substantzia baten mol bakarra dugu. $p/V$ diagramako A eta B puntuak $pv=\mathrm{k}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{a}$ lerroko puntuak dira. Aipatu lerroan zehar ezagunak dira sistemaren ondoko ezaugarriak: $C_p=Cv$, $\alpha =\frac{D}{v^2}$ eta ${\kappa }_T=Ev$. $C$, $D$ eta $E$ konstanteak dira.

Lortu ($u_A-u_B$) kendura ($T_A$, $p_A$, $v_A$, $v_B$, $C$, $D$, $E$) sortaren funtzioan.

(C 7.4.21)

Emaitza

Ebazpen posible bat…

1. Identifikatu aldagai independenteak:

   $$p/v\Rightarrow p,v$$

2. Identifikatu hasierako eta bukaerako oreka-egoerak:

   $$A,B$$

3. Identifikatu prozesuaren adierazpena: aldagai independenteen arteko lotura Lortu aldagien aldakuntza diferentzialen arteko lotura

   $$\begin{array}{r}\begin{array}{rl}& pv=\text{ konst. }\Rightarrow vdp+pdv=0\Rightarrow \frac{dp}{p}=-\frac{dv}{v}\\ & dp=-2\left(p_A{v}_A\right)\frac{dv}{v^2}\end{array}\end{array}$$

4. Identifikatu kalkulatu beharreko koefizientea
   Kalkulatu koefizientea: lortu adierazpen orokorra

   $$u=u(p,v)\Rightarrow du={\left(\frac{\partial u}{\partial p}\right)}_{v}dp+{\left(\frac{\partial u}{\partial v}\right)}_{p}dv$$
   $$du=Tds-pdv$$
   $$\begin{array}{r}\begin{array}{l}{\left(\frac{\partial u}{\partial p}\right)}_v={\left(\frac{\partial (Tds-pdv)}{\partial p}\right)}_v=T{\left(\frac{\partial s}{\partial p}\right)}_v-p{\left(\frac{\partial v}{\partial p}\right)}_v=T{\left(\frac{\partial s}{\partial T}\right)}_v{\left(\frac{\partial T}{\partial p}\right)}_v=c_V\frac{{\kappa }_T}{\alpha }\\ {\left(\frac{\partial u}{\partial v}\right)}_p={\left(\frac{\partial (Tds-pdv)}{\partial v}\right)}_p=T{\left(\frac{\partial s}{\partial v}\right)}_p-p{\left(\frac{\partial v}{\partial v}\right)}_p=T{\left(\frac{\partial s}{\partial T}\right)}_p{\left(\frac{\partial T}{\partial v}\right)}_p-p=c_p\frac{1}{v\alpha }-p\end{array}\}\Rightarrow \end{array}$$
   $$du=\left(c_V\frac{{\kappa }_T}{\alpha }\right)dp+(c_p\frac{1}{v\alpha }-p)dv$$

5. Ordezkatu adierazpen orokorrrean enuntziatuko datuak
   Integratu

   $$\begin{array}{r}\begin{array}{rl}& du=\left(c_V\frac{{\kappa }_T}{\alpha }\right)(-p_A{v}_A\frac{dv}{v^2})+(c_p\frac{1}{v\alpha }-p)dv\Rightarrow du=\left(c_V\frac{{\kappa }_T}{\alpha }\right)(-p_A{v}_A\frac{dv}{v^2})+(c_p\frac{1}{v\alpha }-p)dv\\ & \\ & \begin{array}{rl}& \begin{array}{c}\alpha =\frac{D}{v^2}\\ {\kappa }_T=Ev\end{array}\}\Rightarrow \frac{{\kappa }_T}{\alpha }=\frac{(Ev)}{\left(\frac{D}{v^2}\right)}=\frac{E}{D}{v}^3\\ & c_p=Cv\\ & c_p-c_V=\frac{Tv{\alpha }^2}{{\kappa }_T}\Rightarrow c_V=c_p-\frac{Tv{\alpha }^2}{{\kappa }_T}\end{array}\}\Rightarrow c_V=Cv-\frac{Tv{\left(\frac{D}{v^2}\right)}^2}{(Ev)}\Rightarrow c_V=Cv-T{\left(\frac{D}{E}\right)}^2\frac{1}{v^5}& \\ & \end{array}\}\Rightarrow \end{array}$$

$$du=\left(c_V\frac{{\kappa }_T}{\alpha }\right)(-p_A{v}_A\frac{dv}{v^2})+(c_p\frac{1}{v\alpha }-p)dv$$

$$du=\left\{(Cv-Tv\frac{1}{Ev}{\left(\frac{D}{v^2}\right)}^2)\left(\frac{E}{D}{v}^3\right)\right\}(-p_A{v}_A)\frac{dv}{v^2}+(Cv\frac{1}{v\left(\frac{D}{v^2}\right)}-\frac{p_A{v}_A}{v})dv$$

$$du=\left\{(\frac{CE}{D}{v}^2-T\frac{1}{v^3}D)\right\}(-p_A{v}_A)dv+(\frac{C}{D}{v}^2-\frac{p_A{v}_A}{v})dv$$

$$du=(\frac{C}{D}(1-p_A{v}_{A}E)v^2+TD{p}_A{v}_A\frac{1}{v^3}-\frac{p_A{v}_A}{v})dv$$

$$dT=\frac{{\kappa }_T}{\alpha }(-p_A{v}_A\frac{dv}{v^2})+\frac{1}{v\alpha }dv$$

$$dT=\frac{E}{D}{v}^3(-p_A{v}_A\frac{dv}{v^2})+\frac{1}{v\left(\frac{D}{v^2}\right)}dv\Rightarrow dT=-p_A{v}_A\frac{E}{D}vdv+\frac{1}{D}vdv\Rightarrow dT=(1-p_A{v}_{A}E)\frac{1}{D}vdv\Rightarrow$$

$$\int dT=\int (1-p_A{v}_{A}E)\frac{1}{D}vdv\Rightarrow T=(1-p_A{v}_{A}E)\frac{1}{D}{v}^2\Rightarrow$$

$$du=\{\frac{C}{D}(1-p_A{v}_{A}E)v^2+\left((1-p_A{v}_{A}E)\frac{1}{D}{v}^2\right)D_A{v}_A\frac{1}{v^3}-\frac{p_A{v}_A}{v}\}dv$$

---

Testuingurua

43. ARIKETA

Esku artean dugun sistemaren kasuan, $p/v$ diagramako lerro zuzenean zeharreko espantsioak ($p_0$, $v_0$) eta ($p_f$, $v_f$) egoerak lotu ditu. ($c_p$, $\alpha$, ${\kappa }_T$) sortako parametroak $v=v_0$ lerro isokoroan zehar eta $p=p_f$ lerro isobaroan zehar soilik ezagunak dira; $\frac{c_v{\kappa }_T}{\alpha }=Ap$ $(v=v_0)$, $\frac{c_p}{v\alpha }=Bv$ $(p=p_f)$.

Lortu prozesuan trukaturiko beroa.

(C 7.4.23)

Emaitza

$Q=\frac{1}{2}A(p_f^2-p_0^2)+\frac{1}{2}B(v_f^2-v_0^2)+\frac{1}{2}(p_0-p_f)(v_f-v_0)$

Ebazpen posible bat…

---

Testuingurua

44. ARIKETA

Aztertuko dugun sistema alboko irudian ageri da; 1 eta 2 zilindroek osatu dute. Irudian ikus daitekeenez, lehenengoa bigarrenaren barnean higi daiteke. Bien artean ez dago marruskadurarik. Marrazturiko hormak adiabatikoak dira eta besteak, aldiz, diatermoak. Hasiera batean sistema osoa oreka-egoeran dago. 1 zilindroa $T$ tenperaturako eta $p$ presioko iturriarekin ukipenean jarri dugu. Efizientzia maximoko punpa dugu, zeinak eskura dugun iturritik beroa ateraz, 1 zilindrotik ateratako bero osoa 2 zilindroari emango dion. Prozesu horrek iturriarekiko oreka lortu arte iraungo du.

Lortu:

1. zilindroen bukaerako tenperaturak eta 2 zilindroaren bukaerako bolumena,

2. bi sistemetako entropia-aldaketak,

3. punpak egindako lana eta

4. inguruneari dagokion entropia-aldaketa.

5. Eztabaidatu kualitatiboki zenbatekoa izango den sistema osoaren entropia-aldaketa.

Emaitza

Ebazpen posible bat…

---

Testuingurua

45. ARIKETA

Aztertu beharreko sistema honako hau da: $V$ bolumeneko tangan dauden, $T\approx 0$ K tenperaturan, $s=\frac{1}{2}$ spineko partikulak (esaterako, metaletako tenperatura txikietako elektroiz osatutako gas ideala).

Sistemari dagokion oinarrizko ekuazioa honako hau da:

$$U=\frac{3}{5}A{N}^{\frac{5}{3}}{V}^{-\frac{2}{3}}[1+\frac{5}{3}{\left(\frac{S}{\pi NR}\right)}^2]$$

$A$ da konstante positiboa.

Lortu honako hauek:

1. $F$ potentzial termodinamikoa

2. $p$ presioa, ($S,V$) eta ($T,V$) aldagai-sorten funtzioan

3. $C_V$ bolumen konstanteko bero-ahalmena

Emaitza

Ebazpen posible bat…

---

Testuingurua

46. ARIKETA

Aztertu beharreko sistemari dagokion oinarrizko ekuazioa honako hau da:

$$F=-A{N}^{\frac{2}{3}}{V}^{\frac{1}{3}}{T}^2$$

$A$ konstante positiboa da.

Sistemaren bolumena zortzi aldiz handitu dion zabaltze adiabatiko itzulgarriaren ondorioz, zenbatekoa da tenperatura-aldaketa?

Emaitza

Ebazpen posible bat…

---

Testuingurua

47. ARIKETA

Erraztu honako adierazpen hau:

$${\left(\frac{\partial T}{\partial p}\right)}_H$$

Koefiziente horri Joule-ren eta Kelvin-en koefiziente deritzo, ${\mu }_{J-K}$.

Emaitza

Ebazpen posible bat…

---

Testuingurua

48. ARIKETA

Aztertu beharreko sistemari dagozkion bi egoerak, $p/v$ planokoak haiek, honako hauek dira:

1. $p_A={10}^5$ Pa., $v_A=2\times {10}^{-2}$ $\frac{{\text{m}}^3}{\text{mol}}$, $T_A=350.9$ K

2. $p_B={10}^4$ Pa., $v_B={10}^{-1}$ $\frac{{\text{m}}^3}{\text{mol}}$

$A$ egoeratik $B$ egoerara eramndakoan sistema, zenbatekoa da lor daitekeen lan maximoa? Prozesua aurrera eramateko, erabilgarria da $150$ Ketan dagoen bero-iturria.

Ezagunak dira baita ere honako datua hauek:

1. lerro adiabatiko itzulgarrien adierazpena: $p{v}^2=k$

2. presio konstantean, $p=p_A$: $c_p=D{v}^{\frac{2}{3}}$

3. presio konstantean, $p=p_A$: $\alpha =\frac{3}{T}$

4. $D={10}^{\frac{3}{8}}$ $\frac{\text{J}}{{\text{m}}^{2}K}$

Emaitza

Ebazpen posible bat…

---