The 2nd Law

---

1 NATURE’S DISSYMMETRY

War and the steam engine joined forces and forged what was to become one of the most delicate of concepts. Sadi Carnot, the son of a minister of war under Napoleon and the uncle of a later president of the Republic, fought in the outskirts of Paris in 1814. In the turmoil that followed, he formed the opinion that one cause of France’s defeat had been her industrial inferiority. The contrast between England’s and France’s use of steam epitomized the difference. He saw that taking away England’s steam engine would remove the heart of her military power. Gone would be her coal, for the mines would no longer be pumped. Gone would be her iron, for, with wood in short supply, coal was essential to ironmaking. Gone, then, would be her armaments.

But Carnot also perceived that whoever possessed efficient steam power would be not only the industrial and master of the world, but also the leader of a social revolution far more universal than the France had so recently undergone. Carnot saw steam power as a universal motor. This motor would displace animals because of its greater economy and would supersede wind and water because of its reliability and its controllability. Carnot saw that the universal motor would enlarge humanity’s social and economic horizons, and carry it into a new world of achievement. Many people today can see the early steam engines, those cumbersome hulks of wood and iron, only as ponderous symbols of the squalor and poverty that typified the newly emerging industrial society. In fact, those earthbound leviathans proved to be the wings of humanity’s aspirations.

Carnot was a visionary and a sharp analyst of what was needed to improve the steam engine (as his father had been an acute analyst of mechanical devices), but he could have had no inkling of the intellectual revolution to which his technologically motivated studies would lead. In discovering that there is an intrinsic inefficiency in the conversion of heat into work, he set in motion an intellectual mechanism which a century and a half later embraces all activity. In pinning down the efficiency of the steam engine and circumscribing its limitations, Carnot was unconsciously establishing a new attitude toward all kinds of change, toward the conversion of the energy stored in coal into mechanical effort, and even toward the unfolding of a leaf. Moreover, he was also establishing a science that went beyond the apparently abstract physics of Newton, one that could deal with both the abstractions of single particles and the reality of engines. All this encapsulates the span of topics in this book: we shall travel from the apparently coarse world of the early industrial engine to the delicate and refined world of the enjoyment of beauty, and in doing so we shall discover them one.

On of the earliest steam engines. Its analysis stimated the ideas we explore in this book.

Carnot’s work (which was summarized in his Refléxions sur la puissance motrice du feu, published in 1824) was based on a misconception; yet, even so, it laid the foundations of our subject. Carnot subscribed to the then-conventional theory that heat was some kind of massless fluid or caloric. He took the view that the operation of a steam engine was akin to the operation of a water mill, that caloric ran from the boiler to the condenser, and drove the shafts of industry as it ran, exactly as water runs and drives a mill. Just as the quantity of water remains unchanged as it flows through the mill in the course of doing its work so (Carnot believed) the quantity of caloric remained unchanged as it did its (Carnot believed) the quantity analysis on the assumption that the quantity of heat was conserved, and that work was generated by the engine because the fluid flowed from a hot, thermally “high” source to a cold, thermally “low” sink.

The intellectual effort needed to disentangle the truth from this misconception had to await a new generation of minds. Among the generation born around 1820, there were three people who would take up the challenge and resolve the confusion.

The Identification of Energy

The first of these three was J. P. Joule, born in 1818. Joule was the son of a Manchester brewer. His wealth, and the brewery’s workshops, gave him the opportunity to follow his inclinations. One such inclination was to discover a general, unifying theme that would explain all the phenomena then exciting scientific attention, such as electricity, electrochemistry, and the processes involving heat and mechanics. His careful experiments, done in the 1840s, confirmed that heat was not conserved. Joule showed by increasingly precise measurements that work could be converted quantitatively into heat. This was the birth of the concept of the mechanical equivalence of heat, that work and heat are mutually interconvertible, and that heat is not a substance like water.

James Prescott Joule (1818-1889)

Such was the experimental evidence that upset the basis for the conclusions, but not the conclusions themselves, that Carnot had drawn a generation before. Now it was time for the theoreticians to take up the challenge and to resolve the nature of heat.

William Thomson, Lord Kelvin (1824-1907)

William Thomson was born in Belfast in 1824, moved to Glasgow in 1832, and entered the university there at age ten, already displaying the intellectual vigor that was to be the hallmark of his life. Although primarily a theoretician, he had great practical ability. Indeed, his wealth sprang from a practical talent, which he polished by a brief sojourn in Paris after he graduated from Cambridge, where he had gone in 1843. His career at Glasgow resumed in 1846, when at 22 he was appointed to the chair of natural philosophy. He divided his time between theoretical analysis of the highest quality and moneymaking of enviable proportions from his work in telegraphy. Great Britain’s preeminence in the field of international communication and submarine telegraphy can be traced to Thomson’s analysis of the problems of transmitting signals over great distances, and his invention (and patenting) of a receiver that became the standard in all telegraph that became the standard in all telegraph offices.

William Thomson, as is sometimes the confusing habit of the British, later matured into Lord Kelvin, by which name we shall refer to him from now on. His wealth and his practical attainments have now been largely forgotten. What remains as his lasting memorial, apart from a slab in Westminster Abbey, is his intellectual achievement.

Kelvin and Joule met at the Oxford meeting of the British Association for the Advancement of Science in 1847. From that meeting Kelvin returned with an unsettled mind. He was reported as being astounded by Joule’s refutation of the conservation of heat. Although impressed with what Joule had been able to demonstrate, he believed that Carnot’s work would be overthrown if heat were not conserved, and if there were no such thing as caloric fluid.

Kelvin began by setting forth the conceptual tangle that appeared to be confronting physics. He went on to develop the view (published in his paper On the dynamical theory of heat in 1851) that perhaps two laws were lurking beneath the surface of experience, and that in some sense the work of Carnot could survive without contradicting the work of Joule. Thus emerged the study, and the name, of thermodymamics, the theory of the mechanical action of heat, and the beginnings of the realization that Nature had to pivots of action.

The third significant mind born in the decade of the 1820s was that of Rudolf Gottlieb. Few students of thermodynamics know this name, for Gottlieb adopted a classical name, as was then a popular affectation. We, henceforth, shall refer to him as Clausius, the name by which he is universally known.

Rudolf Clausius (1822-1888)

Clausius was born in 1822. There should be nothing surprising in the fact that these three shapers of thermodynamics were contemporaries. Thermodynamics was the object of intellectual ferment of the time, and bright minds are attracted to bright possibilities. Clausius’s first contribution cut closer to the bone than had Kelvin’s. In dealing with the theme inspired by Carnot, carried on by Joule, and extended by Kelvin, in a monograph that was titled Über die bewegende Kraft der Wärme when it was published in 1850, Clausius sharply circumscribed the problems then facing thermodynamics, and in doing so made them more open to analysis. His was the focusing mind, the microscope to Kelvin’s cosmic telescope.

Clausius also saw that the case of Carnot vs. Joule could to some extent be resolved if there were two underlying principles of Nature. He refined Carnot’s principle, and rid the world of caloric, but he went further: although he carefully insulated his general conclusions from his speculations, he did go on to speculate on how heat could be explained in terms of the behavior of the particles of which matter is composed. That was the dawn of the modern era of thermodynamics.

Carnot was born in 1796 and died of cholera in 1832; by then he had let slip his belief in the reality of caloric. Joule, Kelvin, and Clausius were born in the period 1818-1824, and their generation thrust thermodynamics onto the intellectual stage. But it needed a third generation to unify this new discipline, and to attach it to the other currents of science which by then were starting to flow.

Ludwig Boltzmann was born in 1844. His contribution was to forge the link between the properties of matter in bulk, then being established by the deployment of Kelvin’s and Clausius’s thermodynamics, and the behavior of matter’s individual particles, its atoms. Kelvin, Clausius, and their contemporaries developed the seed planted by Carnot, and were able to establish a great warehouse of relations between observations. However, comprehension of these relations could come only when a mechanistic explanation in terms of particles and their properties had been established.

Boltzmann perceived that identifying the cooperation between atoms which showed itself to the observer as the properties of bulk matter would take him into the innermost workings of Nature. Though short-sighted, he saw further into the workings of the world than most of his contemporaries, and he began to discover the deep structure of change; furthermore, he did all this before the existence of atoms was generally accepted. Many of his contemporaries doubted the credibility of his assumptions and his argument, and feared that his work would dethrone the purposiveness which they presumed to exist within the workings of the deeper world of change, just as Darwin had recently dispossessed its outer manifestations. unhappiness and killed himself.

In 1906, when Boltzmann died, ideas were in the air, and techniques were becoming available, that were to win over his critics and to establish his reputation as one of the greatest of theoretical physicists. The emergence of quantum theory, together with the experimental exploration and detailed mapping of the structures of atoms, brought to the microscopic world a reality that, although out of joint with the familiar, was compelling and essentially indisputable. When that had been achieved, no one could seriously deny the existence of atoms, even though they appear to behave in a manner that at first sight (and still to some) seemed strange. Now we have techniques that show both individual atoms (below) and atoms strung together into molecules (on right). The fundamental basis of Boltzmann’s viewpoint has been established beyond reasonable doubt, even though that microscopic world is far more peculiar than even he envisaged.

A photograph of atmos, (specifically of zirconium and oxygen in zirconia).

A computer-generated image of fragments of DNA, the genetic coding molecule in the nuclei of cells.

The aims adopted and the attitudes struck by Carnot and by Boltzmann epitomize thermodynamics. Carnot traveled toward thermodynamics from the direction of the engine, then the symbol of industrialized society: his aim was to improve its efficiency. Boltzmann traveled to thermodynamics from the atom, the symbol of emerging scientific fundamentalism: his aim was to increase our comprehension of the world at the deepest levels then conceived. Thermodynamics still has both aspects, and reflects complementary aims, attitudes, and applications. It grew out of coarse machinery; yet it has been refined to an instrument of great delicacy. It spans the whole range of human enterprise, covering the organization and deployment of both resources and ideas, particularly ideas about the nature of change in the world around us. Few contributions to human understanding are richer than this child of the steam engine and the atom.

The Laws of Thermodynamics

The name thermodynamics is a blunderbuss term originally denoting the study of heat, but now extended to include the study of the transformations of energy in all its forms. It is based on a few statements that constitute succinct summaries of people’s experiences with the way that energy behaves in the course of its transformations. These summaries are the Laws of thermodynamics. Although we shall be primarily concerned with just one of these laws, it will be useful to have at least a passing familiarity with them all.

There are four Laws. The third of them, the Second Law, was recognized first; the first, the Zeroth Law, was formulated last; the First Law was second; the Third Law might not even be a law in the same sense as the others. Happily, the content of the laws is simpler than their chronology, which represents the difficulty of establishing properties of intangibles.

The Zeroth Law was a kind of logical afterthought. Formulated by about 1931, it deals with the possibility of defining the temperature of things. Temperature is one of the deepest concepts of thermodynamics, and I hope this book will sharpen your insight into its elusive nature. As time is the central variable in the field of physics called dynamics, so temperature is the central variable in thermodynamics. Indeed, there are several amusing analogies between time and temperature that go deeper than the accidents that they both begin with and are represented by the same letter. For now, however, we shall regard temperature as a refinement and quantitative expression of the everyday notion of “hotness”.

The First Law is popularly stated as “Energy is conserved”. That it is energy which is conserved, not heat, was the key realization of the 1850 s, and the one that Kelvin and Clausius presented to the world. Indeed, the emergence of energy as a unifying concept was a major achievement of nineteenth-century science: here was a truly abstract concept coming into a dominant place in physics. Energy displaced from centrality the apparently more tangible concept of “force”, which had been regarded as the unifying concept ever since Newton had shown how to handle it mathematically a century and a half previously.

Energy is a word so familiar to us today that we can hardly grasp either the intellectual Everest it represents or the conceptual difficulty we face in saying exactly what it means. (We face the same difficulty with “charge” and “spin” and other fundamental familiarities of everyday language.) For now, we shall assume the concept of energy is intuitively obvious, and is conveyed adequately by its definition as “the capacity to do work”. The shift in the primacy of energy can be dated fairly accurately. In 1846 Kelvin was arguing that physics was the science of force. In 1847 he met and listened to Joule. In 1851 he adopted the view that, after all, physics was the science of energy. Although forces could come and go, energy was here to stay. This concept appealed deeply to Kelvin’s religious inclinations: God, he could now argue, endowed the world at the creation with a store of energy, and that divine gift would persist for eternity, while the ephemeral forces danced to the music of time and spun the transitory phenomena of the world.*

• A mischievous cosmologist might now turn this argument on its head. One version of the Big Bang, the inflationary scenario, can be interpreted as meaning that the total energy of the Universe is indeed constant, but constant at zero! The positive energy of the Universe (largely represented by the energy equivalent of the mass of the particles present, that is, by the relation $E=m{c}^2$ ) might exactly balance the negative energy (the gravitational attractive potential energy), so that overall the total might be zero. Thus Kelvin’s God may have left a nugatory legacy.

Kelvin hoped to raise the concept of energy beyond what it was becoming in the hands of the mid-nineteeth-century physicists, a mere constraint on the changes that a collection of particles could undergo without injection of more energy from outside. He hoped to establish a physics based solely on energy, one free of allusions to underlying models. He had a vision that all phenomena could be explained in terms of the transformations of energy, and that atoms and other notions were to be regarded merely as manifestations of energy. To some extent modern physics appears to be confirming his views, but it is doing so in its typical slippery way: without doing away with atoms!

The Second Law recognizes that there is a fundamental dissymmetry in Nature: the rest of this book is focused on that dissymmetry, and so we shall say little of it here. All around us, though, are aspects of the dissymmetry: hot objects cool, but cool objects do not spontaneously become hot; a bouncing ball comes to rest, but a stationary ball does not spontaneously begin to bounce. Here is the feature of Nature that both Kelvin and Clausius disentangled from the conservation of energy: although the total quantity of energy must be conserved in any process (which is their revised version of what Carnot had taken to be the conservation of the quantity of caloric), the distribution of that energy changes in an irreversible manner. The Second Law is concerned with the natural direction of change of the distribution of energy, something that is quite independent of its total energy.

The Third Law of thermodynamics deals with the properties of matter at very low temperatures. It states that we cannot bring matter to a temperature of absolute zero in a finite number of steps. As I said earlier, the Third Law might not be a true Law of thermodynamics, because it seems to assume that matter is atomic, whereas the other Laws are summaries of direct experience and are independent of any such assumption. There is thus a difference of kind between this Law and the others, and even its logical implications seem less securely founded than theirs. We shall touch on it again, but only much later.

These, then, in broad and indistinct outline, are the Laws that stake out our domain: we have identified the territory; we shall proceed to explore its details. The Laws present us, however, with an immediate problem: thermodynamics is an intrinsically mathematical subject. Clausius’s remarkably elegant functional thermodynamics is a collection of mathematical relations between observations; but with the relations gone, so too is the subject. Boltzmann’s beautiful statistical thermodynamics (some of which is carved on his tombstone) also consists of its equations; without them, we the principal reason why it remains so daunting. the principal reason why it remains so daunting.

Nevertheless, the subject is so important, and the implications of the Second Law so profound and far-reaching, that it seems worth the effort to discover a loophole in its mathematical defenses. What we shall do in the following pages, therefore, is attempt to explore thermodynamics without the mathematics. Then we shall not have the pain (a pain that many rightly regard as at least half the pleasure) of the mathematics. Although we shall necessarily remain outside the subject itself, we shall be able to share the insights it provides into the workings of the world.

But shall we remain so very much outside? Shall we be merely outsiders, tourists, while the real activities go on inside? A more optimistic attitude (and one applicable to other fields as well) is to take the view that mathematics is only a guide to understanding, a refiner of arguments and a purifier of comprehension, and not the endpoint of explanation. If that is so, then the people within are the unlucky toilers who are merely working to sharpen our wits. Whichever position you adopt, I hope the following pages will add something to your view of the world.

Revolutions of Dissymmetry

An intrinsic dissymmetry of Nature is reflected in our technological history. The conversion of stored energy and of work into heat has been commonplace for thousands of years. However, the widespread mastery of the reverse, the controlled conversion of heat and stored energy into work; dates principally from the industrial revolution. I say “principally” because work has, of course, been achieved for centuries. The conversion of wind which is essentially a store of energy supplied by the Sun-into the motion of mills and ships is one example of such a conversion. The use of animals is another, even more indirect procedure with the same overall result. But we can regard the industrial revolution as the surge of activity released by humanity’s sudden discovery of how to exploit energy, how to convert heat into work at will, so that changes in society were no longer limited by using animals to do work and by the one-sided processes of Nature.

Primitive people learned to produce heat at will and in abundance by burning fuels. Then, apart from reliance on such natural sources as winds and oxen, it took people thousands of years to discover the much more sophisticated procedures by which the energy in fuels could be converted into work (other than by feeding the fuels as food to cattle, horses, and slaves). The founders of the industrial revolution mastered the production of work in abundance and at will.

An open hearth is a primitive way of realising the energy stored in fuels.

On the other hand, a jet engine, which extracts the energy of fuels as work, is much more complicated.

The differences in the degrees of sophistication needed to produce heat, on the one hand, and work, on the other, from the same fuel are apparent as soon as we look at the equipment each process requires. In order to produce heat from a fuel, all we need is an open hearth (below), on which the unconstrained combustion of the fuel-wood, coal, or animal and vegetable oils-produces more or less abundant heat. In order to achieve work, we need a much more complicated device (above). Primitive people used the heat of their simple hearths to unlock the elements from the Earth, and from them gradually built the basis of civilization.

Although early minds were unaware of it, what their fires were releasing was the energy trapped from the Sun. (It is fitting, but coincidental. that many should have worshipped the Sun too.) At first the demands on civilization were slight, and could be satisfied by the energy which the sun had shone down in recent years, and which had been stored in the annul growth of vegetation. But as civilization progressed, trapped solar energ that had been accumulated in former ages was increasingly exploited, and wood gave way to coal as the principal fuel. Nevertheless, this was not 2 technological revolution, for all that was happening was that people were mining further back in time, and retrieving the energy trapped from the Sun in an earlier epoch.

Modern civilizations continue this quest to mine the past for the har vest laid down in earlier times. Now we exploit the great stores of oil, the partially decayed remnants of marine life (which also drew its initial sustenance from the Sun). But such are our demands that we have been forced to dig beyond that time and collect the harvest of other stars. For example, the atoms of uranium we now burn in the complex hearths of nuclear reactors are the rich ashes of former stars. These atoms were formed in the death throes of early generations of stars, when light atoms were hurled against each other with such energy that they fused into progressively heavier ones. The old stars exploded, sloughing off the atoms and spreading them through space, to go through other roastings, explosions, and dispersals, until in due course they collected in the ball of rock we stand on and mine today.

But the quest for fire from the past goes on even deeper. Now we seek to mine beyond the formation of the Earth, beyond the deaths of generations of stars, and into the ash of the creation itself.

In the earliest moments of the Universe, the Big Bang shook spacetime to its foundations, and conditions of almost inconceivable tumult raged through the swelling cosmos; yet this great cataclysm managed to produce only the simplest atoms of all. The labor of the cosmic elephant resulted in the birth of a cosmic mouse: out from the tumult dropped hydrogen with a dash of helium. These elements, still superabundant, are the ashes of the Big Bang, and our attempts to achieve the controlled fusion of hydrogen into helium are aimed at capturing the energy they still store. Hydrogen is the oldest fossil fuel of all: when we master fusion, we shall be mining at the beginning of time.

The emergence and flourishing of civilizations has thus been characterized by our mining progressively further into the past for convenient, concentrated supplies of energy. Mining deeper in time, however, is merely an elaboration of the primitive discovery that energy can be unleashed as heat. However sophisticated the hearth, the combustion of fossils, whether of vegetation, stars, or the Big Bang, is merely a linear series of refinements of the basic discovery of combustion. Such refinements are not in themselves revolutions: they are sophistications-qualitative extensions-of processes that are almost as old as the hills.

Without the revolution that comes about from exploring the other side of Nature’s dissymmetry, the conversion of heat into work, we would merely be warmer, not wiser. This other side lets us tap the store of energy in fuel and extract from it motive power. Then, with motive power we can make artifacts, we can travel, and we can even communicate without traveling. Why, though, did this dissymmetry take so long to exploit? The task confronting humanity was to find a way to extract ordered motion from disordered motion, for therein lies the difference between heat and work. This is the moment when we must look more closely at the nature of the dissymmetry, and bring ourselves forward from the time before Carnot to the comprehension that came with Clausius and Kelvin.

The Identification of the Dissymmetry

We shall use a steam engine to identify Nature’s dissymmetry. This is essentially what Carnot did. We shall then step inside the engine, so to speak, and discover the atomic basis of the dissymmetry of events. That is what Clausius identified and Boltzmann developed.

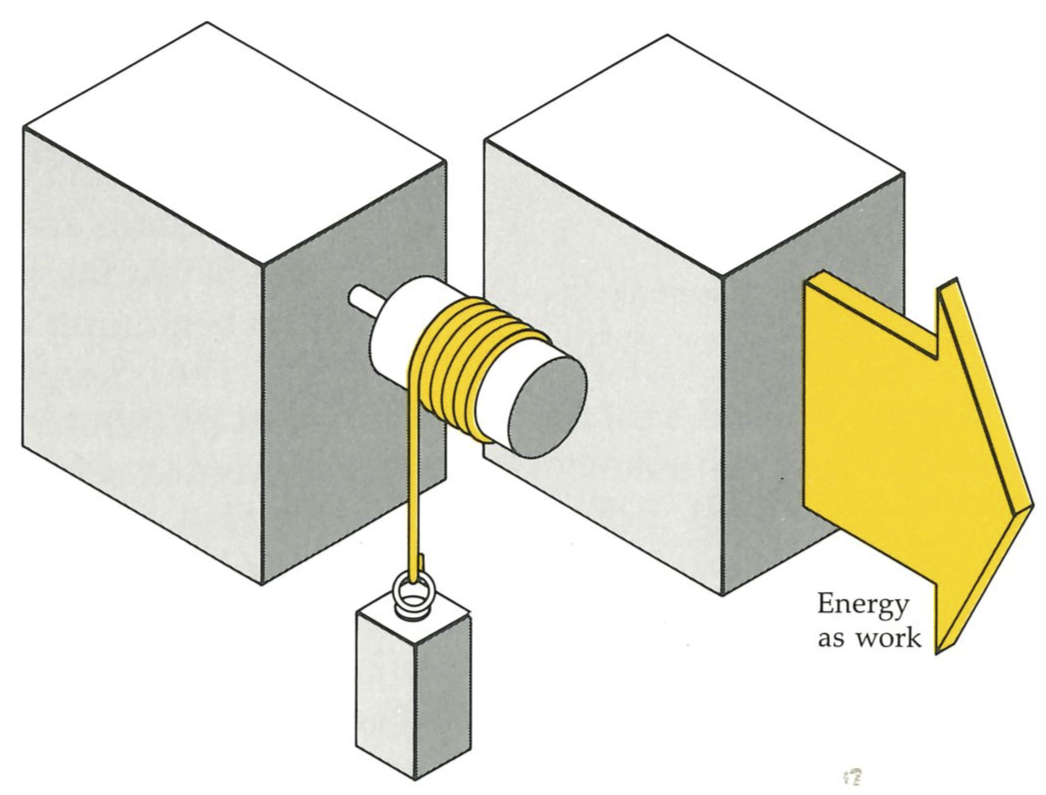
An engine is something that converts heat into work. Work is a process such as raising a weight (below). Indeed, we shall define work as any process that is equivalent to the raising of a weight. Later, as this story develops, we shall use our increased insight to build more general definitions and find the most all-embracing definition right at the end. That is one of the delights of science: the more deeply a concept is understood, the more widely it casts its net. Heat we shall come to later.

Work is a way of transferring energy between a system and its surroundings; it is a transfer effected in such a way that a weight could be raised in the surroundings as a result. When work is done on a system, the change in the surroundings is equivalent to the lowering of a weight.

An engine should be capable of operating indefinitely, and to go on making the conversion for as long as the factory operates or for as long as the journey lasts. Single-shot conversions, such as the propulsion of a cannonball by the combustion of a charge of powder, produce work, but are not engines in this sense. An engine is a device that operates cyclically, and returns periodically (once in each revolution, or once in several revolutions, of a crankshaft, for instance) to its initial condition. Then it can go on, in principle, for ever, living off the energy supplied by the hot source which in turn is supplied with energy by the burning fuel.

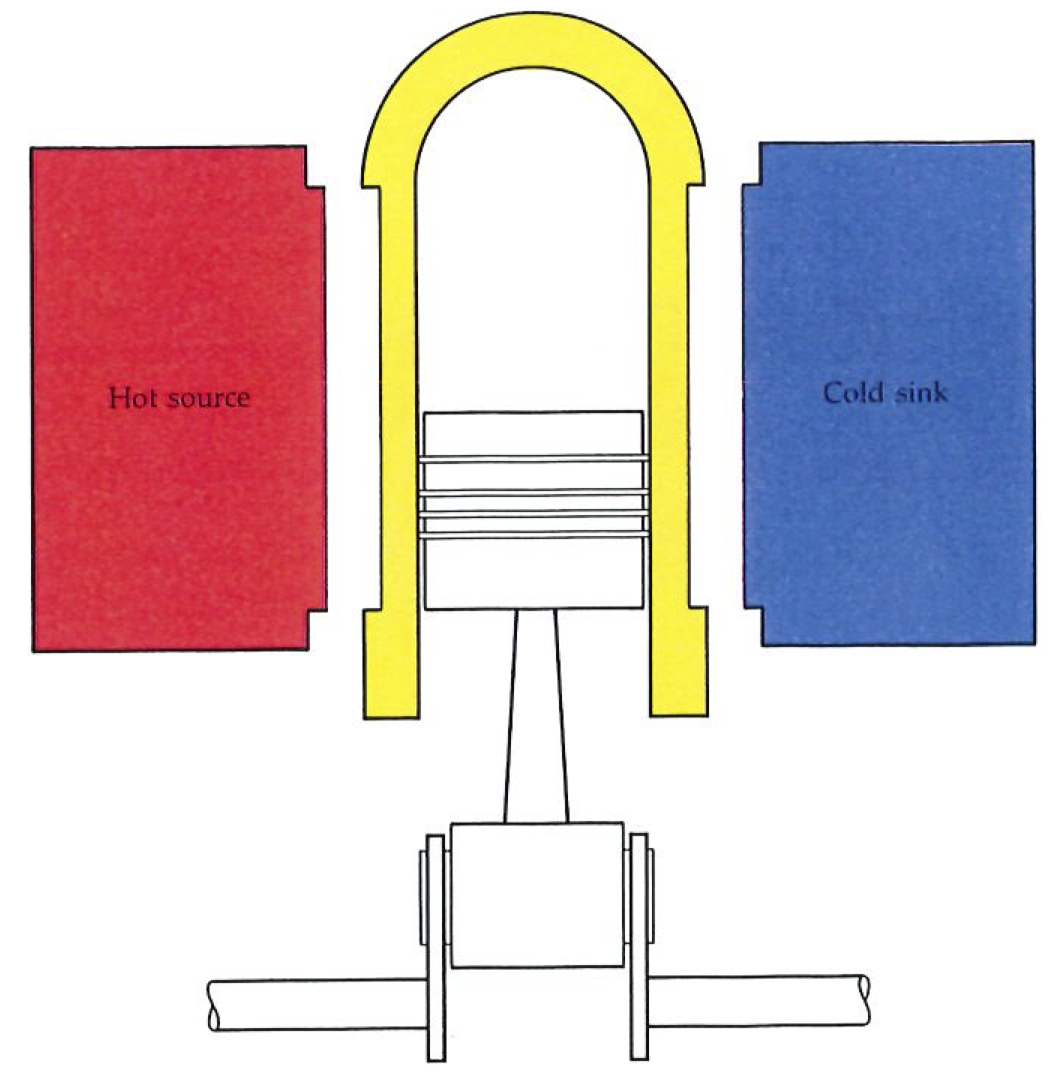
Engines and the cycles they go through in the course of their operation may be as intricate as we please. A sequence of steps known as the Carnot cycle is a convenient starting point. The cycle is an abstract idealization, and very simple. Nevertheless, it may be elaborated (as we shall see later) to reproduce the stages that real engines such as gas turbines and jet engines go through, and it captures the essential feature of all engines. The engine itself (as illustrated below) consists of a gas trapped in a cylinder fitted with a piston. The cylinder can be put in contact with a hot source (steam from a boiler) and with a cold sink (cooling water), or it may be left completely insulated. Note that the operation does not capture the actual working of a steam engine, because in the Carnot engine steam is not admitted directly into the cylinder.

We can follow the course of the engine as it goes through its cycle by following the pressure changes inside the cylinder. A diagram showing the pressure at each stage is called an indicator diagram. Indicator diagrams were used by James Watt, but he kept them a trade secret; the French scientist Emile Clapeyron introduced them into the discussion of the Carnot cycle. Carnot indeed has a deep debt of gratitude to Clapeyron, for not only did the latter refine his cycle, make a mathematical analysis of it, and portray it in terms of an indicator diagram, but it was Clapeyron’s paper “Mémoire sur la puissance motrice du feu” (yet another variation on the theme), published in 1834, that kept Carnot’s work alive and brought it to the attention of others, particularly of Kelvin.

The Carnot engine consists of a working gas confined to a cylinder which may be put in thermal contact with hot or cold reservoirs, or thermally insulated, at various stages of the cycle of operations. Each stage of the cycle is performed quasistatically (infinitely slowly), and in a manner which ensures that the maximum amount of work is extracted. There are no losses arising from turbulence, friction, and so on.

James Watt (1736-1819)

Emile Clapeyron (1799-1864)

In order to follow the engine through its cycle, we need to know some elementary properties of gases. The first is that as a given amount of gas is confined to ever-smaller volumes (as a piston is driven in), then its pressure increases. The magnitude of the increase depends on how the compression is carried out. If the gas is kept in contact with a heat sink (a) thermal reservoir) of some kind (for instance, a water bath or a great block of iron), then its temperature remains the same, and the compression is called isothermal. Under these circumstances the rise in pressure follows one of the curves (isotherms) shown in the figure on the facing page. (These isotherms are mathematically hyperbolas, $p\propto 1/V$, as was established by Rotert Boyle in the mid-seventeenth century; their precise form, however, immaterial to this discussion.) Alternatively, the gas may be thermally insulated (the cylinder wrapped in insulating material). Under these circumstances no heat may leave or enter the gas, and the compression is called adiabatic.

The experimental observation is that during an adiabatic commpression the temperature of a gas rises. (We shall see the atomic reason tor that later; for now, and throughout this chapter, we are keeping to the world of appearances and not delving into mechanisms.) The rise in temperature of the gas amplifies the rise in pressure that results from the confinement itself (because pressure increases with temperature); so, during an adiabatic compression, the pressure of a gas rises more sharply than during an isothermal compression (as is also illustrated above).

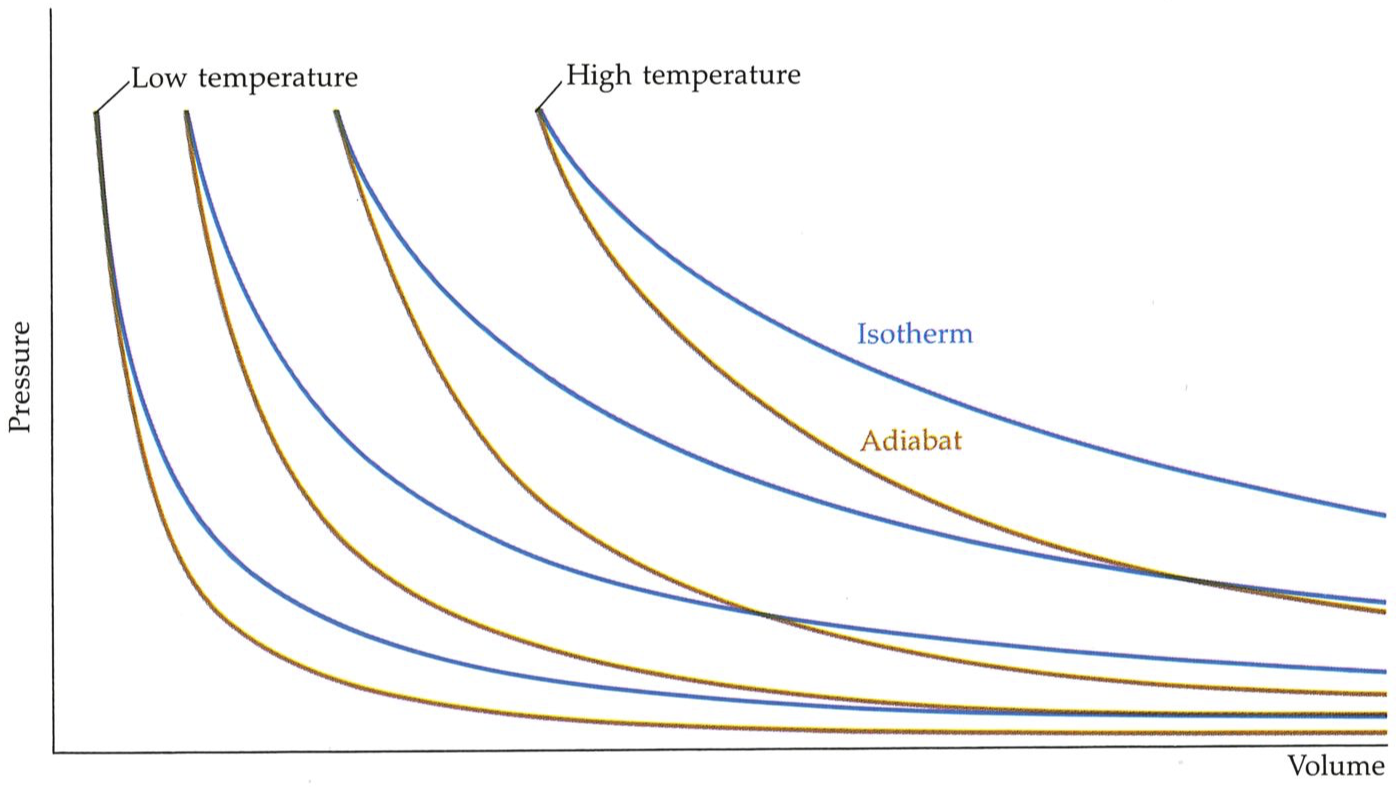
The relation between the pressure and the volume of a gas depends on the conditions under which the expansion or compression takes place. It the temperature is held constant, the relation is expressed by Boyle’s law that the pressure is inversely proportional to the volume: this gives res to the isotherms in the illustration. On the other hand, if the sample is thermally isolated. its temperature rises as it is compressed (and falls as it expands), and the dependence is as show by the adiabats.

The increasing pressure of a gas as its volume is reduced isothermally, and the even sharper increase when the compression is adiabatic, are reversed when the gas expands. If the expansion is isothermal, then the pressure drops as the volume increases; if the expansion is adiabatic, then the pressure falls more sharply because the gas also cools. This is also shown in the figure above, which therefore summarizes most of the essential features of a gas.

The four steps of the Carnot cycle are illustrated at the top of the next page, and the behavior of the pressure of the confined gas is illustrated in the indicator diagram at the bottom of the next page. The horizontal axis in the latter represents the location of the piston, but because the cylinder is uniform it also represents the volume available to the gas; so from now on we shall interpret it as the volume.

The initial state of the engine is represented by $A$ (in both illustrations). The hot source is in contact with the cylinder; so the gas is at the same temperature. The piston is in as far as it will go; so the volume is small. As a result of the high temperature and the confined volume, the pressure of the gas is high.

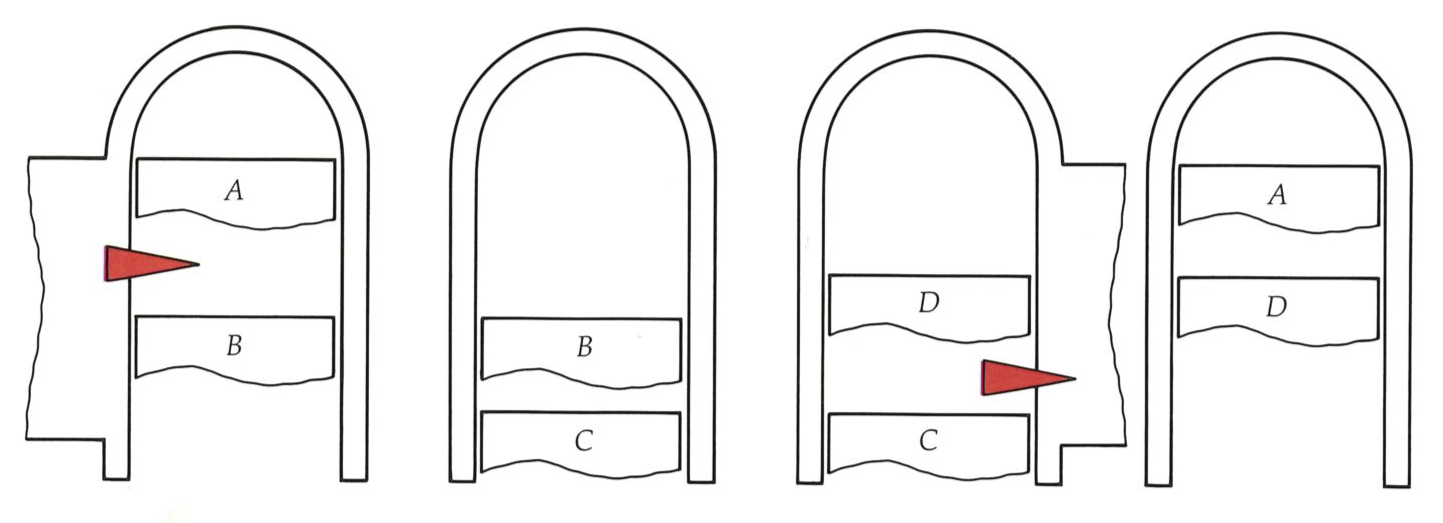
The Carnot cycle consists of four stages: A to $\mathrm{B}$ is an isothermal expansion; B to C is an adiabatic expansion. Both steps produce work. C to D is an isothermal compression; D to A is an adiabatic compression. These two steps consume work. Each stage is traversed quasistatically.

The first stage of the cycle is the expansion of the gas while the cylinder remains in contact with the hot source. The high-pressure gas pushes back the piston, and so the crank rotates. This is a power stroke of the engine. This step is isothermal (all at the same temperature); so, in order to overcome the tendency of the gas to cool as it expands, energy must flood in from the hot source. Therefore, not only is this the power stroke of the engine, it is also the step that sucks in energy-absorbs heat-from the hot source.

The designer of this engine could allow the crankshaft to continue to rotate, and so to return the piston to its initial position. Then, if the compression is also isothermal, the gas will be restored to its initial state. This would certainly fulfil one criterion: the cycle would be complete, the gas restored to its initial state, and the engine ready to go on again. We shall call this the Atkins cycle. Such a cycle is plainly useless, for in order to push the piston back to its starting position, exactly the same work needs to be done by the external, initially hopeful, but now disappointed user as had been obtained from the engine in the power stroke! This is illustrated in the figure below, where the rotating crankshaft takes the state of the gas from $A$ to $B$ and back to $A$ for ever, which is admirable, but the work generated in the first stage is reabsorbed in the second, which is not. Note, incidentally, that the area enclosed by the two lines that represent the useless Atkins cycle is zero: it is a standard result of elementary thermodynamics that the overall work produced during a complete cycle is given by the area it bounds on an indicator diagram. Here there is zero area between the two coincident curves: so zero work is produced overall.

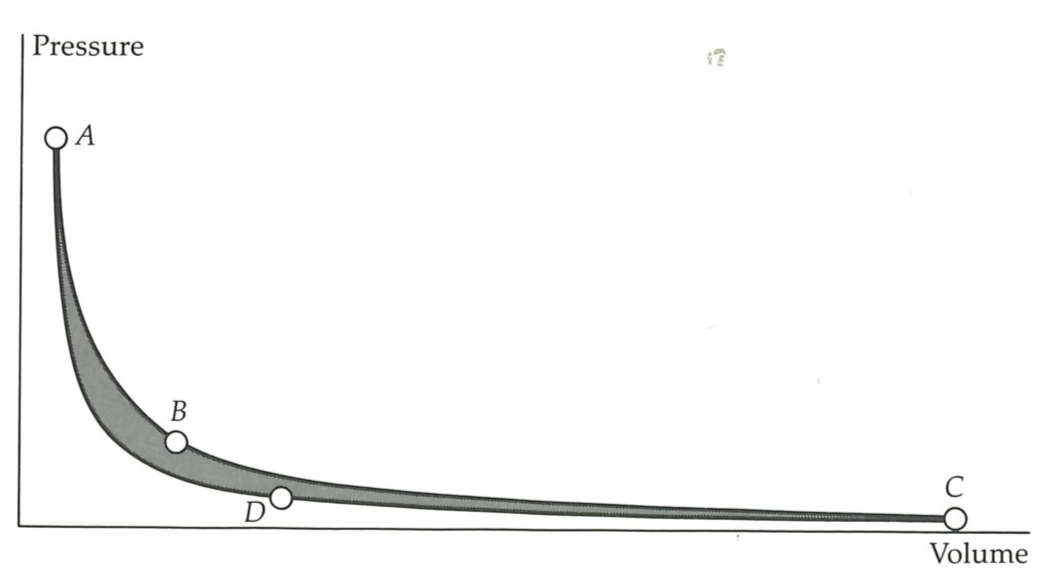
The indicator diagram for the Carnot cycle. $\mathrm{AB}$ and $\mathrm{CD}$ are isotherms (from the figure on page 17), and $\mathrm{BC}$ and $\mathrm{DA}$ are adiabats (from the same illustration). The work produced during the cycle is proportional to the shaded area.

In order to make the cycle useful, we have to arrange matters so that not all the work of the power stroke is lost in restoring the gas to its initial pressure, temperature, and volume. We need a way to reduce the pressure of the gas inside the cylinder, so that during the compression stage less work has to be done to drive the piston back in. One way of reducing the pressure of a gas is to lower its temperature. That we can do by including in the cycle a stage of adiabatic expansion; we have seen that such an expansion lowers the temperature.

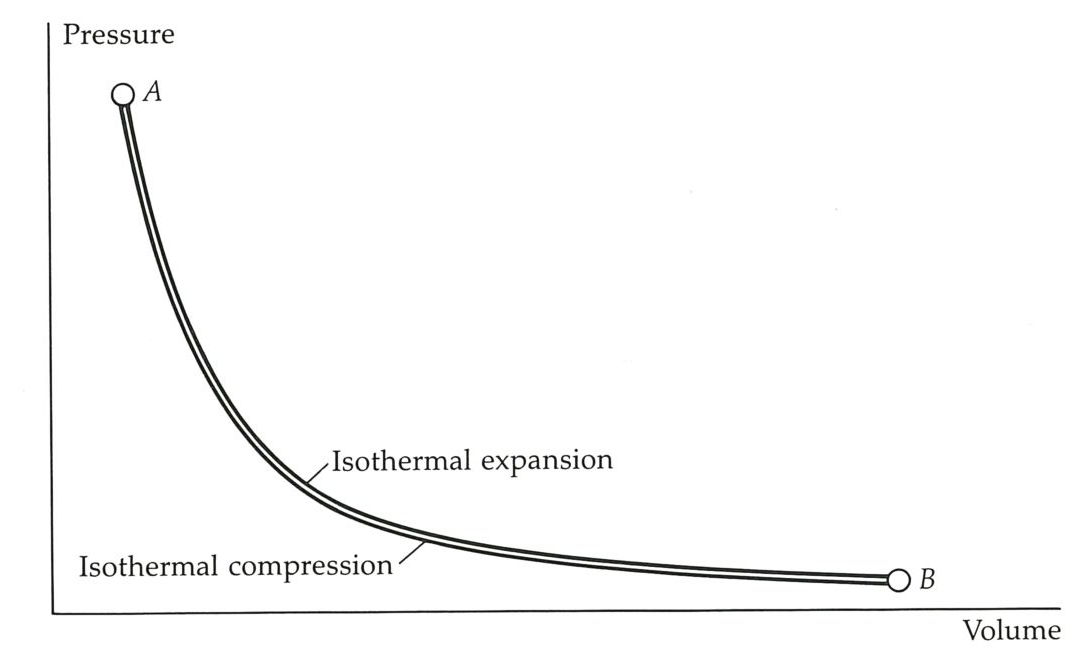
The indicator diagram for the Atkins cycle. The two steps are isothermal, and occur at the same temperature: the cycle is useless, because no work is produced overall.

The essential step in the Carnot cycle is therefore to break the thermal contact with the hot reservoir before the piston is fully withdrawn, at $B$ in the two figures opposite. The crank continues to turn, and the gas continues to expand. But now it does so adiabatically, and so both its pressure and its temperature fall. This takes its state to $C$. The stage from $B$ to $C$ is still a power stroke, but now we are cashing in the energy stored in the gas, for it can no longer draw on the supply from the hot source.

At this point we have to begin to restore the gas to its initial condition. The first restoration step involves pushing in the piston-doing workand reducing the volume toward its initial value. This stage (from $C$ to $D$ ) is performed with the gas in contact with the cold sink, to ensure that the pressure remains as low as possible and therefore that the work of compression is least. As the piston moves in, the gas tends to heat, but the thermal contact with the cold sink ensures that it remains at the same low temperature, for it can dump its extra energy into the sink.

This compression takes us to $D$. Now the volume of the confined gas is almost what it was initially, but its temperature is low. Therefore, before the crank has fully turned, we break the contact with the cold reservoir and allow the work of adiabatic compression to raise the temperature of the gas. If the timing is right, then the final surge of the piston not only compresses the gas to its initial volume, but also heats it to its initial temperature. The cycle is complete.*

• The Carnot cycle can be explored by using the first computer program listed in Appendix 3. The general definition of a Carnot cycle is any cycle in which there are two adiabatic and two isothermal stages.

Not only is the cycle complete, and the engine back exactly in its initial condition and ready to go through another, but work has been produced. As we set out to achieve, more work was produced in the power strokes than was absorbed in the restoration stages, because the compression work has been done against a lower pressure. This is reflected in the shape of the indicator diagram at the bottom of page 18: it now encloses nonzero area, and the work done by the engine overall is also nonzero.

But there is an exceedingly important point. Notice the importance of the cold sink. Without the cold sink we have the primitive and useless Atkins cycle, a sequence that is cyclic but workless. As soon as we allow energy to be discarded into a cold sink, the lower line of the indicator diagram drops away from the upper, and the area that the cycle encloses becomes nonzero: the sequence is still cyclic, but now it is useful. However, the price we have to pay in order to generate work from the heat absorbed from the hot source is to throw some of that heat away. This captures the essence of Carnot’s view that a heat engine is an energy mill (although we have discarded the conservation of caloric): energy drops from the hot source to the cold sink, and is conserved; but because we have set up this flow from hot to cold, we are able to draw only some energy off as work; so not all the energy drops into the cold. The cold sink appears to be essential, for only if it is available can we set up the energy fall, and draw off some as work.

Now we generalize. The Carnot cycle is only one way to extract work from heat. Nevertheless, it is the experience of everyone who has studied engines that, as in the Carnot cycle, in every engine there has to be a cold sink, and that at some stage of the cycle energy must be discarded into it. That little mouse of experience is nothing other than the Second Law of thermodynamics.

Thus the Second Law moves onto the stage. I have allowed it to creep in, because that emphasizes the extraordinary nature of thermodynamics. All the law seems to be saying is that heat cannot be completely converted into work in a cyclic engine: some has to be discarded into a cold sink. That is, we appear to have identified a fundamental tax: Nature accepts the equivalence of heat and work, but demands a contribution whenever heat is converted into work.

Note the dissymmetry. Nature does not tax the conversion of work into heat: we may fritter away our hard-won work by friction, and do so completely. It is only heat that cannot be so converted. Heat is taxed; not work.

The web of events is beginning to form. Bouncing balls come to rest; hot objects cool; and now we have recognized a dissymmetry between heat and work. The domain of the Second Law must now begin to spread outward from the steam engine and to claim its own. By the end of the book, we shall see that it will have claimed life itself.

---

---

2 THE SIGNPOST OF CHANGE

This is where we begin to define and refine corruption. So far we have seen that the immediate successors of Carnot were able to disentangle a rule about the quantity of energy from a rule about the direction of its conversion. Energy displaced heat as the eternally conserved; heat and work, hitherto regarded as equivalent, were shown to be dissymmetric. But these are bald, imprecise, and incomplete remarks: we must now sharpen them and put ourselves in a position to explore their ramifications. This we shall do in two stages. First, briefly, we shall refine the notions of heat and work, which so far we have regarded as “obvious” quantities. Then, with the precision such refinement will bring to the discussion, we shall start our main business, the refinement of the statement of the Second Law. With that refinement will come power and, as often happens, corruption too. We shall see that the domain of the Second Law is corruption and decay, and we shall see what extraordinarily wonderful things take place when quality gives way to chaos.

The Nature of Heat and Work

Central to our discussion so far, and for the next couple of chapters, are the concepts of heat and work. Perhaps the most important contribution of nineteenth-century thermodynamics to our comprehension of their nature has been the discovery that they are names of methods, not names of things. The early nineteenth-century view was that heat was a thing, the imponderable fluid “caloric”; but now we know that there is no such “thing” as heat. You cannot isolate heat in a bottle or pour it from one block of metal to another. The same is true of work: that too is not a thing; it can be neither stored nor poured.

Both heat and work are terms relating to the transfer of energy. To heat an object means to transfer energy to it in a special way (making use of a temperature difference between the hot and the heated). To cool an object is the negative of heating it: energy is transferred out of the object under the influence of a difference in temperature between the cold and the cooled. It is most important to realize, and to remember throughout the following pages (and maybe beyond), that heat is not a form of energy: it is the name of a method for transferring energy.

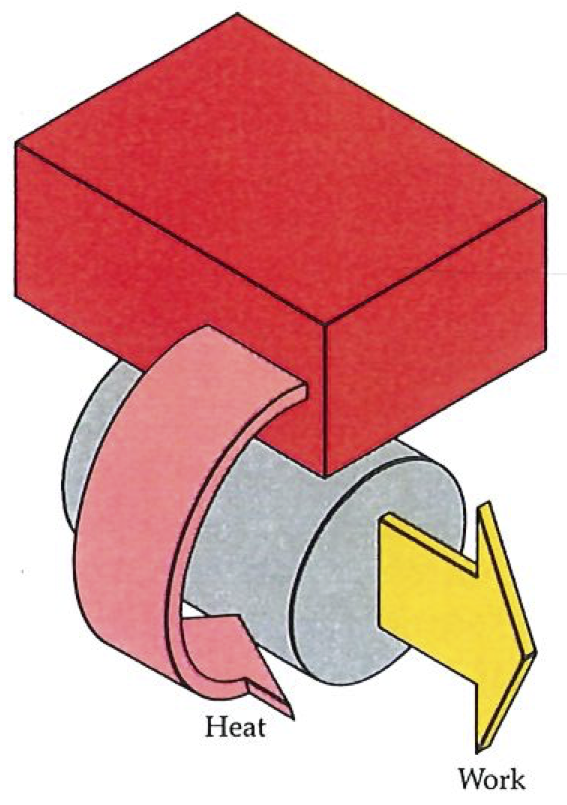
The Kelvin statement of the Second Law denies the possibility of converting a given quantity of heat completely into work without other changes occurring elsewhere.

The same is true of work. Work is what you do when you need to change the energy of an object by a means that does not involve a temperature difference. Thus, lifting a weight from the floor and moving a truck to the top of a hill involve work. Like heat, work is not a form of energy: it is the name of a method for transferring energy.

All that having been established, we are going to return to informality again. In chapter 1 we said things like “heat was converted into work”. If we were to speak precisely, we would have to say “energy was transferred from a source by heating and then transferred by doing work.” But such precision would sink this account under a mass of verbiage; so we shall use the natural English way of talking about heat and work, and use expressions such as “heat flows into the system…” But whenever we do, we shall always add in a whisper, “but we know what we really mean”.

The Seeds of Change

Now we refine the Second Law into a constructive tool. So far it has crept mouselike into the discussion as a not particularly impressive commentary on some not particularly interesting experience with engines. Cold sinks, we have seen, are necessary when we seek to convert heat into work. The formal restatement of this item of experience is known as the Kelvin statement of the Second Law:

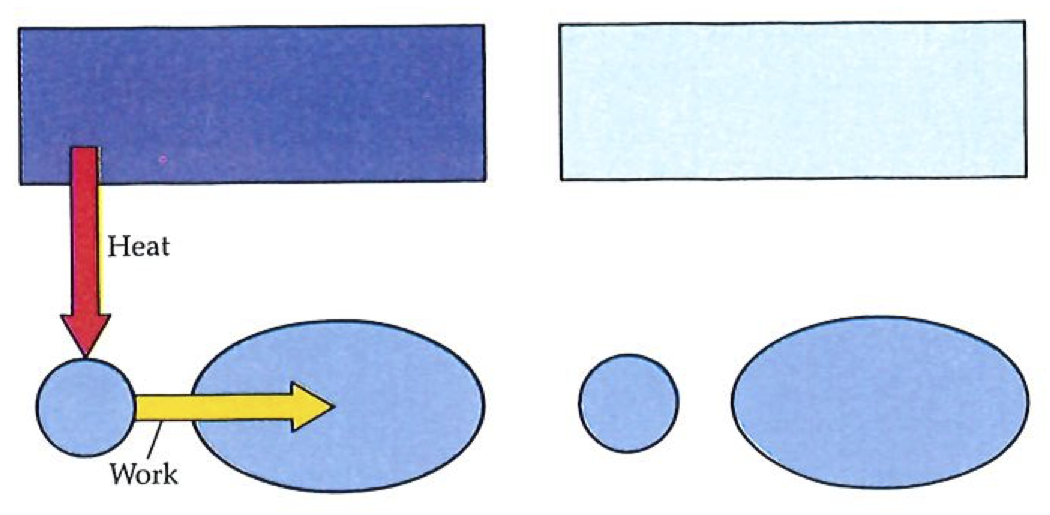
Second Law: No process is possible in which the sole result is the absorption of heat from a reservoir and its complete conversion into work.

The most important point to pick out of this statement of the Second Law is the dissymmetry of Nature that we have already mentioned. It states that it is impossible to convert heat completely into work (see figure up, on left); it says nothing about the complete conversion of work into heat. Indeed, as far as we know, there is no constraint on the latter process: work may be completely converted into heat without there being any other discernable change. For example, frictional effects may dissipate the work being done by an engine, as when a brake is applied to a wheel. All the energy being transferred into the outside world by the engine may be dissipated in this way. Here, then, is Nature’s fundamental dissymmetry; for although work and heat are equivalent in the sense that each is a manner of transferring energy, they are not equivalent in the manner in which they may interchange. We shall see that the world of events is the manifestation of the dissymmetry expressed by the Second Law.

The Kelvin statement should not be construed too broadly. It denies the existence of processes in which heat is extracted from a source, and converted completely into work, there being no other change in the Universe. It does not deny that heat can be completely converted into work when other changes are allowed to take place too. Thus cannons can fire cannonballs: the heat generated by the combustion of the charge is turned completely into the work of lifting the ball; however, cannons are literally one-shot processes, and the state of the system is quite different after the conversion (for instance, the volume of the gas that propelled the ball from the cannon remains large, and is not recompressed; cannons are not cycles).

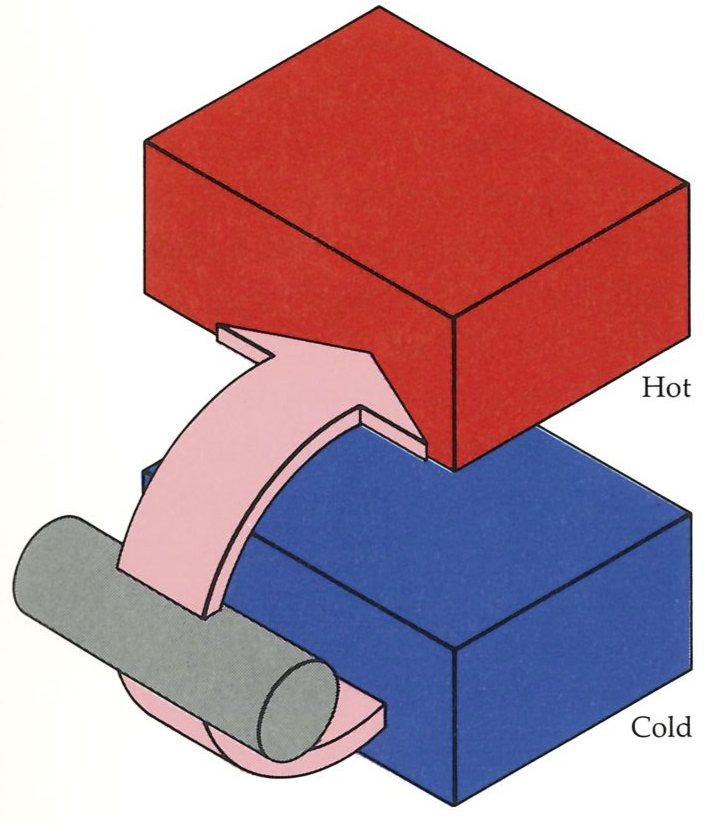
The Clausius statement of the Second Law denies the possibility of heat flowing spontaneously from a cold body to one that is hotter.

One delight of thermodynamics is the way in which quite unrelated remarks turn out to be equivalent. This is the way the subject creeps over the landscape of events and digests them. Now the mouse can begin to grow and claim its own.

As an example of this process of incorporation, which allows the Second Law to spread away from the steam engine, we shall set in apparent opposition to the Kelvin statement of the Second Law the rival formulation devised by Clausius:

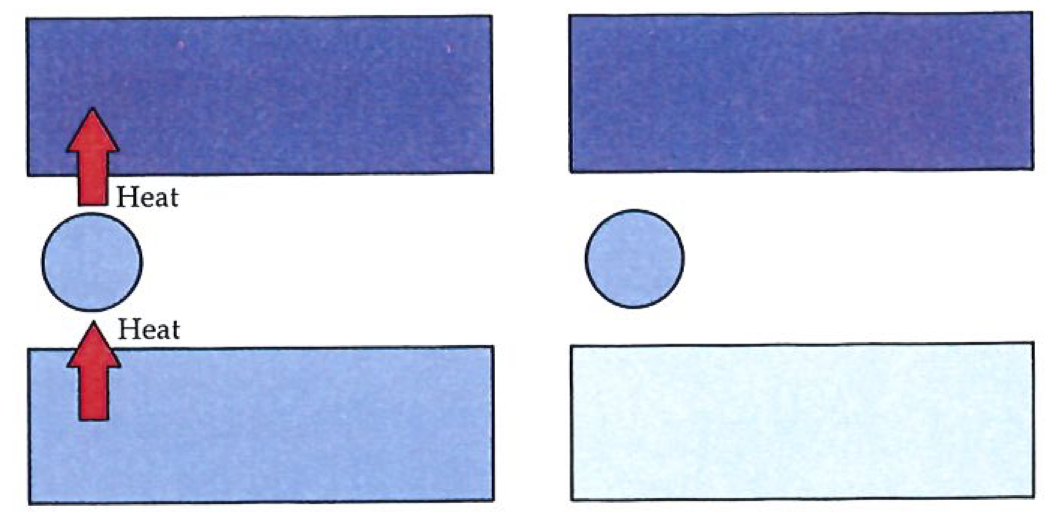
Second Law: No process is possible in which the sole result is the transfer of energy from a cooler to a hotter body.

First, note that the Clausius statement can stand on its own as a summary of experience: so far as we know, no one has ever observed energy to transfer spontaneously (that is, without external intervention) from a cool body to a hot body (see figure on left). The laws of thermodynamics ignore, of course, the sporadic reports of purported miracles, and its proven predictive power is a retrospective argument against their occurrence. The fact that we need to construct elaborate devices to bring about refrigeration and air conditioning, and must run them by using electric power, is a practical manifestation of the validity of the Clausius statement of the Second Law: for although heat will not spontaneously flow to a hotter body, we can cause it flow in an unnatural direction if we allow changes to take place elsewhere in the Universe. In particular, a refrigerator operates at the expense of a burning lump of coal, a stream of falling water, or an exploding nucleus elsewhere. The Second Law specifies the unnatural, but does not forbid us to bring about the unnatural by means of a natural change elsewhere.

Second, the Clausius statement, like the Kelvin statement, identifies a fundamental dissymmetry of Nature, but ostensibly a different dissymmetry. In the Kelvin statement the dissymmetry is that between work and heat; in the Clausius statement there is no overt mention of work. The Clausius statement implies a dissymmetry in the direction of natural change: energy may flow spontaneously down the slope of temperature, not up. The twin dissymmetries are the anvils on which we shall forge the description of all natural change.

But there cannot be two Second Laws of thermodynamics: if the twin dissymmetries of Nature are both to survive, they must be the outcome of a single Second Law or at least one that should be expressed more richly than either the Kelvin or the Clausius statement alone. In fact, the two statements, although apparently different, are logically equivalent: there is indeed only one Second Law, and it may be expressed as either statement alone. The twin dissymmetries, and the anvils, are really one.

In order to show that the two statements are equivalent, we use the logical device of demonstrating that the Kelvin statement implies the Clausius statement, and that the Clausius statement implies the Kelvin. Actually, in the slippery way that logicians have, what we shall do is exactly the opposite: we shall show that if we can disprove the Kelvin statement, then the falsity of the Clausius statement is implied, and if we can disprove the Clausius, then farewell Kelvin too. If the death of either one implies the death of the other, then the statements are equivalent.

For our purposes, we bring on the family Rogue: Jack Rogue, the purveyor of anti-Kelvin devices, and Jill Rogue, whose line consists of antiClausius devices. First Jack will present his wares.

We take Jack’s device, which he claims is an engine that contravenes Kelvin’s experience, and can convert heat entirely into work and produce no change elsewhere, and we connect it between a hot source and a cold sink (see figure on facing page). We also connect it to another (conventional) engine, which will be run as a refrigerator and used to pump energy from the same cold sink to the same hot source. According to Jack, all the heat drawn from the hot source is converted into work. Suppose, then, that we run the engine long enough to remove 100 joules of energy${}^{\ast }$ as heat, in which case, according to Jack, 100 joules of work are produced by his excellent machine. If that is so, then our other engine uses that 100 joules, and with it can transfer some energy from the cold sink to the hot source; the total energy it dumps as heat into that source is the sum of Jack’s engine supplies. This must be so in the 100 joules of energy that Law (which both Jack and Jill accept). These in order to accord with the First in the figure on the facing page. The overall effect, therefore, is to transfer heat from cold to hot, there being no other change. Thus Jack’s device pleases Jill.

• The units for expressing quantities of energy, whether they are simply stored or are being shipped as heat or as work, are explained in Appendix 1 . We shall use joules.

The argument to show that a failure of the Kelvin statement implies a failure of the Clausius statement involoes connecting an ordinary engine between two reservoirs and driving it with an anti-Kelvin device. The net effect of the flows of energy shown here is to transport heat spontaneously from the cold to the hot reservoir, contradicting Clausius.

Happy Jill now shows her device, which, she claims, spontaneously pumps heat from a cold sink to a hot source and leaves no change elsewhere. As was done with Jack’s, Jill’s device is connected between a hot source and a cold sink, and another engine is also connected between the two (see figure on next page). Jill runs her device, which pumps 100 joules of energy from cold to hot, and does so without any interference from outside, thus denying Clausius’s experience of life. The other engine is arranged to run, and to dump 100 joules of energy into the cold sink, providing the balance of whatever it draws from the hot source as work.

Toward Corruption

The progress of science is marked by the transformation of the qualitative into the quantitative. In this way not only do notions become turned into theories and lay themselves open to precise investigation, but the logical development of the notion becomes, in a sense, automated. Once a notion has been assembled mathematically, then its implications can be teased out in a rational, systematic way. Now, we have promised that this account of the Second Law will be non mathematical, but that does not mean we cannot introduce a quantitative concept. Indeed, we have already met several, temperature and energy among them. Now is the time to do the same thing for spontaneity.

The idea behind the next move can be described as follows. The Zeroth Law of thermodynamics refers to the thermal equilibrium between objects (“objects”, the things at the center of our attention, are normally referred to as systems in thermodynamics, and we shall use that term from now on). Thermal equilibrium exists when system $A$ is put in thermal contact with system $B$, but no net flow of energy occurs. In order to express this condition, we need to introduce the idea of the temperature of a system, which we define as meaning that if $A$ and $B$ happen to have the same temperature, then we know without further ado that they are in thermal equilibrium with each other. That is, the Zeroth Law gives us a reason to introduce a “new” property of a system, so that we can easily decide whether or not that system would be in thermal equilibrium with any other system if they were in contact.

The First Law gives us a reason to carry out a similar procedure, but now one that leads to the idea of “energy”. We may be interested in what states a system can reach if we heat it or do work on it. We can assess whether a particular state is accessible from the starting condition by introducing the concept of energy. If the new state differs in energy from the initial state by an amount that is different from the quantity of work or heating that we are doing, then we know at once, from the First Law, that that state cannot be reached: we have to do more or less work, or more or less heating, in order to bring the energy up to the appropriate value. The energy of a system is therefore a property we can use for deciding whether a particular state is accessible.

This suggests that there may be a property of systems that could be introduced to accommodate what the Second Law is telling us. Such a property would tell us, essentially at a glance, not whether one state of the system is accessible from the other (that is the job of the energy acting through the First Law), but whether it is spontaneously accessible. That is, there ought to be a property that can act as the signpost of natural, spontaneous change, change that may occur without the need for our technology to intrude into the system in order to drive it.

An isolated system may in principle change its state to any other of the same energy (the four colored boxes in the horizontal row), but the First Law forbids it to change to states of different energy (the brown-tinted boxes).

There is such a property. It is the entropy of the system, perhaps the most famous and awe-inspiring thermodynamic property of all. Awe-inspiring it may be: but the awe should not be misplaced. The awe for entropy should be reserved for its power, not for its difficulty. The fact that in everyday discourse “entropy” is a word far less common than “energy” admittedly makes it less familiar, but that does not mean that it stands for a more difficult concept. In fact, I shall argue (and in the next chapter hope to demonstrate) that the entropy of a system is a simpler property to grasp than its energy! The exposure of the simplicity of entropy, however, has to await our encounter with atoms. Entropy is difficult only when we remain on the surface of appearances, as we do now.

Entropy

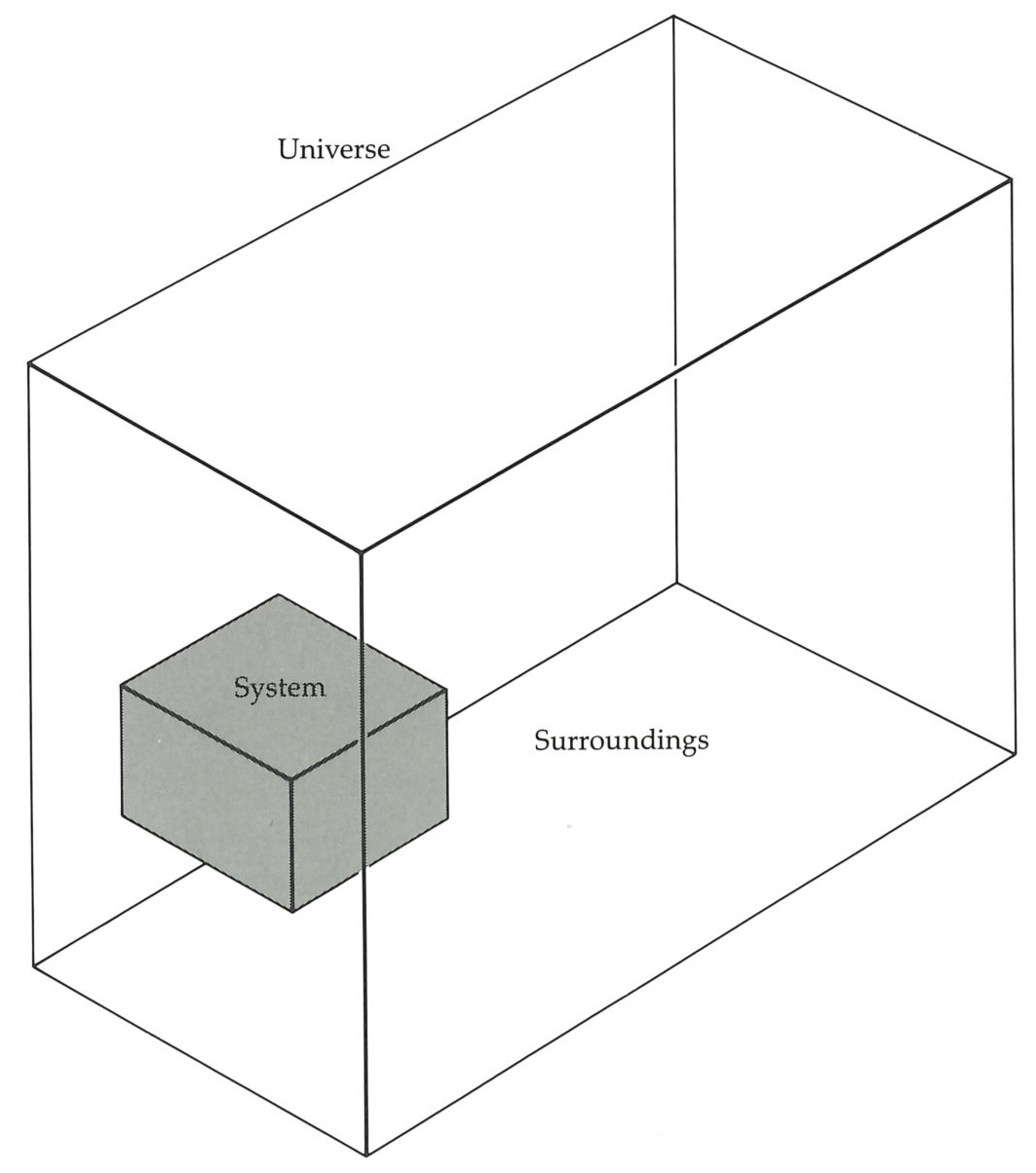
We are now going to build a working definition of entropy, using the information we already have at our disposal. The First Law instructs us to think about the energy of a system that is free from all external influences; that is, the constancy of energy refers to the energy of an isolated system, a system into which we cannot penetrate with heat or with work, and which for brevity we shall refer to as the universe (see figure on facing page). Similarly, the entropy we define will also refer to an isolated system, which we shall call the universe. Such names reflect the hubris of thermodynamics: later we shall see to what extent the “universe” is truly the Universe.

In thermodynamics we focus attention on a region called the system. Around it are the surroundings. Together the two constitute the universe. In practice, the universe may be only a tiny fragment of the Universe itself, such as the interior of a thermally insulated, closed container, or a water bath maintained at constant temperature.

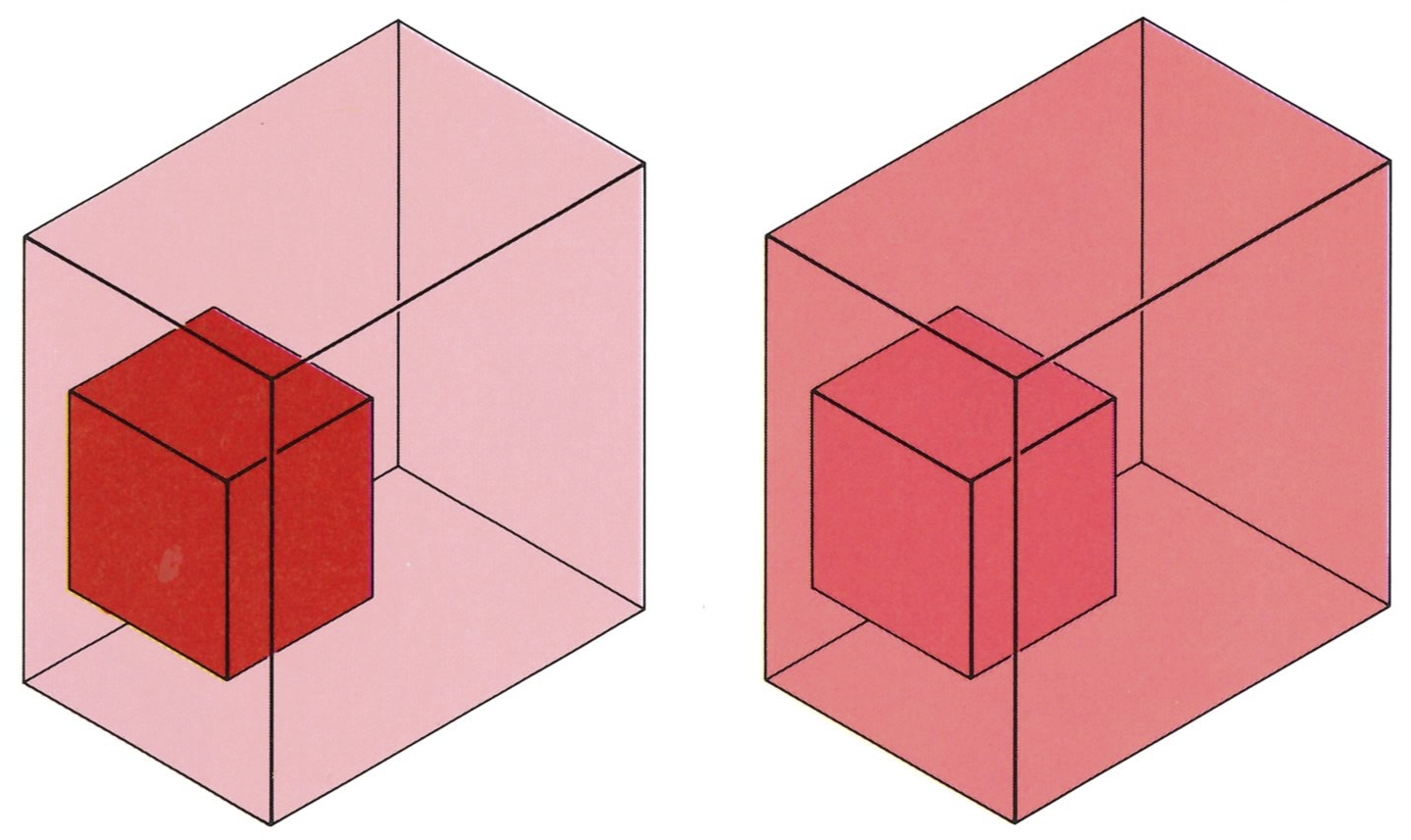
Suppose there are two states of the universe; for instance, in one a block of metal is hot, and in the other it is cold (see top figure on next page). Then the First Law tells us that the second state can be reached from the first only if the total energy of the universe is the same for each. The Second Law examines not the label specifying the energy of the universe, but another label that specifies the entropy. We shall define the entropy so that if it is greater in state $B$ than in state $A$, then state $B$ may be reached spontaneously from state $A$ (see lower figure on next page). On the other hand, even though the energy of states $A$ and $B$ may be the same, if the entropy of state $B$ is less than the entropy of state $A$, then state $B$ cannot be reached spontaneously: in order to attain it, we would have to unzip the insulation of the universe, reach in with some technology (such as a refrigerator), and drive the universe from state $A$ to state $B$ (at the expense of a change in our larger Universe).

We have to construct a definition of entropy in such a way that in any universe entropy increases for natural changes, and decreases for changes that are unnatural and have to be contrived.

An isolated system (a universe) containing a hot block of metal is in a different state from one containing a similar but cold block, even if the total energy is the same in each. There must be a property other than total energy that deter mines the direction of spontaneous change will be hot $⟶$ cold rather than the reverse…

Furthermore, we want to define it so that we capture the Clausius and Kelvin statements of the Second Law, and arrive at a way of expressing them both simultaneously in the following single statement:

Second Law: Natural processes are accompanied by an increase in the entropy of the universe.

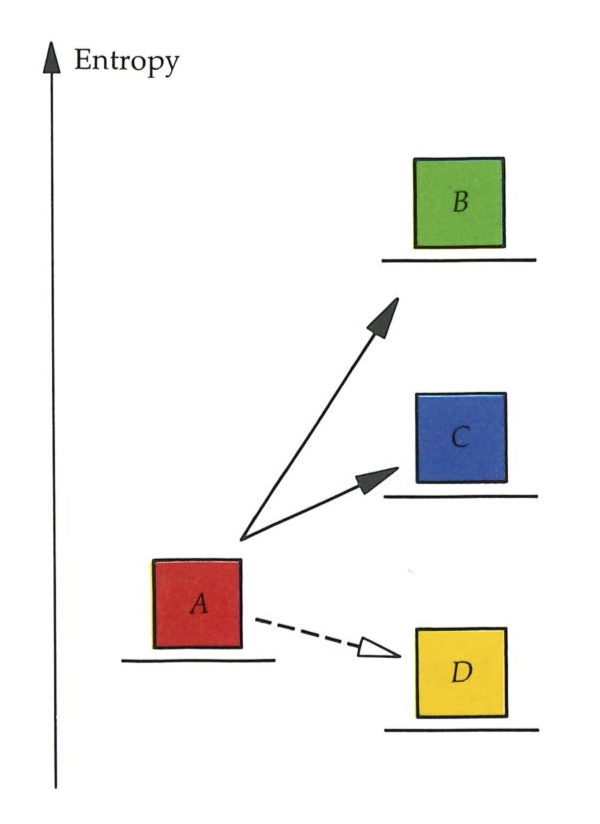
The states $\mathrm{A},\mathrm{B},\mathrm{C}$, and $\mathrm{D}$ in the illustration on page 30 have the same energy, but different entropies. The changes $\mathrm{A}$ to $\mathrm{B}$ and $\mathrm{A}$ to $\mathrm{C}$ may occur spontaneously, because each involves an increase of entropy; the change from $A$ to $D$ does not occur spontaneously, because it would require the entropy of the universe to drop. The universe always falls upward in entropy.

This is sometimes referred to not as the Second Law (which is properly a report on direct experience), but as the entropy principle, for it depends on a specification of the property “entropy,” which is not a part of direct experience. (Similarly, the statement “energy is conserved” is also more correctly referred to as the energy principle, for the First Law itself is also a commentary on direct experience of the changes that work can bring about, whereas the more succinct statement depends on a specification of what is meant by “energy.”)

The Kelvin statement is reproduced by the entropy principle if we define the entropy of a system in such a way that entropy increases when the system is heated, but remains the same when work is done. By implication, when a system is cooled its entropy decreases. Then Jack’s engine is discounted by the Second Law, because heat is taken from a hot source (so that its entropy declines), and work is done on the surroundings (with the result that the entropy of the surroundings remains the same), as shown in the top figure on the facing page, and so overall the entropy of the little engine is that contains his engine and its surroundings decreases; hence his engine is unnatural.

The shades of blue denote the entropies of the stored energy. When heat is withdrawn by the anti-Kelvin device, the entropy of the hot reserooir falls, but the quasistatic work does not producc entropy elsewhere. Overall, therefore, the cutropy of the universe declines, which is against experience.

In order for us to discount Jill’s device, the definition of entropy must depend on the temperature. We can capture her (and Clausius) if we suppose that the higher the temperature at which heat enters a system, the smaller the resulting change of entropy. In her anti-Clausius device, heat leaves the cold system, and the same quantity is dumped into the hot. Since the temperature of the cold reservoir is lower than that of the hot, the reduction of its entropy (see below) is greater than the increase of the entropy of the hot reservoir; so overall Jill’s device reduces the entropy of the universe, and it is therefore unnatural.

Now the net is beginning to close in on natural change. We have succeeded in capturing Jack and Jill jointly on a single hook, just as we have claimed that the entropy principle captures the two statements of the Second Law. From now on we should be able to discuss all natural change in terms of the entropy.

As in the illustration above, the shade of blue denotes the entropy. When heat is withdrawn from the cold reservoir, its entropy drops; when the same quantity of heat enters the hot reservoir, its entropy barely changes. Overall, therefore, the entropy of the universe declines, which is also against experience.

Yet we are still hovering on the brink of actually defining entropy! Now is the time to take the plunge. We have seen that entropy increases when a system is heated; we have seen that the increase is greater the lower the temperature. The simplest definition would therefore appear to be:

$$\mathit{\text{Change in entropy }}=\mathit{\text{( Heat supplied ) / Temperature}}$$

Happily, with care, this definition works.

First, let us make sure this definition captures what we have already done. If energy is supplied by heating a system, then Heat supplied is positive, and so the change of entropy is also positive (that is, the entropy increases). Conversely, if the energy leaks away as heat to the surroundings, Heat supplied is negative, and so the entropy decreases. If energy is supplied as work and not as heat, then Heat supplied is zero, and the entropy remains the same. If the heating takes place at high temperature, then Temperature has a large value; so for a given amount of heating, the change of entropy is small. If the heating takes place at low temperatures, then Temperature has a small value; so for the same amount of heating, the change of entropy is large. All this is exactly what we want.

Now for the care in the use of the definition. The temperature must be constant throughout the transfer of the energy as heat (otherwise the formula would be meaningless). Generally a system gets hotter (that is, its temperature will rise) as heating proceeds. However, if the system is extremely large (for example, if it is connected to all the rest of the actual Universe), then however much heat flows in, its temperature remains the same. Such a component of the universe is called a thermal reservoir. Therefore we can safely use the definition of the change of entropy only for a reservoir. That is the first limitation (it may seem extreme, but we shall A second point concerns the manner in a moment).

A second point concerns the manner in which energy is transferred. Suppose we allow an engine to do some work on its surroundings. Unless we are exceptionally careful, the raising of the weight, the turning of the crank, or whatever, will give rise to turbulence and vibration, which will fritter energy away by friction and in effect heat the surroundings. In that the change in entropy. In order to eliminate this from the definition (but once again only in order to clarify the definition, not to eliminate dissipative processes from the discussion), we must specify how the energy is to be transferred. The energy must be transferred without generating turbulence, vortices, and eddies. That is, it has to be done infinitely carefully: pistons must be allowed to emerge infinitely slowly, and energy must be allowed to seep down a temperature gradient infinitely slowly. Such processes are then called quasistatic: they are the limits of processes carried out with ever-increasing care.

Measuring the Entropy

We have a definition of entropy, but the definition does not seem to give the concept much body. Although we regard properties such as temperature and energy to be “tangible” (but we do so merely because they are familiar), the idea of entropy as $\mathit{\text{Change in entropy }}=\mathit{\text{( Heat supplied ) / Temperature}}$ seems remote from experience. So it is, and so it will remain until the next chapter, where we shall add flesh by considering how to interpret the concept in terms of the behavior of atoms.

But is temperature really so familiar, and entropy so remote? We think of a liter of hot water and a liter of cold water as having different temperatures. In fact, they also have different entropies, and the “hot” water has both a higher entropy and a higher temperature than the cold water. The fact that hot water added to cold results in tepid water is a consequence of the change of entropy. Should we think then of “hotness” as denoting high temperature or as denoting high entropy? With which concept are really familiar?

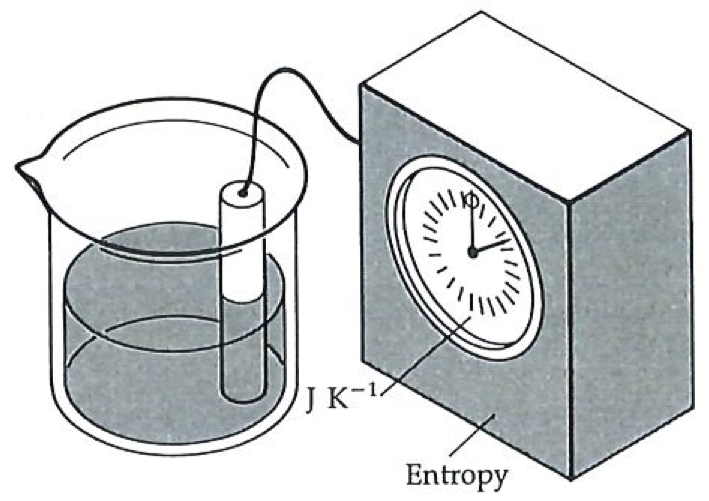
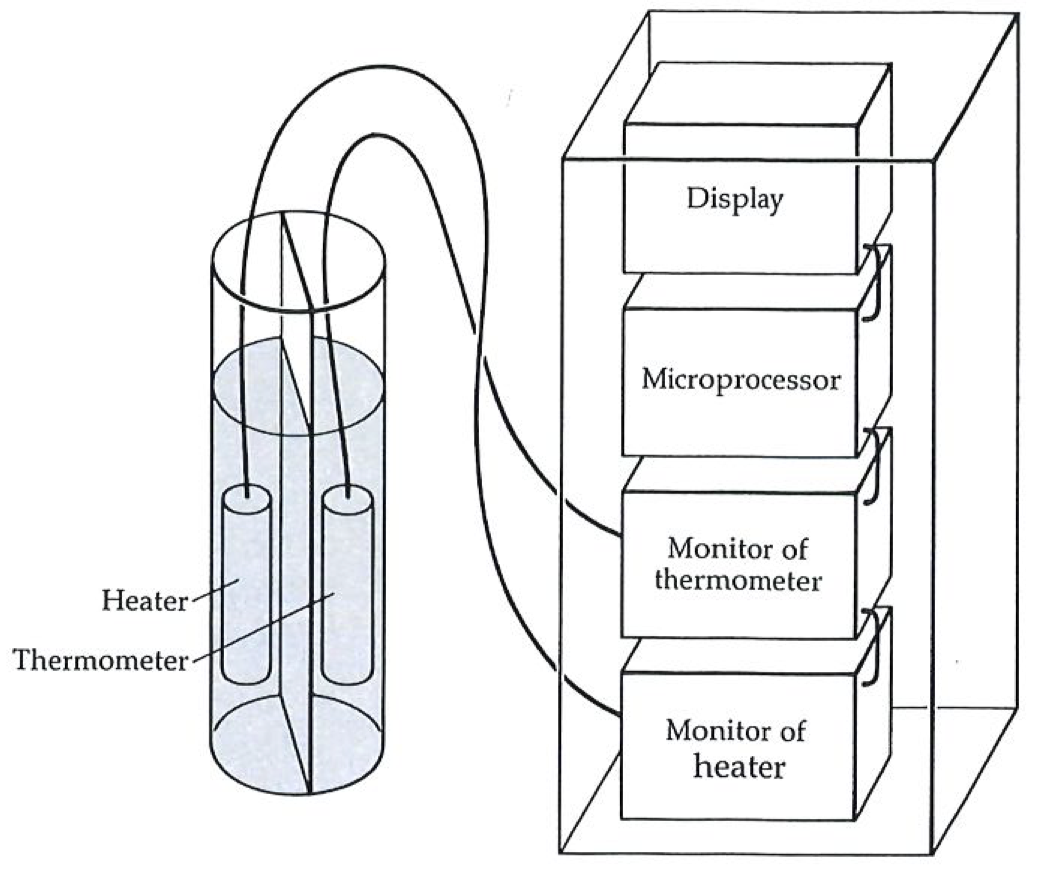
An entropy meter consists of a probe in the sample and a pointer giving a reading on a dial, exactly like a thermometer.

Temperature seems familiar because we can measure it: we feel at home with pointer readings, and often mistake the reading for the concept. Take time, for instance: the pointer readings are an everyday commonplace, but the essence of time is much deeper. So it is with temperature; although it seems familiar, the nature of temperature is a far more subtle concept. The difficulty with accepting entropy is that we are not familiar with instruments that measure it, and consequently we are not familiar with their pointer readings. The essence of entropy, when we get to it, is certainly no more difficult, and may be simpler, than the essence of temperature. What we need, therefore, in order to break down the barrier between us and entropy, is an entropy meter.

The figure to the left shows an entropy meter; the figure on the next page indicates the sort of mechanism that we might find inside it: it is basically a thermometer attached to a microprocessor. The readings can be taken from the digital display.

Suppose we want to measure the entropy change when a lump of iron is heated. All we need do is attach the entropy meter to the lump, and start heating: the microprocessor monitors the temperature indicated by the thermometer, and converts it directly into an entropy change. What calculations it does we shall come to in a moment. The care we have to exercise is to do the heating extremely slowly, so that we do not create hot spots and get a distorted reading: the heating must be quasistatic.

The interior of the entropy meter is more complicated than that of a simple mercury thermometer. The probe consists of a heater (whose output is monitored by the rest of the meter) and a thermometer (which is also monitored). The microprocessor is programmed to do a calculation based on how the temperature of the sample depends on the heat supplied by the heater. The output shown on the dial is the entropy change of the sample between the starting and finishing temperatures.

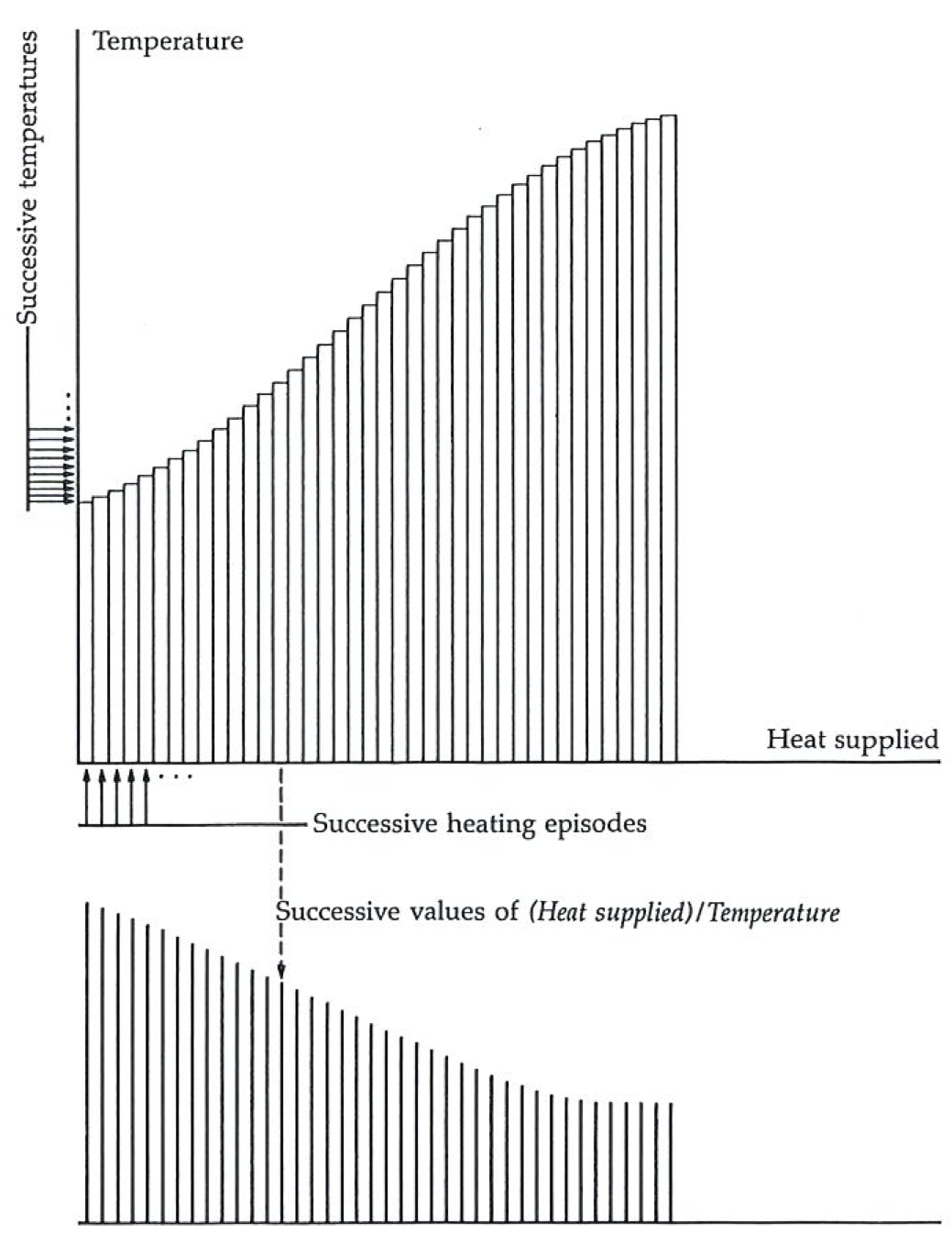
The microprocessor is programmed as follows. First, it has to work out, from the rise in temperature caused by the heating, the quantity of energy that has been transferred to the lump from the heater. That is a fairly straightforward calculation once we know the heat capacity (the specific heat) of the sample, because the temperature rise is directly proportional to the heat supplied:

$$\mathit{\text{Temperature rise }}=\mathit{\text{( Proportionality coefficient )}}\times \mathit{\text{(Heat supplied)}}$$

the coefficient being related to the heat capacity. (We could always measure the heat capacity in a separate experiment, with the same apparatus, but with a different program in the microprocessor.) The heater supplies only a trickle of energy to the sample, and the microprocessor evaluates $\mathit{\text{( Heat supplied ) / Temperature}}$, and stores the result. If only a little heat is supplied, the temperature will hardly rise, and so the entropy formula is very accurate. However, since the sample is not an infinite reservoir, the temperature does rise a little, and the next trickle of heat takes place at a slightly trickle of $\mathit{\text{( Heat supplied ) / Temperature}}$ at a marginally (in the limit, infinitesimally) higher temperature.

The procedure continues: the thermometer records, the microprocessor goes on dividing and adding, and the heating continues until at long last (in a perfect experiment, at the other end of eternity) the temperature has risen to the final value. The microprocessor then displays the accumulated sum of all the little values of $\mathit{\text{( Heat supplied ) / Temperature}}$ as the change in entropy of the lump.

The entropy meter works by squirting tiny quantities of heat into the sample, and monitoring the temperature. It then evaluates $\mathit{\text{( Heat supplied ) / Temperature}}$, and stores the result, Next it monitors the new temperature, and squirts in some more heat, and repeats the calculation. This is repeated until the final temperature has been reached. In a real-life measurement, the heat capacity of the sample is measured over the temperature range, and the entropy change is calculated from that (see Appendix 2).

That is as far as we need go for now. What I want to establish here is not so much the details of how the entropy change is measured in any particular process, but the fact that it is a measurable quantity, exactly like the temperature, and, indeed, that it can be measured with a thermometer too!

The Dissipation of Quality

We can edge closer to complete understanding by reflecting on the implications of what this external view of entropy already reveals about the nature of the world. As a first step, we shall see how the introduction of entropy leads to a particularly important interpretation of the role of energy in events.

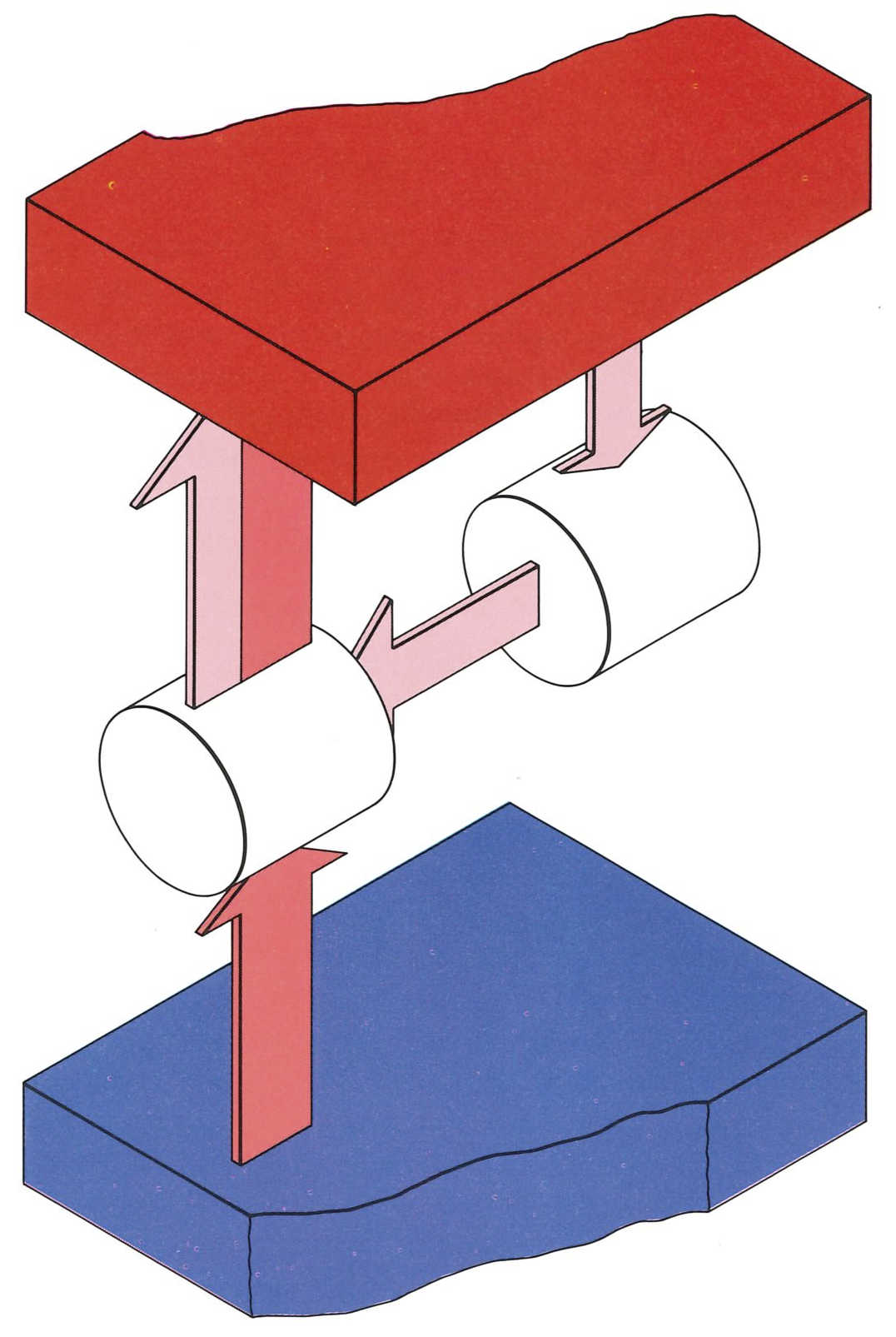
Suppose we have a certain amount of energy that we can draw from a hot source, and an engine to convert it into work. We know that the Second Law demands that we have a cold sink too; so we arrange for the engine to operate in the usual way. We can extract the appropriate quantity of work, and pay our tax to Nature by dumping a contribution of energy as heat into the cold sink. The energy we have dumped into the cold sink is then no longer available for doing work (unless we happen to have an even colder reservoir available). Therefore, in some sense, energy stored at a high temperature has better “quality”: high-quality energy is available for doing work; low-quality energy, corrupted energy, is less available for doing work.

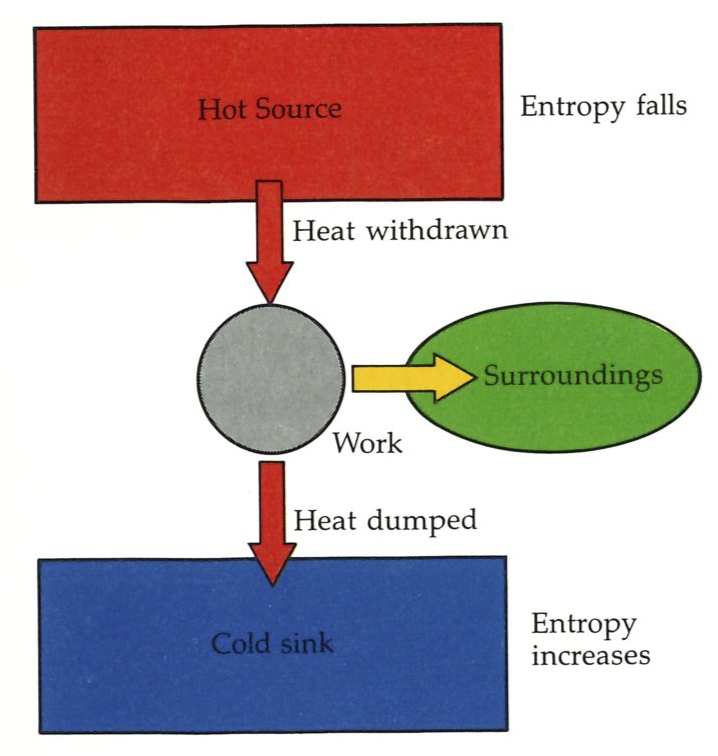
Some heat must be discarded into a cold sink in order for us to generate enough entropy to overcome the decline taking place in the hot reservoir.

A slightly different way of looking at the quality of energy is to think in terms of entropy. Suppose we withdraw a quantity of energy as heat from the hot source, and allow it to go directly to the cold sink (see the figure to the left). The entropy of the universe decreases by an amount $\mathit{\text{(Heat withdrawn)}}/T_{\text{HOT SOURCE}}$ but also increases by an amount $\mathit{\text{(Heat dumped)}}/T_{\text{COLD SINK}}$. The sum of the two contributions to the overall change in entropy is therefore positive (because the temperature of the hot source is higher than that of the cold sink). The energy of the universe is then less available for doing work (because when energy is stored at lower temperatures, still colder sinks are needed if it is to be converted into work). It is then, in our sense, lower in quality, and the entropy associated with the energy has increased. The entropy, therefore, labels the manner in which the energy is stored: if it is stored at a high temperature, then its entropy is relatively low, and its quality is high. On the other hand, if the same amount of energy is stored at a low temperature, then the entropy of that energy is high, and its quality is low.

Just as the increasing entropy of the universe is the signpost of natural change and corresponds to energy being stored at ever-lower temperatures, so we can say that the natural direction of change is the one that causes the quality of energy to decline: the natural processes of the world are manifestations of this corruption of quality.

This attitude toward energy and entropy, that entropy represents the manner in which energy is stored, is of great practical significance. The First Law establishes that the energy of a universe (and maybe of the Universe itself) is constant (perhaps constant at zero). Therefore, when we burn fossil fuels, such as coal, oil, and nuclei, we are not diminishing the supply of energy. In that sense, there can never be an energy crisis, for the energy of the world is forever the same. However, every time we burn a lump of coal or a drop of oil, and whenever a nucleus falls apart, we are increasing the entropy of the world (for all these are spontaneous processes). Put another way, every action diminishes the quality of the energy of the universe.

As technological society ever more vigorously burns its resources, so the entropy of the universe inexorably increases, and the quality of the energy it stores concomitantly declines. We are not in the midst of an energy crisis: we are on the threshold of an entropy crisis. Modern civilization is living off the corruption of the stores of energy in the Universe. What we need to do is not to conserve energy, for Nature does that automatically, but to husband its quality. In other words, we have to find ways of furthering and maintaining our civilization with a lower production of entropy: the conservation of quality is the essence of the problem and our duty toward the future.

Thermodynamics, particularly the Second Law (we shall see the less than benign role of the Third in a moment), indicates the problems in this program of conservation, and also points to solutions. In order to see how this is so, we shall go back to the Carnot cycle, and apply what we have developed here to its operation.

Ceilings to Efficiency

In the first place, if the Carnot engine goes through its cycle, then the entropy change of its little world cannot be negative, for that would signify a nonspontaneous process, and useful engines do not have to be driven. Now, however, we are equipped to calculate the change in entropy, using the formula $\mathit{\text{Heat}}/\mathit{\text{Temperature}}$. In order to calculate however, we must assume that the engine is working perfectly, and that there are no losses of any kind: the cycle must be gone round quasistatically.

The engine itself returns to its initial condition (it is cyclic); so at the end of a cycle it has the same entropy as it had at the beginning. The work it does in the surroundings does not increase their entropy, because everything happens so carefully and slowly in the quasistatic operating regime. The only changes of entropy are in the hot source, the entropy of which decreases by an amount of magnitude

$$\mathit{\text{(Heat supplied from hot source)}}/T_{\text{HOT SOURCE}}$$

and in the cold sink, the entropy of which increases by an amount of magnitude

$$\mathit{\text{(Heat supplied to cold sink)}}/T_{\text{COLD SINK}}$$

And, under quasistatic conditions, that is all. However, overall the change of entropy must not be negative. Therefore the smallest value of the heat discarded into the cold sink must be large enough to increase the entropy there just enough to overcome the decrease in entropy in the hot source. It is straightforward algebra to show that this minimum discarded energy is

$$\mathit{\text{(Minimum heat discard into the cold sink)}}=\mathit{\text{(Heat supplied by hot source)}}\times T_{\text{HOT SOURCE}}/T_{\text{HOT SOURCE}}$$

Here is our first major result of thermodynamics: we now know how to minimize the heat we throw away: we keep the cold sink as cold as possible, and the hot source as hot as possible. That is why modern power stations use superheated steam: cold sinks are hard to come by; so the most economical procedure is to use as hot a source as possible. That is, the designer aims to use the highest-quality energy.

But we can go on, and summon up our second major result. The work generated by the Carnot engine as it goes through its cycle must be equal to the difference between the heats supplied and discarded (this is a consequence of the First Law). The work is therefore equal to Heat supplied minus Heat discarded (see the preceding figure). We are now, however, in a position to express this difference in terms of the Heat supplied multiplied by a factor involving the two temperatures. The efficiency of the engine is the arrive at the result that the efficiency of a Carnot engine, working perfectly between a hot source and a cold sink, is between a hot source and a cold sink, is

$$\mathit{\text{Efficiency}}=1-T_{\text{HOT SOURCE}}/T_{\text{HOT SOURCE}}$$

That is, the efficiency depends only on the temperatures and is independent of the working material in the engine, which could be air, mercury, steam, or whatever. Most modern power plants for electricity generation use steam at around $1,{000}^{\circ }\mathrm{F}(800\mathrm{K})$ and cold sinks at around $212\mathrm{F}$ $(373\mathrm{K}){.}^{\ast }$ Their efficiency ceiling is therefore around 54 percent (but other losses reduce this efficiency to around 40 percent). Higher source temperatures could improve efficiencies, but bring other problems, because then materials begin to fail. For safety reasons, nuclear reactors operate at lower source temperatures (of about ${600}^{\circ }\mathrm{F},620\mathrm{K}$ ), which limits their theoretical efficiency to around 40 percent. Losses then reduce this figure to about 32 percent. Closer to home, an automobile engine operates with a brietly maintained input temperature of over 5,400 ${}^{\circ }\mathrm{F}$ (around 3,300 K) and erhausts at around $2,{100}^{\circ }\mathrm{F}(1,400\mathrm{K})$, giving a theoretical ceiling of around 56 percent. However, actual automobile engines are designed to be light enough to be responsive and mobile, and therefore attain only about 25 percent efficiency.

• Scales of temperature are described in Appendix 1. K denotes kelvin the graduation of the Kelvin scale of temperature (the one of fundamental significance in contrast to the contrived scales of Celsius and Fahrenheit). In brief, a temperature in kelvins is obtained by adding 273 to the temperature in degree Celsius.

The profound importance of the preceding result is that is puts an upper limit on the efficience of engines: whatever clever mechanism is contrived, so long as the engineer is stuck with fixed temperatures for the source and the sink, the efficiency of the engine cannot exceed the Carnot value. The reason why should by now be clear (to the external observer). In order for heat to be converted to work spontaneously, there must be an overall increase in the entropy of the universe. When energy is withdrawn as heat from the hot source, there is a reduction in its entropy. Therefore, since the perfectly operating engine does not itself generate entropy, there must be entropy generated elsewhere. Hence, in order for the engine to operate, there must be a dump for at least a little heat: there must be a sink. Moreover, that sink must be a cold one, so that even a small quantity of heat supplied to it results in a large increase in entropy.

The temperature of the cold sink amplifies the effect of dumping the heat: the lower the temperature, the higher the magnification of the entropy. Consequently, the lower the temperature, the less heat we need to discard into it in order to achieve an overall positive entropy change in the universe during the cycle. Hence the efficiency of the conversion increases as the temperature of the cold source is lowered.

There appears to be a limit to the lowness of temperature. The conversion efficiency of heat to work cannot exceed unity, for otherwise the First Law would be contravened. Therefore the value of $Tenperatur{e}_{\text{COLD SINK}}$ cannot be negative. Hence there appears to be a natural limit to the lowness of temperature, corresponding to Temperature $Tenperatur{e}_{\text{COLD SINK}}=0$. This is the absolute zero of temperature, the end of getting cold. At this infinite arctic, the conversion efficiency would be unity, for even the merest wisp of heat transferred to the sink would give an enormous positive entropy (because the temperature is in the denominator, so that $1/Temperature$ becomes infinitely large and magnifies everything infinitely). But can we attain that Nirvana?

A clue to the attainability of absolute zero can be obtained by considering the Carnot cycle with an ever-decreasing temperature of its cold sink. For a given quantity of heat to be absorbed from the hot source, the piston needs to travel out a definite distance from $A$ to $B$ in the figure on page 18 , no matter what becomes of the energy later. The cooling step, the adiabatic expansion from $C$ to $D$, then involves a greater expansion the lower the temperature we are aiming to reach. Some of the expansions are illustrated in the figure on the next page: we can see that the lower the temperature aimed at, the greater the size of the stroke. (This point can be explored by using the Carnot cycle program in Appendix 3.) In order to approach very low temperatures, we need extremely large engines. In order to reduce the temperature to zero, we would need an infinitely large engine. Absolute zero appears to be unattainable.

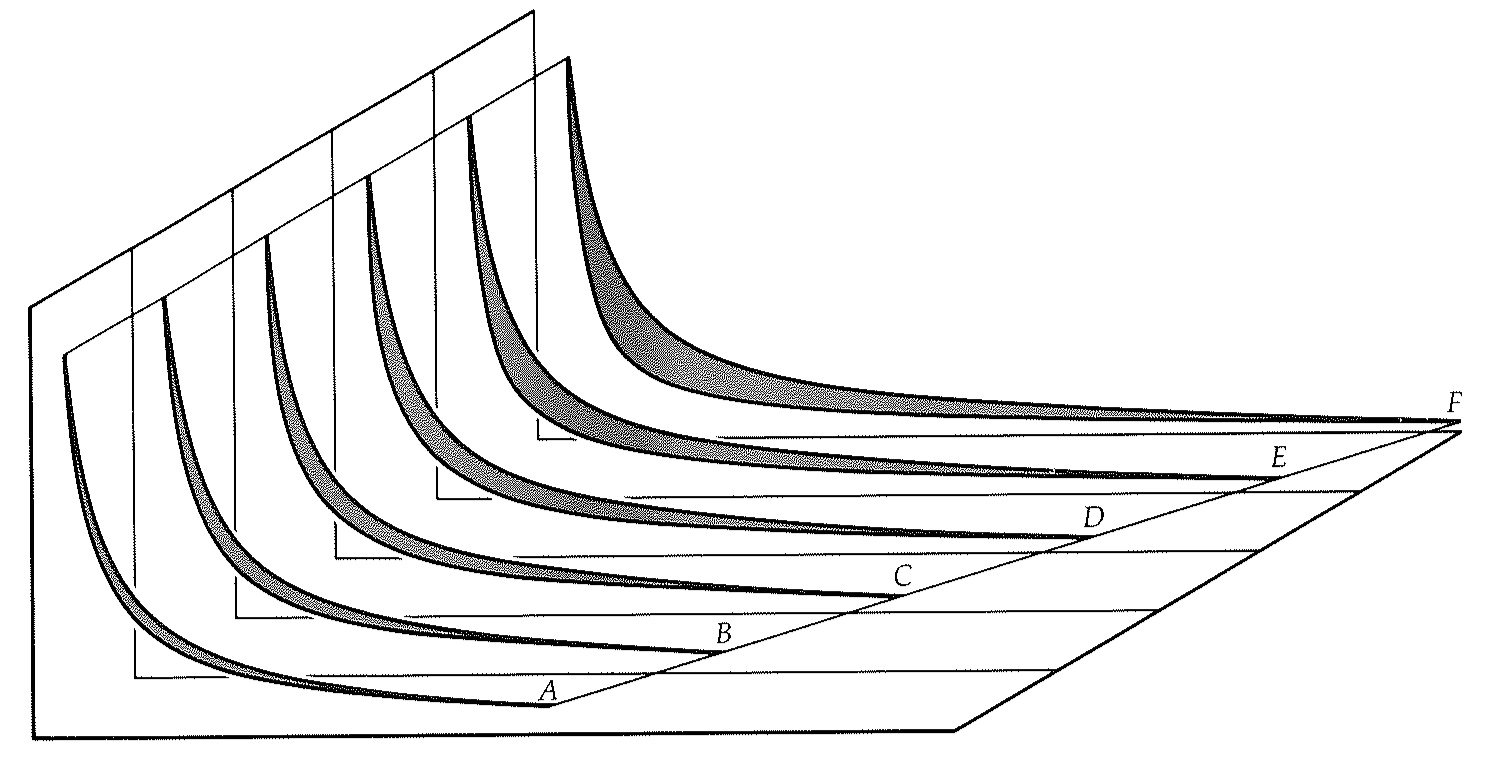
Carnot indicator diagrams for cycles with decreasing cold-sink temperatures ($F$ is coldest) but constant heat imput. The work output (shaded area) increases, and therefore so does the efficiency, but the stroke required becomes large.

The Third Law of thermodynamics generalizes this result. In a dejected kind of way it summarizes experience by the following remark:

Third Law: Absolute zero is unattainable in a finite number of steps.

This gives rise to the following sardonic summary of thermodynamics:

First Law: Heat can be converted into work.

Second Law: But completely only at absolute zero.

Third Law: And absolute zero is unattainable!

The End of the External

We have traveled a long way in this chapter. First, we drew together the skeins of experience summarized by the Kelvin and the Clausius statements of the Second Law, saw that they were equivalent, and exposed two faces of Nature’s dissymmetry. We also saw that we could draw the two statements together by introducing a property of the system not readily discernable to the untutored eye, the entropy. We have seen that the entropy may be measured, and that it may be deployed to draw far-reaching conclusions about the nature of change. We have seen that the Universe is rolling uphill in entropy, and that it is thriving off the corruption of the quality of its energy.

Yet all this is superficial. We have been standing outside the world of events, but we have not yet discerned the deeper nature of change. Now is the time to descend into matter.

---

3 COLLAPSE INTO CHAOS

Matter consists of atoms. That is the first step away from the superficialities of experience. Of course, we could burrow even further beneath superficiality, and regard matter as consisting of more (but perhaps not limitlessly more) fundamental entities. Perhaps Kelvin was right in his suspicion that the most fundamental aspect of the world is its eternal, elusive, and perhaps zero energy. But although the onion of matter can be peeled beyond the atom, that is where we stop; for in thermodynamics we are concerned with the changes that occur under the gentle persuasion of heat, and under most of the conditions we encounter, the energy supplied as we heat a system is not great enough to break open its atoms. The gentleness of the domain of thermodynamics is why it was among the first of scientists’ targets: only as increasingly energetic methods of exploration and destruction became available were other targets opened to inspection, and in turn, as the vigor of wars increased, so the internal structure of the atom, the nucleus, and the nucleons became a part of science. Heat, although it may burn and sear, is largely gentle to atoms.

The concept of the atom, although it originated with the Greeks, began to be convincing during the early nineteenth century, and came to full fruition in the early twentieth. As it grew, there developed the realization that although thermodynamics was an increasingly elegant, logical, and self-sufficient subject, it would remain incomplete until its relation to the atomic model of matter had been established. There was some opposition to this view; but support for it came from (among others) Clausius, who identified the nature of heat and work in atomic terms, and set alight the flame that Boltzmann soon was to shine on the world.

Although we have been speaking of atoms, in many of the applications of thermodynamics molecules also play an important role, as do ions, which are atoms or molecules that carry an electric charge. In order to cover all these species, we shall in general speak of particles.

Inside Energy

As a first step into matter we must refine our understanding of energy by recalling some elementary physics. In particular, we should recall that a particle may possess energy by virtue of its location and its motion. The former is called its potential energy; the latter is its kinetic energy.

A particle in the Earth’s gravitational field has a potential energy that depends on its height: the higher it is, the greater its potential energy. Likewise, a spring has a potential energy that depends on its degree of extension or compression. Charged particles near each other have a potential energy by virtue of their electrostatic interaction. Atoms near each other have a potential energy by virtue of their interaction (largely the electrostatic interactions between their nuclei and their electrons).

A moving particle possesses kinetic energy: the faster it goes, the greater its kinetic energy. A stationary particle possesses no kinetic energy. A heavy particle moving quickly, like a cannonball (or, in more modern terms, a proton in an accelerator), possesses a great store of energy in its motion.

The most important property of the total energy of a particle (the sum of its potential and kinetic energies) is that it is constant in the absence of externally applied forces. This is the law of the conservation of energy, which moved to the center of the stage as the importance of energy as a unifying concept was recognized during the nineteenth century. It accounts for the motion of everyday particles like baseballs and boulders, and applies to particles the size of atoms (subject to some subtle restrictions of that great clarifier, the quantum theory). For instance, the law readily accounts for the motion of a pendulum: there is a periodic conversion from potential to kinetic energy as the bob swings from its high, stationary turning point, moves quickly (with high kinetic energy) through the region of lowest potential energy (at the lowest point of its swing), and then climbs more and more slowly to its next turning point. Potential and kinetic energy are equivalent, in the sense that one may readily be changed into the other; their sum, in an isolated object, remains the same.

Intrinsic to the soul of thermodynamics is the fact that it deals with vast numbers of particles. A typical yardstick to keep in mind is Avogadro’s number. Its value is about $6\times {10}^{23}$, and it represents the number of atoms in 12 grams of carbon. (By coincidence, it is not far off the number of stars in all the galaxies in the visible Universe.) The idea to appreciate here is not the precise value of Avogadro’s number, or the precise number of atoms in any given system, but the fact that the numbers of atoms involved in everyday samples of matter are truly enormous. It may seem surprising at first sight that science learned to deal with the properties of such enormous crowds of particles before it discovered how to deal with individual atoms. The reason lies at the core of thermodynamics: the thermodynamic properties of a system are average values over statistically large assemblies of particles. Just as it is easier to deal with average properties of human populations than with individuals, be they consumers, wearers, or wage-earners, so it is easier to deal with the average properties of assemblies of particles than with the individuals. Idiosyncracies (which the atomically aware thermodynamicist terms fluctuations) are ironed out and become relatively insignificant when the populations are large, and the population of particles in a typical sample is vastly greater than the population of people of any nation.

The energy of a thermodynamic system, such as the several Avogadro’s numbers of water molecules in a glass of water, is the sum of the kinetic energies of all the particles and of their potential energies too. Hence, it should be plain that this total energy is constant (the essential content of simple versions of the First Law). However, in a many-particle thermodynamic system, a new aspect of the motion, one not open to a single particle on its own becomes available.

Consider the kinetic energy of the collection. If all the particles happen to be traveling in the same direction with the same speed, then the entire system is in flight, like a baseball (see below). The entire system behaves like a single, massive particle, and the ordinary laws of dynamics apply. However, there is another sort of motion. Instead of all the particles moving uniformly, we can think of them as being chaotic: the total energy of the system may be the same as that of the ball in flight, but now there is no net motion, because all the directions and speeds of the atoms are jumbled up in chaos (see the figure on the next page). If we could follow any individual particle, we would see it moving a tiny amount to the right, bouncing off its neighbor, moving to the left, bouncing again, and so on. The central feature is the lack of correlation between the motions of different particles: their motion is incoherent.

The particles of a ball in flight are moving coherently: they are all turned $O{N}^{\ast }$.

The same quantity of energy may be stored by a stationary but warm ball. Now the particles are moving incoherently: they are furned ON. The random, incoherent motion is called thermal motion.

This random, chaotic, uncorrelated, incoherent motion is called thermal motion. Obviously, since it is meaningless to speak of the uncorrelated motion of a single particle, the concept of thermal motion cannot be applied to single particles. In other words, when we step from considering a single particle to considering systems of many particles, when the question of coherence becomes relevant, we are stepping out of simple dynamics into a new world of physics. This world is thermodynamics. All the richness of the subject, the way that the steam engine can make the journey into life and account for the folding of a leaf, results from enlargement of domain.

We have established that there are two modes of motion for the particles of a composite system: the motion may be coherent, when all the particles are in step, or the motion may be incoherent, when the particles are moving chaotically. We have also seen in our encounter with the First Law that there are two modes of transferring energy to a system, by doing work on it or by heating it. Now we can put the remarks together:

When we do work on a system, we are stimulating its particles with coherent motion; when the system is doing work on the surroundings, it is stimulating coherent motion.

When we heat a system, we are stimulating its particles with incoherent motion; when a system is heating its surroundings, it is stimulating incoherent motion.

Work involves the transfer of energy by using the coherent motion of particles in the surroundings (left illustration). The particles in the system will pick up the coherent motion, and might dissipate it into thermal motion. Heat is the transfer of energy by using the incoherent motion of particles in the strroundings (right illustration). They jostle the particles of the system into incoherent thermal motion.

This distinction is illustrated above. A couple of examples should make this clear. Suppose we want to change the energy of a 1-kilogram block of iron (a cube about $5\mathrm{cm}$ on each side). One way would be to lift it: lifting it through 1 meter increases its potential energy by about 10 joules (Appendix 1). What we have done is move all its atoms coherently through a displacement of 1 meter. Energy has been transferred to the block, and is now stored in the gravitational potential energy of all its atoms. Energy has been transferred by doing work.

Suppose instead that the block is hurled off in some horizontal direction. Now the kinetic energy of all its atoms has been increased and their motion is coherent. If they all move at $4.5$ meters per second (about 10 m.p.h.), the block acquires 10 joules of energy. Energy has been transferred to the block, and is now stored in the kinetic energy of all its atoms. Once again, energy has been transferred by doing work.

Now suppose we expose the block to a flame, and raise its temperature. This increases its energy, but the block remains in its initial position and seems not to be moving. However, if the temperature is raised by only $0.03{}^{\circ }\mathrm{C}$, the transfer will correspond to 10 joules of energy, exactly as before. Now the energy is stored in the thermal motion of the atoms. It is still stored as their kinetic and potential energies (the only form of energy storage we ever need consider), but now the locations and motions of the atoms are incoherent, and there is no net displacement or motion of the block as a whole. Energy has been transferred to the block by stimulating the incoherent motion of its atoms. Energy has been transferred by heating the block.

The Mark I universe. Each rectangle represents an atom; there are 1,600 in all.

Modelling the Universe

An atom of the model universe that is storing energy is said to be “ON”: $\mathrm{ON}$-ness is denoted by red, OFF-ness by white. The ON atoms an be thought of as vibrating incoherently, and as having exactly the same energy as any other atom that is $\mathrm{ON}$

The Universe is quite a complicated place, but there are a lot of simple things going on inside it. In much of the following discussion, it will prove useful to focus on the essential features of the processes without getting distracted by complications like dogs, opinions, and other trappings of reality. Of course, we must always ensure that the simplification doesn’t destroy important details; so we shall swing frequently between the very simple models of the Universe and the actual Universe, in which simplicities are sometimes so cloaked in consequences that their true natures are obscured. When we refer to a model of the Universe, we shall call it a “universe”.

We shall use two simple models of the Universe. The Mark I universe consists of up to 1,600 atoms (see above).* Each atom may be energetically unexcited, which we shall call OFF, or energetically excited, which we shall call ON. In the illustrations we shall denote ON-ness by a red blob (see figure on left).

• The universe has been given this number of atoms for a special reason: 1,600 is the number of blobs on a low-resolution graphics screen of an Apple computer. The illustrations that follow, and the calculations behind some of the numbers, have been prepared on an Apple Ile. Some of the primitive programs used are listed in Appendix 3. By using them, you will be able to explore the properties of the universe in the manner we shall gradually unfold.

An atom of the model tuiverse that is storing energy in a way that is correlated with the energy stored in other atoms (for instance, in tuiform motion) is said to be ${\mathrm{ON}}^{\ast }:{\mathrm{ON}}^{\ast }$-ness is denoted by a red arrow. Once again, each atom can store a single characteristic quantity of energy.

When several atoms are ON, we shall take their motions to be uncorrelated unless specified. That is, several red blobs in the region of the universe that represents some system means that the atoms are storing their energy as thermal motion. When we want to indicate that the motion of a group of atoms is coherent, we shall say that the atoms are ${\mathrm{ON}}^{\ast }$ and denote them by red arrows in the direction of their motion (see figure on left). Another simplifying feature of the Mark I universe is that each atom can possess only a single characteristic energy when it is $\mathrm{ON}$, and this quantity is the same for each atom. (We could think of the energy required to turn an atom $\mathrm{ON}$ as being 1 joule, although that would correspond to a cannonball of an atom. If a hydrogen atom is supplied with only ${10}^{-18}$ joules, it falls apart. The actual value will not be important for most of what follows; so we can adopt the simplest value in order to have something concrete, or just leave it unspecified if something more concrete is not needed.)

The Mark II universe is the same as the Mark I version, except that the number of atoms in it is infinite: we can still use the 1,600 blobs to show atoms, but now this represents only a minute fraction of the total universe (see below).

This is the universe we use when we want to model the reservoirs we mentioned in Chapter 2: they are insatiable sinks and inexhaustible sources.

The Mark III universe (see figure on next page) we shall hold in reserve for now: it has more complicated entities, such as atoms that can possess various quantities of energy, atoms of different kinds, concatenations of atoms, and even people.

The Mark II universe is like the Mark I version, but it has an indefinitely large number of identical atoms.

The Mark III universe is much more complicated: it has all sorts of atoms strung together in complex patterns. Nevertheless, the underlying processes are no more complex than the ones possessed by the earlier Marks.

Now we put the Mark I universe into operation and see what it reveals about the process of change. The only rule we shall impose is the conservation of energy in the universe as a whole (so that the number of atoms ON remains constant). We shall allow any atom to hand on its $\mathrm{ON}$-ness to a neighbor, or pick up energy, and so turn $\mathrm{ON}$, from a neighbor that happens to be $\mathrm{ON}$ already. (An atom cannot be more than $\mathrm{ON}$ or partially $\mathrm{ON}$ : one $\mathrm{ON}$ per atom at most; and either $\mathrm{ON}$ or OFF.)

In terms of an actual process in the Universe, we can think of the gray area in the figure on the facing page as representing one block of iron, and the untinted area as representing another. Then the state of being $\mathrm{ON}$ represents an atom that is vibrating vigorously around its average location, and an atom that is OFF represents an atom that is motionless. The handing on of $\mathrm{ON}$-ness then corresponds to an $\mathrm{ON}$ atom jostling a previously motionless neighbor, which breaks into vibration at the expense of the energy of the previously vibrating atom. This handing on of vibrational motion is a random process, and so $\mathrm{ON}$-ness just wanders at random from atom to atom.

The initial state of a Mark I universe modeling two blocks of metal in contact. No atoms in the bigger (L-shaped) block are $ON$, and all the energy of the tuiverse resides in the smaller block, which is hot. Using the formula we give later, we can calculate that the temperature of System 1 is $2.47$ and that of System 2 is zero.

The central point about the behavior of the universe, and by extension of the Universe too, is that properties arise from the minimum of rules. The only rule we are adopting is the conservation of $\mathrm{ON}$-ness. We are allowing undirected and unconstrained mobility. Even with this light touch, the universe possesses properties. The same properties could be contrived by imposing rules, such as the rule that energy shall migrate from atom to atom in a specified manner. But such rules are plainly unnecessary, and the scientific razor cuts them out.

Suppose we have the arrangement of $\mathrm{ON}$-ness in the universe as depicted above. This corresponds to a lot of energy stored in the thermal motion of System 1 (one block of iron), and none at all in System 2 (the other block). What will happen?

As the excited atoms of System 1 wobble, they bump into each other, and any one can pass its energy on to any of its neighbors. If this happens, then the first atom turns OFF, and the second turns $\mathrm{ON}$. The newly $\mathrm{ON}$ atom is itself now wobbling and jostling its neighbors, and so it may exchange energy with them. The energy, the ON-ness, therefore wanders aimlessly through the system and may arrive at its edge.

At the edge where System 1 touches System 2, the jostling takes place just as it does inside the system itself. An excited atom on the face of System 1 can jostle an atom on the face of System 2, and turn the latter ON. This $\mathrm{ON}$ atom jostles its neighbors, and so the energy migrates at random into and through System 2. In this way the thermal motion of the atoms in System 2 is stimulated, but at the expense of System 1. That is, System 2 is heated by System 1, and the latter cools (see top figure on next page).

Some time after the initial stage, the energy is spread more uniformly over all the atoms as a result of their jostling each other. The small block still has a higher proportion of its atoms ON than the bigger block, and so it is still hotter. The temperature of System 1 is now $0.72$ and that of System 2 is $0.23$.

What is the final state of the universe? There is no final state for the careful observer, for the $\mathrm{ON}$-ness jostles and migrates forever (there is no rule that brings it to an end). But there is an apparent final state for an observer who stands so far back that the behavior of the individual atoms cannot be discerned. There is a final state for the thermodynamic observer, not for the atomic individualist. This apparent end of change occurs when there is a uniform distribution of ON-ness, as in the figure below.

Later, the jostling of the atoms results in a uniform distribution of the energy. There will be small accumulations here and there (there are fluctuations), but on average the proportion of atoms $ON$ in the smaller block is equal to the proportion $\mathrm{ON}$ in the larger. The temperatures of the blocks are now the same, at 0.27, and they are at thermal equilibrium.

The sequence of illustrations on the two preceding pages shows how the universe attains not so much a final state as a steady state. In this state the individual atoms turn $\mathrm{ON}$ and $\mathrm{OFF}$ as they have always done, but, to the casual observer of averages, the redistribution of energy leaves the universe apparently unchanged. We see that the jostling, random migration of energy disperses it. When it is uniformly dispersed over the available universe, it remains dispersed.

That last remark is not quite true, because the random wandering of ON-ness may lead it to accumulate, by chance, in System 1 and leave Sytem 2 completely OFF. However, even with a universe of 1,600 atoms this chance is slight (as may be tested by using one of the programs), and in a real Universe, where each system is a block of Avogadro’s numbers of atoms, the chance is so remote that it is negligible. Lack of rules allied with vastness of domain accounts for the virtual irreversibility of the process of dispersal.

Temperature

Before we wrap this observation into a neat package, let us notice that we are also closing in on the significance of temperature. We have just seen that System 1 heats System 2 as a natural consequence of the dispersal of energy, and that the net transfer of energy continues until, on average, the energy is evenly dispersed over all the available atoms. Now note the following important distinction. When the ON-ness is evenly distributed, there is more energy in System 2 than in System 1 (because the former contains more atoms, and therefore more are ON when the ON-ness is uniformly distributed), but the ratio of the numbers $\mathrm{ON}$ and $\mathrm{OFF}$ is the same in both.

All this conforms with common sense about hot and cold so long as we interpret the ratio of the numbers of atoms $\mathrm{ON}$ and $\mathrm{OFF}$ as indicating temperature. First, we know that energy flows as heat from high temperatures to low, and we have seen that System 1 (which initially has a higher “temperature” than System 2) heats System 2. Second, the steady state, when there is no net flow of energy between the two systems, corresponds to their having equal “temperatures”, not equal total energies. Finally, “temperature” measures the incoherent motion, not the coherent motion, of particles; it is intrinsically a thermodynamic (as distinct from a dynamic) property of systems of many particles. It would be absurd to refer to the temperature of a single particle. When we say that a baseball is warm, we are referring to the excitation of its component particles, not to the whole baseball regarded as a single particle.

Temperature reflects the ratio of the numbers of atom ON and OFF: the higher the ratio, the higher the temperature. This interpretation carries over into the actual Universe, where high temperatures correspond to systems in which a high proportion of particles are in excited states. Notice once again the sharp distinction between the temperature of a system and the energy it may possess: a system may possess a large quantity of energy, yet still have a low temperature. For instance, a very large system may have a low proportion of its atoms ON, and therefore be cool; but there are still so many atoms that the sum of their energies is large, and so overall the system possesses a lot of energy. The oceans of the Earth, although they are cool, are immense storehouses of energy. The energy of a system depends on its size; the temperature does not.

A further point is more in the nature of housekeeping. The concept of temperature entered thermodynamics along a classical route; it would be a remarkable piece of luck if the classical definition had turned out to be numerically the same as the ratio of numbers of $\mathrm{ON}$ and OFF. The best we can reasonably expect is that increasing temperature in the classical sense corresponds to increasing ratio of $\mathrm{ON}$ to $\mathrm{OFF}$ in the atomic sense. We cannot assume they will increase in precisely the same way; temperature might increase as the square (or some other increasing function) of the ratio, and not directly as Number ${}_{\mathrm{ON}}/$ Number ${}_{\mathrm{OFF}}$ itself.

We have seen that classical thermodynamics, speaking about the efficiencies of engines, imposes a lower bound to temperature: there is an absolute zero of temperature. In the atomic interpretation, we would expect this to correspond to a system in which no atoms at all are $\mathrm{ON}$ (as in the initial state of System 2, depicted in the figure on page 53). Since there cannot be fewer than no atoms $\mathrm{ON}$, the atomic approach to temperature neatly corroborates the classical expectation of a lower bound to temperature. This is just one example of how the atomic interpretation leads to straightforward explanations of classical conclusions.

It turns out that the thermodynamic and atomic versions of temperature coincide in all respects-the temperature goes up if the ratio goes up; the temperature is zero if no atoms are $\mathrm{ON}$; the thermodynamic expressions relating temperature, energy, and entropy all work-if temperature is related to the ratio by

$$\mathit{\text{Temperature}}=A/\log \left({\mathit{\text{Number}}}_{OFF}/{\mathit{\text{Number}}}_{ON}\right)$$

where $A$ is a constant that depends on how much energy is needed to turn an atom $\mathrm{ON}$. If for convenience we arbitrarily set $A$ equal to unity, then the temperatures given by this expression are pure numbers (we could choose $A$ to have the units of kelvins, as described in Appendix 2, but that is an unnecessary complication here).

The fluctuations of the temperatures of the two blocks: the green points refer to the large system, the orange to the small. The calculation has been done on the assumption that 100 atoms of the thiverse are $\mathrm{ON}$, and the location of each $\mathrm{ON}$-ness is random from one moment to the next. Note that the larger (1,500 atom) system has smaller fluctuations. The two temperatures fluctuate around the same mean in each system. In a system of ordinary size, the fluctuations would be insignificantly small.

By evaluating the preceding formula for appropriate values of numbers $\mathrm{ON}$ and $\mathrm{OFF}$, we can ascribe temperatures to the states of the universe illustrated in the figures on pages 53 and 54. The important point to notice is that the temperatures of the two systems converge to a value intermediate between their two initial values. Then, once they have reached equality of temperature, there they remain, except for chance fluctuations, forever. Using the computer programs, we can in fact map the fluctuations: they are shown in the figure above. Sometimes they are quite large, especially for the smaller system (and so we would notice it jumping between hot and cold around some average temperature); but that is because the systems, and especially the fragment we are calling System 1 , are so small. A much larger system would show far smaller fluctuations of temperature at equilibrium; an infinite system would show virtually none.

The Direction of Natural Change

In a very natural way, without imposing superfluous rules, and whittling regulations to the bone, we have arrived at an explanation of the direction of at least one natural change. We have stumbled across one wing of the Second Law. Simply by accepting that jostling atoms pass on their energy at random, we have accounted for one class of phenomena in the world. In fact, this identification of the chaotic dispersal of energy as the purposeless motivation of change is the pivot of the rest of the book. The Second Law is the recognition by external observers of the consequences of this purposeless tendency of energy.

A preliminary working statement of the Second Law in terms of the behavior of individual atoms is therefore that energy tends to disperse. (We shall refine the statement as we assemble more information.) This is not a purposeful tendency: it is simply a consequence of the way that particles happen to bump into each other and in the course of the collision happen to hand on their energy. It is a tendency reflecting unconstrained freedom, not intention nor compulsion.

At this stage we have seen only the tip of the iceberg of the processes involved in natural change, but as we go on we shall increasingly come to recognize that the simple idea of energy dispersing accounts for all the change that characterizes this extraordinary world. When we grasp that energy disperses, we grasp the spring of Nature. It should also be more apparent now that the Second Law is a commentary about events that are intrinsically simpler than those treated by the First Law. The latter is concerned with establishing the concept of energy, something that (it seems to me) remains elusive even after we have analyzed it into its kinetic and potential contributions: after all, what are they? Perhaps that elusiveness is appropriate for a concept so close to the Universe’s core. The Second Law, on the other hand, regards the energy as an established concept, and talks about its dispersal. Even though we might not comprehend the nature of energy, it is easy to comprehend what is meant by its dispersal.

The interpretation of the Second Law that we have now partially established relates to the Clausius statement, which denies the possibility that heat will travel spontaneously up a temperature gradient. The dispersal interpretation simply says that energy might by chance happen to travel in such a way that it ends up where there is already a higher proportion of atoms ON (see below), but the likelihood is so remote that we can dismiss it as impossible. But what of the Kelvin statement of the Second Law: how is dispersal related to the conversion of heat to work?

The migration of energy into a region of the universe that already has a higher proportion of its atoms $ON$ is very unlikely. This is the microscopic basis of the Clausius statement of the Second Law.

In order to capture the interconversion of heat and work, we have to remember their distinction: work involves coherent motion; heat involves incoherent motion. The atomic basis of the dissymmetry in their freedom to interconvert can be identified by thinking about a familiar example.

Think of a bouncing ball. Everyone knows that a bouncing ball eventually comes to rest. No reliable witness has ever reported, and almost certainly no one has ever observed, the opposite change, in which a resting ball spontaneously starts to bounce, and then bounces higher and higher. This would be contrary to the Kelvin statement, because if we caught the ball at the top of one of its bounces, we could attach it to some pulleys, and lower it to the ground (see below). In doing so we could extract its energy as work. Since that energy came from the warmth of the surface on which it was initially resting (because we are not questioning the validity of the First Law: this is Jack’s game again), we would have succeeded in converting heat into work, and the ball is back where it began. That possibility is denied by the Kelvin statement. Therefore, if we can use the idea of the dispersal of energy to account for the absence of reliable reports of balls that spontaneously bounce more vigorously, we shall capture Kelvin as well as Clausius in our net.

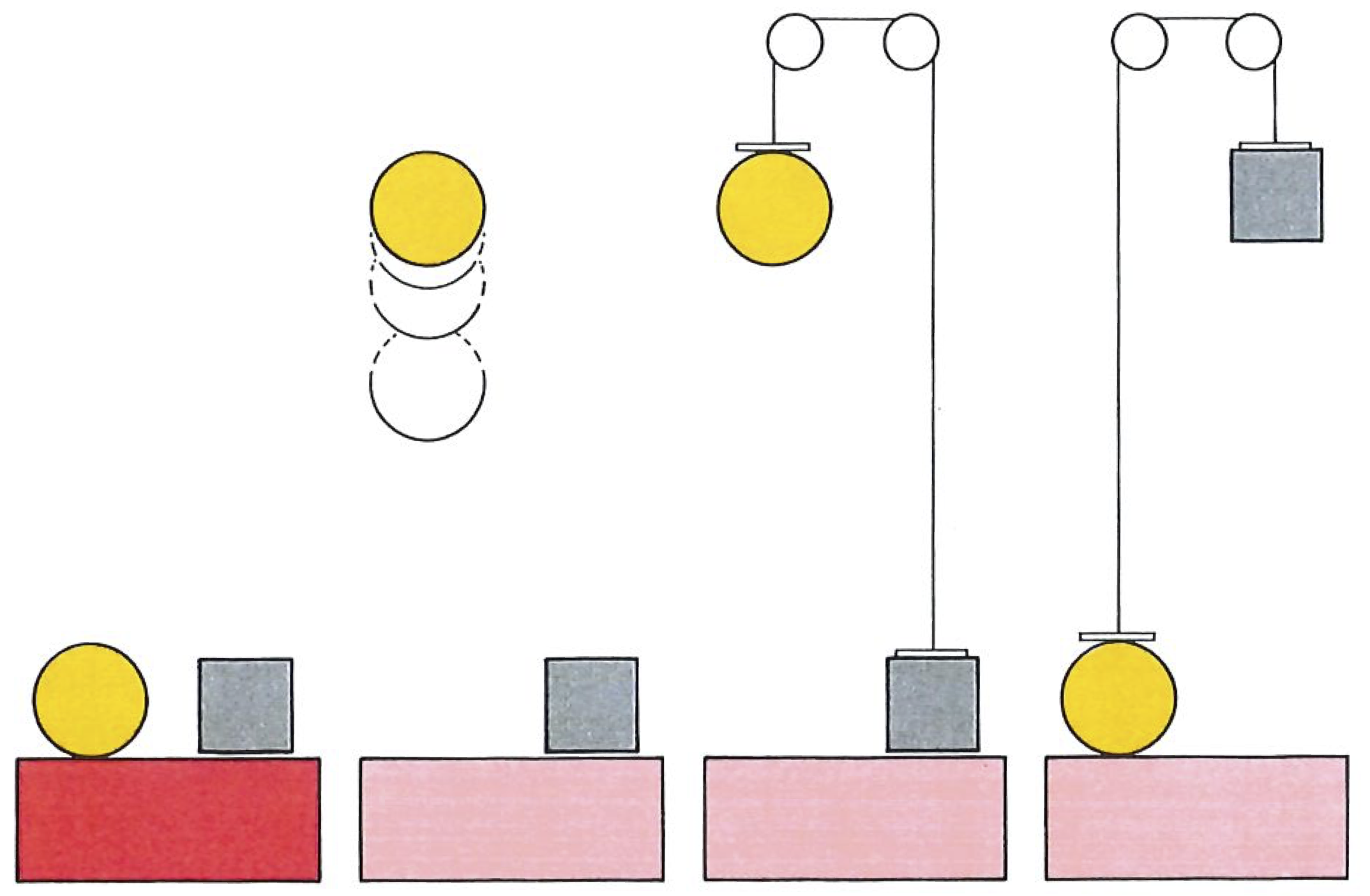
The steps involved in harnessing a bouncing ball for work. On the left, the ball and a weight rest on a warm table. The ball bounces up at the expense of the energy stored in the thermal motion of the particles of the table. At the top of its flight, it is captured and joined to the weight by a cord. As the heavy ball falls, it raises the weight. The overall process is the raising of a weight (that is, work has been done) at the expense of some heat, which contradicts the Kelvin statement.

The model of the bouncing ball in the model universe.

The moment of impact of the ball with the table. At a microscopic level, the impacts are not all head-on, and some of the coherent motion is degraded into thermal motion.

A bouncing ball consists of a collection of coherently moving atoms. The bundle of atoms moves coherently upward, slows down, changes direction, and moves coherently downward. If the ball is warm, the atoms also possess energy by virtue of their thermal motion, but we need not trouble about that initially. The motion of the ball can be modeled in the universe as shown above.

In the collision when the ball strikes the table, energy is transferred between the two sets of atoms (and among the atoms of each set). As a result, the atoms of the ball reverse their direction, rise off the table, and climb away. As they do so, their kinetic energy converts to potential; the ball gradually slows, then turns, and drops again.

However, not all the kinetic energy that the ball possessed immediately before the collision remains in it in the form of coherent motion. Some of this energy jostles out while its atoms are in contact with those of the table, and even some that remains becomes randomized in direction.

How this happens even in a head-on collision is illustrated in the figure on the left, which shows that what to the ordinary observer seems to be head-on, in fact, on an atomic scale, involves various particles approaching each other over a wide range of angles, and so the motion is transferred in random directions. (A coherent motion as well as a chaotic motion, of the atoms of the table will also be stimulated, because at the point of contact of through the solid. Nevertheless, this band of squashed atoms gets randomized as it moves, and in due course decays into thermal motion. A similar fate awaits the compression wave through the surrounding air, the wave that gives rise to the sound of the ball hitting the table.)

Successive bounces of the model ball. Initially (left) the motion is coherent. After the first impact (middle), some of the coherently stored energy has become incoherent. After several bounces, all coherence has been lost, and the energy is stored as incoherent thermal motion, with ON-ness uniformly distributed over the entire tuiverse of ball and table.

The upshot of this discussion is that each time the ball hits the table, the coherent motion of its atoms is slightly degraded into the thermal motion of its atoms and the atoms of the rest of the universe. This is shown by the atoms turning $\mathrm{ON}$ in the ball and the surface (denoted by the yellow blobs above). As they turn $\mathrm{ON}$ the coherent motion gradually turns OFF. Therefore, after each bounce the surface and the ball are a little warmer because the impacts have stimulated the thermal motion at the expense of the coherent. The coherent motion of the atoms of the ball gradually degrades into the incoherent motion of the atoms of the universe. If we wait long enough, all the original coherent motion will have degraded into incoherent motion, and that incoherent motion will be uniformly distributed throughout the universe. The slightly warmer ball will be at rest on the slightly warmer table; moreover, the ball and table will be at the same temperature, for the ON-ness will have dispersed uniformly. The kinetic energy of the ball has been dissipated in the thermal motion. Coherence has collapsed into incoherence.

The reverse of this sequence is exceedingly unlikely to occur naturally. We can think of the ball sitting on the warm table. Its atoms and those of the table are wobbling around their mean positions, and there is plenty of energy to send it flying up into the air. However, there are two reasons why the energy is not available.

One problem is that the energy is distributed over all the atoms of the universe. Therefore, in order for the ball to go flying off upward, a good proportion of the dispersed energy must accumulate in the ball. This is not particularly likely to occur, because the $\mathrm{ON}$-ness of the atoms is wandering around at random, and the chance of enough of it being in the ball simultaneously is very slight. The length of time we would have to wait can be explored by using the Fluctuation program in Appendix 3, which runs through the random jostling of a universe like that shown above. In a real Universe, with so many atoms, we would probably need to wait a good fraction of eternity before seeing even such an insignificant miracle as a spontaneously bouncing ball, and matter would almost certainly decay first.

But in fact the reasons go deeper, for the ball could be put on a hot surface. We have already seen that a 1-kilogram block of iron can rise 1 meter above the surface of the Earth if we transfer 10 joules of energy to it, and such a quantity of energy can readily wander in if the block stands on a slightly hotter surface. But even cool balls placed on hot surfaces do not rise spontaneously into the air. Why? Because the accumulation of energy in the ball, the ON-ness of its atoms, is only a necessary condition for it to be able to rise into the air: it is not a sufficient condition. In order for the ball to rise, the atoms must be not merely $\mathrm{ON}$, but ${\mathrm{ON}}^{\ast }$; that is, the energy must be present as coherent motion of the atoms, not merely as incoherent thermal motion. Even if sufficient energy were to wander into the ball from the surroundings, it would be exceedingly unlikely to switch all the atoms ${\mathrm{ON}}^{\ast }$ and induce coherent motion.

Now we are at the nub of the interpretation of the Kelvin statement of the Second Law. The concept of dispersal must take into account the fact that in thermodynamic systems the coherence of the motion and the location of the particles is an essential and distinctive feature. We have to interpret the dispersal of energy to include not only its spatial dispersal over the atoms of the universe, but the destruction of coherence too. Then energy tends to disperse captures the foundations of the Second Law.

Natural Processes

The natural tendency of energy to disperse-that is, to spread through space, to spread the particles that are storing it, and to lose the coherence with which the particles are storing it-establishes the direction of natural events. The First Law allows events to run contrary to common experience: under its rule alone, a ball could start bouncing at the expense of cooling, a spring could spontaneously become compressed, and a block of iron could spontaneously become hotter than its surroundings. All these events could occur without contravening the conservation of energy. However, none of them occurs in practice, because although the energy is present it is unavailable. Energy does not, except by the remotest chance, spontaneously localize and accumulate in a large excess in a tiny part of the Universe. And even if energy were to accumulate, there is little likelihood that is would do so coherently.

Natural processes are those that accompany the dispersal of energy. In these terms it is easy to understand why a hot object cools to the temperature of its surroundings, why coherent motion gives way to incoherent, and why uniform motion decays by friction to thermal motion. It should be just as easy to accept that, whatever the manifestations of the dissymmetries identified by the Second Law, they are aspects of dispersal. As energy collapses into chaos, the events of the world move forward. But in Chapter 2 we saw that change is accompanied by an increase of entropy. Entropy must therefore be a measure of chaos. Moreover, we have seen that the natural tendency of events corresponds to the corruption of the quality of energy. Consequently, quality must reflect the absence of chaos. High-quality energy must be undispersed energy, energy that is highly localized (as in a lump of coal or a nucleus of an atom); it may also be energy that is stored in the coherent motion of atoms (as in the flow of water).

We are on the brink of uniting these concepts. We have a picture of what it means for the spring of the world to unwind; now we must relate this picture to the entropy. As we do so, we shall acquire Boltzmann’s vision of the nature of change.

---

4 THE ENUMERATION OF CHAOS

Boltzmann’s tomstone in the central cementery of Viena. The equation in the inscription reads $S=k\log W$.

Carved on a tombstone in the central cemetery in Vienna is an equation. It is not only one of the most remarkable formulas of science, but also the ladder we need to climb from the qualitative discussion of the dispersal of energy up to the quantitative. The tombstone marks Boltzmann’s grave. The formula to the left is our ladder and his epitaph.

Boltzmann’s epitaph summarizes most fittingly his work. The letter $S$ denotes the entropy of a system. The letter $k$ denotes a fundamental constant of Nature now known as Boltzmann’s constant (in what follows we do not need its actual value; so we shall pretend it is equal to unity). The letter $W$ is a measure, in a sense that we shall shortly unfold, of the chaos of a system. Here is our first encounter with a formula that has as many implications for the modern world as Einstein’s $E=m{c}^2$ (the only other equation that people in general seem prepared to know).

Boltzmann’s equation is central to our discussion because it relates entropy to chaos. On its left we have the entropy, the function which entered thermodynamics in the train of the Second Law and which is the classical signpost of spontaneous change. On the right we have a quantity that relates to chaos because it measures the extent to which energy is dispersed in the world; the concept of energy dispersal, as we have just seen, is the heart of the microscopic mechanism of change. $S$ stands firmly in the world of classical thermodynamics, the world of distillations of experience; $W$ stands squarely in the world of atoms, the world of underlying appearance and its underworld of atoms.

As Chapter 2 refined the observations discussed in Chapter 1 that gave rise to the perception that energy possesses quality as well as quantity, so this chapter will refine the qualitative discussion of dispersal we met in Chapter 3 . Clausius himself saw what we have already seen: he saw the difference between heat and work, understood the intrinsic incoherence of thermal motion, and appreciated what was meant and what was implied by degradation and dispersal of energy. But the world is indebted to Boltzmann for refining that view into an instrument as sharp as a Japanese sword, and showing us how to cut numbers from chaos.

The program of this chapter is to extend and sharpen the blade we have begun to form: we have to enumerate chaos and see numerically, rather than merely intuitively, that natural events represent collapse into chaos and that, in a quantitatively precise sense, events are motivated by corruption.

Boltzmann’s Demon

How can we quantify chaos? What is the meaning of W? We can arrive simultaneously at both answers by considering a special initial case of the Mark I universe and allowing it to run through its subsequent history. The special initial state is shown below: every atom in System 1 is $\mathrm{ON}$; every atom of System 2 is OFF.

A state of the Mark I universe in which all atoms of System 1 are $ON$, and all atoms of System 2 are OFF.

The question we now ask is the following: how many ways can the inside of a system be arranged without an external observer being aware that rearrangements have occurred? The answer is what is meant by the quantity $W$. Notice how this captures what we have earlier called the essential step in going from atoms to systems, an observer’s blindness to individuals. Thermodynamics is concerned with only the average behavior of great crowds of atoms, and the precise role being played by each one is irrelevant. If the thermodynamic observer doesn’t notice that change is occurring, then the state of the system is regarded as the same: it is only the minutely precise observer who insists on scrutinizing individual atoms who knows that change is actually in progress.

We shall imagine a Demon, a little, insubstantial, neuter, mischievous, and eternally busy thing. I shall call it Boltzmann’s Demon${}^{\ast }$. Its busyness consists of forever reorganizing. In the universe it simply rearranges $\mathrm{ON}$ ness and OFF-ness. It is the incarnation of the lack of rules that rules the universe. Being infinitely disorganized, all it does is to relocate $\mathrm{ONs}$ at random, moving them perpetually but aimlessly.

• J. C. Maxwell had a Demon too, Maxwell’s Demon. Its mischief is quite different from Boltzmann’s Demon’s, and the two should not be confused.

We, the thermodynamically shortsighted observer, cannot see the Demon. However furiously it reorganizes, so long as it does not change the number of $\mathrm{ON}$ atoms in a system (and we note that it can only move $\mathrm{ON}$ ness, not create it), then we cannot see that it is active, or even that it is there. Boltzmann’s $W$, then, is the number of different arrangements his Demon can stumble into without us being aware that changes are afoot. If, however, the Demon does manage to move an ON out into System 2, then we shall know that it has happened: the temperature of System 1 will have dropped, and that of System 2 will have risen. We the shortsighted can see our thermometers.

In the special initial state of the universe that we are considering, the Demon cannot do anything without our noticing. All the atoms are ON in the system, and so ON-ness cannot be shifted around within it. Since there is only one arrangement possible in which all the atoms in System 1 are $\mathrm{ON}$, we conclude that $W=1$. Since the logarithm of unity is zero, Boltzmann’s equation gives us the entropy of this state of System 1 as zero. There is zero entropy in this highly localized, tidy collection of energy; so it has perfect quality.

One ON-ness has escaped from System 1 into System 2: the resulting OFF in System 1 can be in 100 different places; the single $\mathrm{ON}$ in System 2 can be in 1,500 different places.

In due course the Demon will succeed in moving one ON-ness into the other system (see the figure on the following page). This is the dawn of the Demon’s day. Now it can rearrange the ON-ness within System 1 in many different ways, and we the external observer will be none the wiser. It is quite easy to calculate the new value of $W$ : it is equal to the number of different ways of choosing which atom is to be OFF. There are 100 atoms in System 1, and as the Demon moves $99\mathrm{ON}$-nesses around, there are 100 places for the location of the one OFF. That is, $W=100$ : this state of the system is one that the Demon can arrange in 100 different ways. Then, since the natural logarithm${}^{\ast }$ of 100 , $\ln 100$, is $4.61$, Boltzmann’s epitaph gives the entropy of this state as $4.61$. The entropy of System 1 is greater than before; the system is more chaotic because we do not know the location of just one OFF.

• The expression $\log x$ is now conventionally understood to mean a logarithm to the base 10. We always work here with natural logarithms, logarithms to the base $e;e$ is a certain irrational number, $2.78$… , that is, a nonrepeating decimal like $\pi$. It was arrived at because it enables a great simplification of important types of calculations.

In due course the Demon will succeed in turning another atom OFF in System 1 and transferring its energy to an atom of System 2. Now there are two gaps in the ON-ness of System 1, and the Demon has more scope for its invisible mischief. The number of ways of arranging the $98\mathrm{ON}$-nesses it has at its disposal in System 1 is the same as the number of arrangements of the two OFFs it now must have there. One of these OFFs can turn up at any of the 100 sites; the second can turn up at any of the remaining 99 sites (see the figure on the facing page). Therefore the total number of arrangements of ON-ness that the Demon can succeed in stumbling into is $100\times$ $99=9,900$. However, some of these arrangements are identical. For instance, the Demon could first turn OFF atom 23 and then turn OFF atom 32 , or it could first turn OFF atom 32 and then atom 23 . The end result in each case is the same: atoms 23 and 32 are OFF. Therefore we should divide the previous number by 2 , because only half the 9,900 arrangements are different. This means that $W=4,950$, and that the Demon has 4,950 different ways of reorganizing System 1 without us knowing that anything is going on. Using Boltzmann’s tomb, we find that the entropy of System 1 has risen to $\ln 4,950=8.51$.

At this stage, two ON-nesses have stumbled out into System 2. There are $(100\times 99)/2$ different ways of distributing the two resulting OFFs in System 1, and $(1,500\times 1,499)/2$ different ways of distributing the two $\mathrm{ONs}$ in System 2.

We must not forget that the entropy of System 2 is increasing. Initially it was zero, because no atom was $\mathrm{ON}$, and there is then only one arrangement. Then, when the Demon happened to ship out one ON-ness from System 1 to System 2, one atom turned ON. In System 2 there are 1,500 locations for ON, and so the number of undetectable and indistinguishable ways of arriving at this thermodynamic state of System 2 is 1,500; its encommodate one can be in 1,500 locations, the are two ON-nesses to accommodate one can be in 1,500 locations, the other in any of the remaining arrangements is half of $1,500\times 1,499$, or $1,124,250$. This is the different different ways in which the thermodynamic state of System 2 can be achieved. The entropy of this state is the logarithm of this number: $\ln$ $1,124,250=13.93$. Notice that the entropy of System 2 is increasing more rapidly than the entropy of System 1: because System 2 is larger than System 1, a single ON-ness in System 2 can be located at more sites than in System 1: the Demon has more scope for rearrangement when it has more atoms to turn $\mathrm{ON}$ and $\mathrm{OFF}$.

We could continue to calculate the numbers of arrangements that the Demon can explore, and then take logarithms to arrive at the corresponding entropies. Numbers get very large, but the advantage of taking logarithms is that they cut big numbers down to small: logarithms are very lazy numbers. (For instance, the natural logarithm of 100 is $4.61$; the natural logarithm of Avogadro’s number is 54.7, even though the number itself is more than ${10}^{23}$.) Therefore, although numbers of arrangements may become astronomical, the corresponding entropies remain terrestrial.

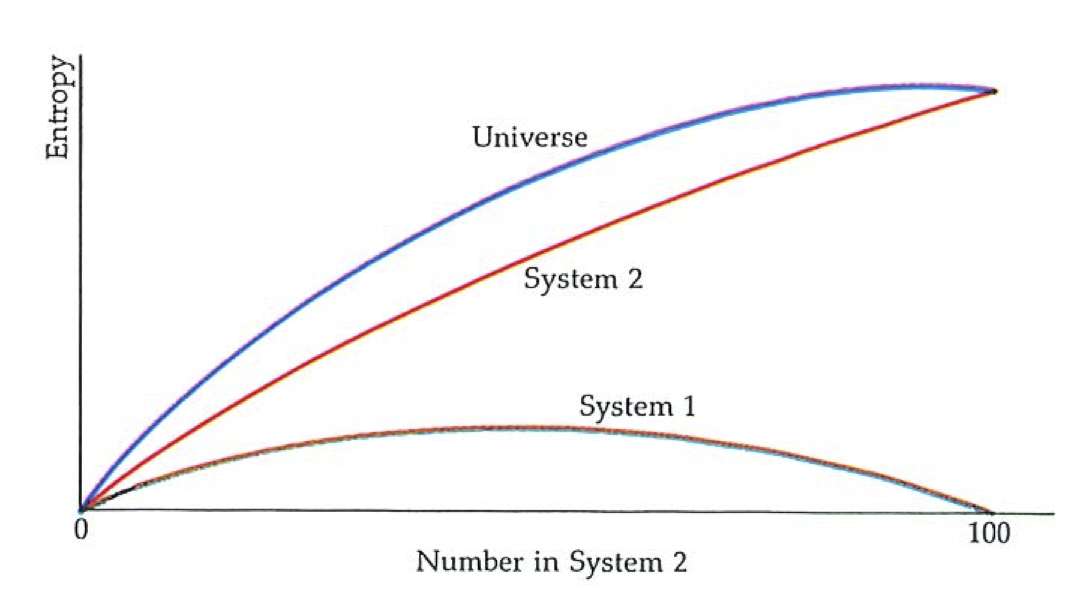
The entropies of System 1, System 2, and the total universe for different numbers of ONs escaped from System 1 into System 2. The entropy of the universe reaches a maximum (of magnitude 369) when the number in System 2 is between 93 and 94 . The temperatures of the two systems are then the same.

The history of the initial state may be pursued into the future using the Entropy program in Appendix 2. The values of the entropy of each system and of the universe (their sum) are shown above. The entropy of System 1 initially rises, because the Demon has more freedom to locate the ONs as soon as gaps are available; but as soon as half the atoms are turned OFF, the entropy begins to fall, because now the Demon is running short of $\mathrm{ONs}$. If all the atoms were to be extinguished, the Demon would be unable to act; so the entropy would again be zero. The entropy of the other system behaves differently: although it is gaining energy, it will never acquire enough to turn one half of its atoms ON (there are only $100\mathrm{ONs}$ initially, whereas System 2 has 1,500 atoms). Therefore the entropy of System 2 only rises. The entropy of the universe as a whole therefore goes through a maximum.

From the graph we see that the maximum of the universe’s entropy occurs when the proportion of atoms ON to OFF in System 1 is the same as that in System 2, that is, when their temperatures are the same. This is exactly what we expect the entropy to signify. We have seen intuitively that energy will disperse, and we know that this dispersal must correspond to the increase of the universe’s entropy. Now we have seen that Boltzmann’s epitaph captures both wings of description: “energy tends to disperse” is equivalent to saying that “entropy tends to increase.

An initial state of the Mark I universe in which 99 atoms are $\mathrm{ON}$ in System 2 and only 1 is ON in System 1.

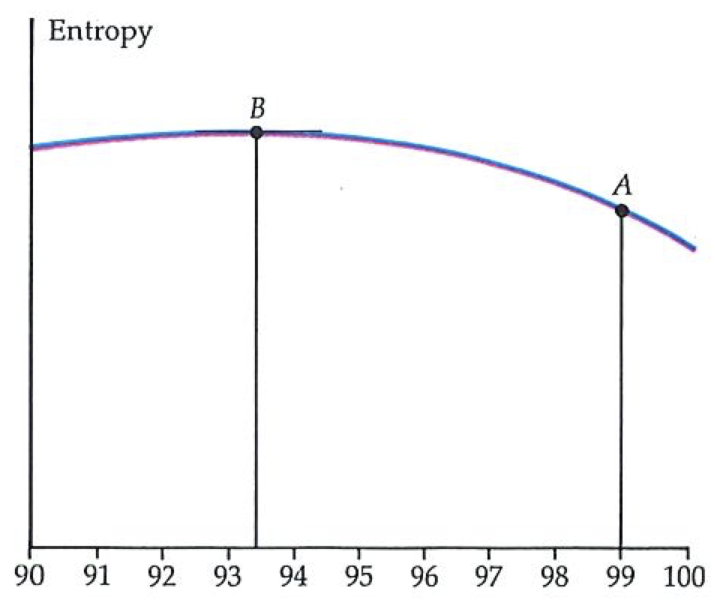
The entropy of the Mark I universe shown in the figure at the top of the page, with increasing numbers of atoms $OFF$ in System 2 (and $ON$ in System 1). The initial state (in the figure at the top of the page) corresponds to the point marked A: the maximum entropy is reached at B. At B the two systems are in thermal equilibrium, and their temperatures are the same (apart from fluctuations).

Notice too how the illustration at the top of the facing page lets us account for the natural direction of energy flow in a temperature gradient. Suppose we have an initial arrangement of the universe in which only one atom of System 1 is $\mathrm{ON}$, and 99 atoms of System 2 are $\mathrm{ON}$. Then we know from our earlier remarks that the temperature of System 1 is lower than that of System 2 (the temperatures are respectively $0.22$ and $0.38$ if we use the formula given on page 56). The entropy of the universe is therefore at the point marked $A$ in the figure on the left. Intuitively we know what will happen: the energy of System 2 will jostle into System 1 until it is uniformly distributed over the entire available universe (see the figure on the next page). This corresponds to each of the 1,600 atoms having an equal likelihood of being ON: since there are $100\mathrm{ONs}$ overall, at equilibrium we can predict that the chance of any one being $\mathrm{ON}$ is $100/1,600$, or $0.0625$, whether the atom belongs to System 1 or to System 2. Since there are 100 atoms in System 1, the number of its atoms $\mathrm{ON}$ at equilibrium is $100\times$ $0.0625=6.25$. However, that number must be an integer because atoms are only fully ON or OFF; therefore the number must be fluctuating around 6 and 7; for simplicity we take it to be 6 (or occasionally 7). The other 94 (or 93) $\mathrm{ON}$ atoms are therefore all in System 2.

When 6 (or 7) atoms are $\mathrm{ON}$ in System 1, the temperature is $0.36(0.39)$; when 94 atoms are $\mathrm{ON}$ in System 2, its temperature is $0.37$ (it is also $0.37$ when 93 are on, because in the bigger system the temperature is less sensitive to numbers). These temperatures are virtually the same (the difference arises from the fact that we have rounded $6.25$ to 6 or 7 ). Not only are the temperatures the same, but they correspond (as we can see from the figure to the left) to the maximum value of the entropy of the universe, point $B$, exactly as our earlier discussion requires: the cooling to thermal equilibrium corresponds to an increase toward maximum entropy.

One distribution of ONs corresponding to thermal equilibrium between Systems 1 and 2, and to point B on the entropy curve.

The Demon’s Cage

Each successful quantitative step of science brings in its wake new qualitative insight. The progress of science can often be traced to a symbiosis of insight and mathematics: each one eases the other along, and as progress is made so comprehension flourishes. The same is true of the step we have now taken: the step, from the intuitive notion of chaos to its precise formulation in terms of the number of arrangements open to a system but invisible to an external observer.

The new insight obtained from Boltzmann’s tomb concerns the nature of equilibrium. In the model we have been considering, the maximum entropy of the universe occurs when the two systems are at thermal equilibrium. Then there is no net flow of energy from one to the other, and there the two systems will remain forever, except for chance fluctuations that happen, very occasionally, to ripple the evenness of the distribution. At thermal equilibrium the systems appear to be at rest, and net change is quenched. But in fact the Demon is as active as ever. Boltzmann’s Demon never dies; it scurries furiously and randomly from atom to atom, extinguishing here and igniting there. Thermal equilibrium is an example of dynamic equilibrium, where the underlying motion continues unabated and the externally perceived quiet is an illusion. Almost all the final resting conditions of the processes that we shall consider are dynamic equilibria of this kind, and we shall see many examples of atomic life continuing after the bulk seems dead.

But there is an even more important point. Dynamic equilibrium represents the Demon caught in the cage of its own spinning. Thermal equilibrium, as we have seen, corresponds to the condition of maximum universal entropy. It therefore also corresponds to the thermodynamic (average) state that can be achieved in the maximum number of ways. If we think of the universe as being able to exist with many arrangements of ONs scattered over either system, then different scatterings may correspond to different thermodynamic states; but in general many different scatterings of ONs will correspond to each state. We can then ascribe a probability to each thermodynamic state in terms of the number of ways in which, at a microscopic level, it can be achieved. Then the more ways in which a state can be achieved, the higher its probability, in the sense that a chance scattering of $\mathrm{ONs}$ is more likely to land in an arrangement corresponding to a given thermodynamic state if that state can be achieved in many ways. In this most ways) is the most probable state of the universe. In other words, thermal equilibrium corresponds to the most probable state of the universe.

This conclusion can be expressed in a slightly different way. We allow the Demon perfect freedom to shift and change; therefore, in due course, it runs through all the possible arrangements of $100\mathrm{ON}$-nesses (and may enter many arrangements many times). We may have to wait a trillion years, but the time will come when every configuration of the universe will have been achieved. However, almost all the arrangements correspond to a uniform distribution of $\mathrm{ON}$-ness; perhaps for a millisecond in those trillion years the universe will be found with all the atoms of System 1 turned $ON$, but for most of the time the energy will be almost uniform. This is because there are so many arrangements that correspond to uniformity (but which its time generating them, and for only a miniscule fraction of its time does its time generating them, and for only a miniscule fraction of its time does it happen to achieve others.

This point can be explored by using the Fluctuation program in Appendix 3. Of course, with a universe of only 1,600 atoms and with System 1 being as small as 100 atoms, the chance that significant abnormalities will be stumbled into by the Demon is quite large. Nevertheless, if the program is run, it will be found that substantial fluctuations occur only infrequently, and most of the Demon’s labors are imperceptible. As an example of this kind of behavior, the figures on the next two pages show several frames in succession: all of them correspond to having six or so atoms $\mathrm{ON}$ in System 1. Even though the atoms that are $\mathrm{ON}$ are different in each frame, we of the blunted thermodynamic eye cannot perceive that. We regard the system as being in a steady state: the thermometer remains steady while the Demon deploys.

Some more of the myriads of arrangements of ONs at thermal equilibritm. Most of the time there are 6 or 7 atoms $ON$ in System 1.

This feature of change is exceedingly important. There are many states of the universe, and the random wandering of the energy permits them all, in principle, to be achieved. A fragment of the universe might begin in a highly improbable state (for example, in the arrangement shown in the top figure on page 71, in which System 1 is relatively cold). After that we shall see the universe drifting through ever more-probable states. That is the natural direction of spontaneous change. When the universe arrives at a more probable state (that is, one that can be achieved in more ways), it almost certainly does not return to a less probable one, because the likelihood of random jostling taking it there by chance is too remote. The final condition of equilibrium of the universe is then its most probable state. The Demon has spun its own cage: the very chaos with which it acts ensures that it is trapped in the future and cannot return to the past. It could return to the past by unraveling chaos if it acted purposefully; but it acts at random, and chaos cannot undo chaos except by chance.

Such are the properties of the model universe. The properties of our actual Universe mirror them precisely, but its energy can be dispersed in so many ways that extraordinary structures may emerge and appear stable as the Universe sinks virtually irreversibly toward equilibrium. However, we have now discovered the essentially statistical way in which systems evolve. We see that the irreversibility of natural change results not from certainty, but from probability: perceived events correspond to the evolution of the Universe through successive states of increasing (and, once attained, overwhelming) probability. In principle, therefore, the Universe has loopholes for miracles.

It would be regarded as a minor miracle, for instance, if a lump of metal were suddenly spontaneously to glow red hot, let alone if water were spontaneously to turn into wine. But the Demon might succeed in bringing about at least the lesser miracle, and could do so by chance. It is conceivable, because the probability is not absolutely zero, that the aimless actions of the Demon could accumulate a great deal of energy in a tiny region of the Universe. But the probability of that happening is negligible, and the probability that the fundamental particles of water might stumble into an arrangement that we would recognize as wine is even more remotely infinitesimal. The loophole exists, but it is almost infinitely small, and the greater probability is that the reports of miracles are exaggerations, falsely reported rumors, hallucinations, deceptions, misunderstandings, or simply tricks. To paraphrase David Hume: it is always more probable that the reporter is a deceiver than that the miracle in fact occurred.

Chaos, Coherence, and Corruption

The relation of the entropy to $W$ as expressed by the Boltzmann equation sharpens the meaning of chaos. We shall do two things with it. First, we shall express more precisely what happens in the course of natural change. Then we shall use it to encompass the disorder in the way that matter is arranged

The natural direction of change is from coherently stored energy (upper illustration) to incoherently stored energy (lower illustration).

Consider what is involved in the chaotic disruption of coherence, as when the ordered motion of a body (see figure on left) gives way to thermal motion (as we discussed for the bouncing ball). The entropy of the initial state of the body is zero, because all the atoms are moving coherently. In terms of the activities of the Demon, there is no way in which it can rearrange the ${\mathrm{ON}}^{\ast }$-ness, for any change would alter the state of motion of the body, which we would detect. Hence Boltzmann’s $W$ is equal to unity, and his equation gives an entropy of zero. The body might be warm, in which case it would possess an entropy, but that would merely add a thermal contribution to the total; for simplicity we shall suppose the temperature to be zero, and therefore that there is no entropy from this source. The table that the body is about to strike is also perfectly cold, or so for simplicity we may suppose.

When the perfectly cold body strikes the perfectly cold table, energy is dissipated into the thermal motion of the atoms of both. The entropy of the table and the body therefore both rise, because now the Demon has ONs to deploy. Overall, therefore, there has been an increase of entropy.

The universe is shifting toward a state of higher probability. Initially there is only one arrangement for the ON-ness of the atoms (and indeed they have to be not merely $\mathrm{ON}$ but ${\mathrm{ON}}^{\ast }$ in a definite direction). This coherent motion of correlated excitation would be a very improbable outcome if the Demon were simply handed a bag of ONs and were left to deploy them. On the other hand, each successive bounce leaves the universe in a more probable arrangement, one that the Demon is more likely to achieve. In the end, when the energy is uniformly and incoherently distributed, the universe is in its most probable state, the state in which the Demon can spin arrangements almost forever without detection.

Now we take the last step toward the complete identification of chaos. Suppose that the particles of the universe are free to move, and that they, as well as their energy, can move from place to place, as they could if the universe were a gas. Suppose we prepare an initial state by injecting a puff of gas into one corner of the universe (upper figure on right). We know intuitively what will happen: the cloud of particles will spontaneously spread and in due course fill the container.

That behavior is easy to understand in terms of the onset of chaos. A gas is a cloud of randomly moving particles (the name “gas” is, in fact, derived from the same root as “chaos”). The particles are dashing in all directions, colliding, and bouncing off whatever they strike. The motion and the collisions quickly disperse the cloud, and before long it is uniformly distributed over the available space (lower figure on right). There is now only an extremely remote chance that the particles will ever again simultaneously and spontaneously accumulate back in their original corner. Of course, we could drive them back into the corner with a piston, but that would involve doing work, and the accumulation would not have been spontaneous.

An initial stage of the Mark I universe is prepared by squirting in a puff of gas (yellow atoms) into one corner.

The equilibrium state of the wniverse consists of particles of gas dispersed uniformly (on average) over the available space. This shows just one such arrangement; there are myriads more. This state of the universe can be achieved in many more ways than the initial state; so the universe is in a more probable state.

Clearly, the idea that energy tends to disperse accounts for the change we have just described, for now the ON-ness of the atoms has been physically dispersed as the atoms themselves spread. Each atom carries kinetic energy, and the spreading of the atoms spreads the energy. But in what sense has the entropy increased? We can get the answer from the Boltzmann expression by thinking in terms of the value of $W$ and the activity of the imperceptible Demon.

An initial state of the turiverse in which all 800 particles of gas lie in the left half of the container.

Suppose the initial cloud occupies one-half of the entire universe, as in the figure above. We know, from experience, that in a final equilibrium state the gas will be spread throughout the universe (as in the figure on the facing page), and therefore occupy twice the original volume. In the initial state the Demon’s domain is only on the left, and then we know that some particle $A$ must be there. In the final state the Demon can deploy the atoms (which, for convenience, we shall regard as all being equally $\mathrm{ON}$ ) in either half of the universe. Atom $A$ now may be either on the left or on the right. So long as there are compensating shifts of other particles, as the Demon (now disguised as the chance collisions) moves the atoms from place to place, the external observer is unaware that the inner structure of the gas is a tumultuous storm.

The equilibrium state of the gas, where the particles are distributed uniformly. Nowo any particle is equally likely to be found in the right half or the left half of the container. The entropy of this state is greater than the initial state by 800 $\ln 2$.

For each particle, the number of locations the Demon can move it to is increased by a factor of 2 when the gas is allowed to spread throughout the entire universe. Consider two particles: when the second is also allowed to explore the entire universe, it too has twice as many possible locations as it had at first. Therefore, in a sample of two atoms the number of arrangements corresponding to the same energy increases when the cloud expands by a factor of $2\times 2=2^2$. For three the increase is a factor of $2\times 2\times$ $2=2^3$, and so it goes on. For a sample of 100 particles the value of $W$ increases by a factor of $2^{100}$. Therefore the Boltzmann equation tells us that the entropy increases from its original $\ln W$ to $\ln (2^{100}\times W)$. The increase is therefore the difference of these two quantities*, or $\ln 2^{100}$. This increase is equal to $100\ln 2$, or 69.3. Hence here also, as we should expect, we have an increase in the entropy of the universe.

• We are using the property of logarithms which tells us that $\log ax-\log x=\log$ $a+\log x-\log x=\log a$. In the next step we use the relation that $\log x^a=a\log$ $x$. The rules are true for logarithms to any base.

The Boltzmann equation therefore captures another aspect of dispersal: the dispersal of the entities that are carrying the energy. In fact his tomb is universal. However energy is dispersed, by spreading from one platform to another, or by the platforms themselves spreading and mingling with other platforms, or by a simple loss of coherence within a sample, it corresponds to the increase of entropy. That is the power of the Boltzmann equation: it enumerates corruption in all its forms.

---

5 THE POTENCY OF CHAOS

This is the turning point of the fortunes of chaos. Our hero, apparently committed to a life of dissipation, degeneration, and general corruption, is about to make good.

On the one hand, we have the world of phenomena: the immediate world of appearance and process. This is symbolized by the steam engine. On the other, we have the world of underlying mechanism. This is symbolized by the atom.

Reflection on experiences with the steam engine identified a dissymmetry in the workings of Nature, which, we found, could be encapsulated in the remark that the entropy of the universe always increases in any natural change. Entropy, we saw, was related to the value of $\mathit{\text{(Heat supplied)/Temperature}}$. We also saw an economic consequence of the dissymmetry: there is an intrinsic inefficiency, a tax to pay, when heat is converted into work. This inefficiency is governed by the temperatures involved in the operation of an engine.

Reflection on the microscopic world of atoms showed that we should expect natural processes to be those in which there is a dispersal of energy. We have refined the meaning of “dispersal”, and have seen that it signifies the spreading of energy, either by the motion of what carries it or by its transfer from one carrier to another. We have also seen that dispersal signifies a loss of coherence in the manner in which energy is stored. We have claimed that all the processes of the world are aspects of this general dispersal, and that spontaneous processes are the manifestation of the purposeless, underlying spreading that chance brings about and that lack of regulation allows.

The bridge between the two worlds is the epitaph on Boltzmann’s tombstone. It relates the entropy, as encountered in the world of experience, to a measure of dispersal, which we can interpret in terms of events in the microscopic world. The Universe, we have seen, is ineluctably drifting through states of ever-increasing probability. Once any new state has been attained (by any natural action), the Universe is locked out of the past, for any turning back is too improbable to be significant.

That is the general background to the events that surround us and take place within us. But Nature has an extraordinary way of slipping into chaos, and sometimes (often, in fact) does so unevenly. The world does not degenerate monotonously. Here and there a constructive act may effloresce, as when a building or an opinion is formed. The descent into universal chaos is not uniform, but more like the choppy surface of xapids. In a local arena there may be an abatement of chaos, but it is an abatement driven by the generation of even more chaos elsewhere.

We now need to unravel the network of connections that Nature drives as it sinks into chaos. We shall begin by returning to the Carnot cycle, newly equipped with our insight into the purposeless behavior of atoms and energy, and see how the corruption of the quality of the energy in the world may bring about local abatements of chaos. Then we shall explore the structural potency of chaos.

Carnot under the Microscope

We can build a simple model of the Carnot engine using the Mark II version of the universe (below). The Mark II universe, remember, is like the Mark I, but the surroundings of the system of interest are infinite: the hot source is an inexhaustible supply of energy, and the cold sink is an insatiable absorber of energy. The indicator diagram for the Carnot cycle we described in Chapter 1 is reproduced above, right. What we now have to establish is how the random dispersal of energy succeeds in producing coherent motion: we have to establish at a microscopic level how heat is converted into work.

figure page 82

figure page 83

At $A$, at the start of the cycle, the working gas is at the temperature of the hot source. That is, the ratio of the number of $\mathrm{ON}$ atoms and OFF atoms is the same in both. (We are taking the simplistic view that the energy needed to turn an atom $\mathrm{ON}$ is the same in the surroundings as in the working substance.) From now on we shall say simply, “The ON:OFF ratio is the same.” The atoms of the gas are free to move and collide with anything that happens to lie in their path.

All the walls except one are rigidly fixed in place. The exception is the piston. The crucial feature of the engine is that it possesses at least one wall that can move in response to the impacts it receives. Here is an essential asymmetry of the engine: it possesses a directional response to the impacts it receives. The face of the piston is, in effect, a screen: it picks out and responds to the motion of particles that happen to be traveling perpendicular to it; and it rejects (by not responding to) components of motion that happen to be parallel to it. Engines, in effect, select certain motions of the particles within them. The directionality of the movement of an actual piston in an engine is a consequence of this asymmetry. Our exploitation of heat to achieve work is based on the discovery that the randomness of thermal motion can be screened and sorted by asymmetry of response.

The random thermal motion of the particles of gas is transformed into coherent motion of the particles that constitute the piston (and then of whatever the piston is rigidly attached to). As a result, some of the particles are switched OFF, because they have jostled away their motion (see the top figure on the next page). However, since the gas remains in contact with the hot source as the piston moves back, and since energy continues to

missing page 84!!!

figure page 85

At $C$ the turning of the crank reverses the direction of motion of the piston, and thermal contact is established with the cold sink (above). Now the coherent motion of the incoming piston stimulates the particles to move more rapidly as they collide with it (just as ping-pong balls go faster after being hit by the paddle: compression is just a vast, simultaneous game of ping-pong). Thus work is being done on the gas, because energy is being transferred to it by the coherent motion of the particles of the piston. This coherent motion is picked up by the particles of gas. However, the particles collide among themselves so rapidly that in fractions of a second the motion has been rendered incoherent. Although work is being done, the coherence of the motion is dissipated so quickly that it results in incoherence. The gas, however, although it is increasingly turned $\mathrm{ON}$, does not get hotter: the jostling of the atoms among themselves and with the walls ensures that the gas remains at the same temperature as the cold sink with which it is now in contact.

At $D$ the thermal contact with the sink is broken, and the compression becomes adiabatic. The particles of the piston continue to stimulate the motion of the particles of the gas, and more and more of these turn ON (see figure on the next page). Now they cannot jostle their energy to the surroundings; so the work done by the incoming piston raises the temperature of the gas. This brings us to $A$, and the cycle is complete.

figure page 86

In the course of completing the cycle, more disorder than order has been created. The coherent raising of the weight to which the piston is attached is a process perfectly free of entropy production (so long as it is quasistatic). We draw energy from the hot source. That reduces its disorder, for with fewer atoms $\mathrm{ON}$, the Demon has less scope for rearrangement. Less energy is dumped into the cold sink, but so long as it is cold enough (so that the ON:OFF ratio is low), the Demon lurking there will gain more opportunities to deploy ONs than the Demon in the hot source loses. That is, even a small supply of energy to a cold sink can generate a lot of chaos (a sneeze in a library has more impact than a sneeze in a crowded street). Therefore, provided some atoms are turned $\mathrm{ON}$ in the cold sink (and the appropriate number depends on the proportion already ON, that is, on the temperature there), we may be able to produce more disorder in the world than we had originally, even though we have eliminated some disorder from the hot source by withdrawing some energy as heat. Consequently, the running of the engine, and its production of work from heat, is a spontaneous, natural process, and the engine will run forward.

This can be expressed differently. The state of the universe at the end of the cycle is more probable than its initial state (in the sense of Chapter 4 since it can be achieved in more ways). Hence the universe enters the new state spontaneously, and then remains there. Entering this more probable state has resulted in a weight being lifted. The raised weight represents the local abatement of chaos, but it has been raised because chaos has been produced elsewhere.

The cycle may be complete, but the world is no longer the same. Energy has wandered out of the hot reservoir and into the cold, but some of it has raised a weight. The shaft of the engine may have raised bricks, blocks, and girders, and from them may have emerged great cathedrals to either gods or mammon. Yet notice how they have been built. They have been built by destruction.

figure page 87

Stirling’s Engine

The Carnot engine is an abstract design. One reason why it cannot be used to build a practical machine is apparent from the illustration on page 83: the area bounded by the cycle is very small. Although the cycle is efficient (if gone through quasistatically), each rotation of the crank delivers very little work. In the remainder of this chapter, we shall examine some of the cycles that are used commercially: we shall see that each is driven by the generation of chaos, even though ostensibly each is driven by the consumption of fuel. Our trucks, automobiles, and jet airliners are all impelled by corruption.

Robert Stirling was a minister of the church and active during the opening years of the nineteenth century, when people were being killed or maimed by explosions that resulted from the use of increasingly higher steam pressure in engines. The ambitions of the engineers outstripped the capabilities of the metallurgists, as they sought to confine high pressure within the inadequate steels of the time. As befitted his calling, he grieved over such personal tragedy, and was to devise an engine that would work at lower, less-dangerous pressures. The Stirling engine remained largely forgotten (like his sermons); but recently it has come of age, for it can be pollution-free, self-contained, and quiet, and has been found especially suitable for refrigeration (when run in reverse).

figure page 88

The principle of the Stirling engine is illustrated below. It consists of two cylinders, each fitted with a piston, and a special device called a regenerator (Stirling, a Scot, called it an economiser) in the pipe that joins them. The two pistons are connected to a shaft, but in a way so subtle that it long defeated the practical implementation of his design. The aim of the connection is to coordinate a complicated sequence of motions of the two pistons, as we shall shortly describe. One of the cylinders is kept hot by a burning fuel or an electric heater. The other is kept cool by cooling vanes or the flow of water. In the model of the engine in the universe (above), one cylinder is permanently in contact with the inexhaustible hot source, and the other is in touch permanently with the insatiable cold.

figure page 89

The regenerator is the special feature of the engine. It consists of a collection of vanes of metal or a pad of wire wool. It has two features. First, it must not be too good a thermal conductor, because it stands between the hot and cold regions of the engine, and the temperature difference must be maintained. Second, it must act as a temporary reservoir, able to absorb heat as hot gas flows through it, and able to give up that heat as cold gas flows through it later. This is its regenerative function: to reheat the cold gas, and to recool the hot.

Initially the engine has its pistons arranged as in the figure at the top of page 90. The piston in the cold cylinder (henceforth piston${}_{\text{COLD}}$) is fully inserted, and the piston in the hot cylinder (piston${}_{\text{HOT}}$) is half-way out.Piston${}_{\text{HOT}}$ moves out while piston${}_{\text{COLD}}$ stays still. This is the power stroke: the crank is turned, and energy floods in as heat from the hot source, exactly as we have already seen in the Carnot engine. This can be represented in the model universe as depicted in the figure. The step takes us to $B$. Since the volume of the gas has increased, but its temperature has remained the same, its pressure declines. This is shown in the indicator diagram at the bottom of page 90.

figure page 90

At $B$ the linkage between the pistons is such that, as piston HOT moves in, piston${}_{\text{COLD}}$ moves out (figure at upper right). This preserves the total volume of the gas as it is shipped from one cylinder to the other. But it is hot gas; so as it flows from one cylinder to the other, it heats the regenerator; the gas’s $\mathrm{ON}$ atoms jostle the atoms of the temporary reservoir. This cooling of the gas at constant volume decreases its pressure, which brings us to $C$ in the indicator diagram below.

At C Stirling’s clever linkage between the motions of the piston keeps piston ${}_{\mathrm{HOT}}$ stationary as piston${}_{\text{COLD}}$ moves in (figure at lower right). This compresses the gas; but the gas’s temperature does not increase, because the piston is connected to the cold sink. Energy jostles out, and the pressure of the gas rises isothermally. This takes us to $D$. Notice that we have shipped heat from a hot source to a cold sink.

figure page 90

figure page 91 double

figure page 92 double

The fourth leg completes the cycle. In order to bring the cycle from $D$ to $A$, piston${}_{\text{HOT}}$ moves out, and piston${}_{\text{COLD}}$ moves in (see below). This maintains a constant volume of the gas (hence the line on the indicator diagram is vertical), and ships it from its cold cylinder into the hot one. As the gas passes through the regenerator, it is heated by the energy previously stored there, and thus simultaneously cools the regenerator back to its initial condition. Now we are back to $A$ : the regenerator is once more ready to absorb heat, and the cycle can begin again.

figure page 93

The Stirling and Carnot engines are similar in that each one works by drawing high-quality energy from a hot supply and dumping it into a cold sink: work is achieved at the expense of the corruption of energy. Furthermore, the thermodynamic efficiencies of the engines are the same: if each is working perfectly, and the cycle is gone through quasistatically, the quantity of energy that has to be discarded in order just to avoid creating more order in the Universe is exactly the same in each engine. Therefore the efficiency of the Stirling engine is given by the expression derived for the $1-{\mathit{\text{Temperature}}}_{\text{COLD}}/{\mathit{\text{Temperature}}}_{\text{HOT}}$.

There is, however, a difference between the two engines: a larger area is enclosed by the cycle in the indicator diagram for the Stirling engine than for the Carnot engine. The larger area means that each cycle in the Stirling engine delivers more work (it has also to absorb more heat; so the efficiency criterion is not contravened). Therefore the Stirling cycle is more suitable for practical applications than the Carnot cycle, because each turn of the crank is more productive.

Productive it may be, but cumbersome it most certainly was, and the first Stirling engines were pretty useless affairs: the linkages between the pistons impaired the efficiency by friction, and the regenerator was far from ideal in its operation. Nevertheless, an engine that can run quietly on any fuel (including sunshine) has obvious advantages. Modern engineering has made the Stirling engine practicable: Stirling engines are now available that can generate 5,000 horsepower. Furthermore, because the Stirling engine works by external combustion, the fuel can be burnt completely, and there are fewer polluting emissions.

A typical design might be something like that shown to the left, and the corresponding actual indicator diagram is shown below: it differs from the ideal cycle we have been considering, but its parentage is clear. The entire engine, including the crankcase, must be sealed. One problem with this engine is that what seems to be sealed to human perception is not necessarily sealed to atoms. Hydrogen could be burned in a Stirling engine; but under the high pressures often used, it diffuses through the “solid” metal walls, and must be replaced continuously. It therefore cannot be used in real applications, even though it is an excellent working fluid, with such low viscosity that it undergoes little frictional loss (the Second Law again) as it is shipped back and forth between the cylinders. However, helium’s viscosity is comparable to hydrogen’s, and is the working fluid used in space-flight applications. In space, the hot source is fospace on the shady side of the craft. The work generated by solar energy in space on the shady side of the craft. The work generated by solar energy in this way is used to drive a generator.

figure page 93

Internal Combustion

The Stirling engine had received little attention until recently because there was an easier way to design small, fairly efficient, compact engines appropriate for mobile applications, first for the automobile, then later for flight. The internal-combustion engine took the world by storm. We shall now see how we literally ride on chaos, for the internal-combustion engines of Otto and Diesel are driven by the collapse of energy into incoherence, and abide by the Second Law.

We shall look briefly at both the Otto engine, the basis of the gasoline powered internal-combustion engine, and the Diesel engine. With neither shall we go into all the technicalities of real engines. Instead, we shall stick to simplified cycles, called the air-standard cycles, in which we pretend that the working fluid is air, rather than the awesome mess of gases that actually comes and goes inside a real engine. This will be enough to show the engines going through their paces, and to reveal the principles of their operation.

The cycle for a four-stroke gasoline engine was first proposed by Beau de Rochas in 1862. It is called the Otto cycle, because Otto succeeded in making an engine that worked (see below). The actual sequence of steps is shown schematically on the facing page, and the model of the engine in the universe is shown on page 96 . The labels $A,B,\dots$ denote the same stages in each illustration.

In the first stage, starting at $A$, a mixture of air and vaporized fuel is sucked into the cylinder as the piston moves out. This occurs at constant atmospheric pressure (except in unconventional engines), and is represented by the horizontal line running from $A$ to $B$ in the figure below.

figure page 94

In the next stage, the mixture of air and fuel is compressed as the piston moves in. This step is supposed to be adiabatic, which is a fair approximation to reality; so more and more of the particles in the cylinder are turned $\mathrm{ON}$ as their thermal motion is stimulated by the incoming piston. If we want to get as much work as possible from the engine, the pressure should be raised as much as possible (so that the indicator diagram gets as fat as possible). However, since the temperature rises also, there is a danger that the fuel will ignite too soon, which would raise the pressure even more, and we would have to push the vehicle (that is, do work on the engine) in order to drive the piston all the way in. For this reason, compression ratios are limited in practice to around 9 or 10.

figure page 95

At $C$, the end of the compression stroke, a spark ignites the mixture; its temperature rises as energy pours into the thermal motion of the particles. This energy is released from the chemical bonds that hold the molecules of gasoline together. Many particles are therefore suddenly turned ON: the fuel is burning. The piston is stationary during this rapid ignition: so the pressure rises as the rapidly moving particles strike the walls. This takes the engine to the condition $D$ in the illustrations.

Now the crank has turned to the point at which the piston starts to move out. This expansion stage, the power stroke of the engine, is supposed to be adiabatic. That is, the particles thumping against the walls give up their energy to the coherent motion of the atoms of the piston (which can respond by moving) and progressively turn OFF, because their thermal motion is not stoked up again by a supply of energy from outside.

figure page 96 complete

figure page 97 complete

At $E$ the exhaust valve opens, and the pressure and temperature drop to their atmospheric values (or whatever the local conditions happen to be). At this stage heat is being dumped, as the Second Law demands, into the metal of the engine block (and whatever cooling system it possesses). The exhaust valve takes the brunt of the thermal stress, and is the primary depository of the heat discarded to meet the demands of the Second Law. The valve is the thermal pivot of the engine. Finally, at $F$, the piston moves in, and dumps the cool, atmospheric gases into the street.

At each stage of the Otto cycle, chaos has been the driving force. Energy has tumbled out of chemical bonds; energy has wandered out into the engine block; and the fruits of combustion, such as they are, have dispersed chaotically into the external world. Though coherent motion has been extracted from the engine (and the atoms of the vehicle and its passengers have moved coherently forward), that coherence has arisen from the generation of chaos.

The Diesel cycle, proposed by Rudolph Diesel in the hope of achieving motive power from the combustion of powdered coal, is quite similar to the Otto cycle, but differs from it in several important ways. We can follow it through the schematic representation of the engine (below), the indicator diagram on page 98 , and the universe model on page 99.

The advantage, in principle, of the Diesel over the Otto engine is apparent from the first stage of the cycle. The retraction of the piston (from $A$ to $B$ ) sucks in air alone, not an air-fuel mixture. The adiabatic compression can therefore take place up to high pressures, and therefore up to high temperatures, because there is no fear that the gas will explode. Only at $C$ is fuel sprayed in, and the high temperature it encounters (in other words, the large proportion of atoms that are $\mathrm{ON}$ and can bang into its molecules sufficiently vigorously) is enough to ignite it without any electric spark.

figure

In the ideal Diesel cycle, the ignition of the fuel occurs at constant pressure, while the piston is actually moving out; so the temperature rises (because of the combustion of the fuel) at the same time that the volume increases, as the piston is withdrawn. Then, when all the injected shot of fuel is burnt, and while the piston is still moving outward, the temperature and the pressure fall, because now the expansion is adiabatic. At the end of this power stroke, the cycle is at $E$.

figure

At $E$ the exhaust valve opens, and the hot, high-pressure gas inside the engine comes to the same temperature and pressure as the nearby outside world, as atoms and energy jostle into dispersal. Once again the metal of the engine is the immediate sink for the heat: the crucial element in the engine is again the exhaust valve, where the chaos is generated that makes the cycle spontaneous and hence the engine useful. (A truck can be thought of as deriving its motive power from the chaos that its engine generates in its exhaust valve.) Then the piston starts to come in. As it does so, it drives the gases in the piston out into the street. This brings the cycle back to $A$. Not only have we generated a little chaos, but we have also moved the vehicle some way along the street.

figure

There are two points worth making before we leave these two everyday engines. First, we have been describing cycles in four-stroke engines, in which the crank rotates twice in order to achieve one power stroke. The excursions from $A$ to $B$ and from $F$ to $A$ in the two cycles represent one complete turning of the crank, but contribute nothing to the power output of the device: they are shopping and spring-cleaning expeditions. If we can eliminate them, we may be able to improve the efficiency of the engine. In engineering it is a general truth that unnecessary processes are wasteful processes, not merely neutral (the Second Law will always seek out some friction). Greater efficiency may result from eliminating them; however, the actual method we contrive to eliminate them may also result in even more unwanted dissipation.

By eliminating the extra turning of the crank, we arrive at the two-stroke engines, in which a power stroke falls in each revolution. In the two-stroke Diesel engine, for instance, the cycle is that illustrated below: at $B$ air is blown into the cylinder, forcing out the exhaust gases, and replenishing the cylinder with fresh air, readying it for the next cycle. In practice the blower is run from the engine itself. This uses up some of the power output from power stroke in each two-stroke cycle.

The second point concerns another intrinsic inefficiency in the Otto and the Diesel cycles, one that is quite separate from the inerradicable thermodynamic inefficiencies of heat engines. In each cycle the power stroke ends when the piston is at $E$, that is, when the gas inside is hot and under pressure. Step $E$ to $F$ in each cycle merely squanders the high-quality energy stored in the gas, and makes no attempt to withdraw it as work. We know that it is high quality for several reasons, one being that it tumbles out into the world at such high temperatures, and energy stored at high temperature is of excellent quality. In order to take advantage of this highquality energy, we should find some way to use the hot exhaust gas, not merely dump it into the universe.

figure

One way of capturing this quality before it is donated as a free gift to the $ϵ$ xhaust valve (in either kind of engine) is to attach a turbine to the exhaust, and thus lower the gas down to the temperature of the outside world gradually, instead of wastefully squirting it there. A turbine is a device for extracting coherent motion from chaotic motion, just as a reciprocating engine is, but a turbine goes around instead of back and forth; we shall see more of its operation shortly. Turbines are efficient, but normally are limited by the fact that they have to withstand continuous high temperatures rather than the periodic surge of temperature characteristic of a reciprocating engine. However, we are now considering using the relatively low-temperature gases at the tail end of the Otto or Diesel engine; so this problem is not severe. We can therefore take advantage of their intrinsic efficiency without having to trouble about metallurgical problems.

The combination of a reciprocating engine and a rotating engine allows the adiabatic expansion (which originally led from $C$ to $D$ ) to continue to $X$ (see below). This extracts, without too many deleterious losses, more of the energy released by the combustion of the fuel, and is a commercially effective way of increasing the efficiencies of engines. The turbine need not be connected to the direct load that is being driven by the engine-the wheels of the vehicle, for instance-but may be used to blow air into the cylinders and add to their efficiency that way. This is the idea behind the turbo-supercharging of truck and automobile engines.

figure

Turbine Power

We are not all confined to the surface of the Earth: chaos can give us wings. In order to complete this rapid survey of the ways in which we have learned to harness chaos and use it to our advantage, we can consider the turbine, which deserves much more than a passing glance, because it is the heart of much modern power. Turbines are anchored to the Earth to generate electric power, and fly through the air in airplanes.

The operation of a turbine can be idealized by yet another cycle, the Brayton cycle, which is based on the collection of processes shown schematically below. The compressor stage may be driven by a reciprocating engine, but it is more appropriate to think of it as a rotating fan of some kind. We shall start with the closed cycle, in which the same working fluid circulates indefinitely (as in the Carnot and the Stirling engines). Then we shall open the cycle, and allow the engine to take flight.

The closed Brayton cycle runs as follows (see figure on facing page). First, the working fluid is compressed by a turbine, which is driven by bleeding off some work from a later part of the cycle (this bleeding is represented by the line joining the compressor and the turbine in the illustration below). This compression is adiabatic, and it raises both the temperature and the pressure of the gas. It takes the state of the gas from $A$ to $B$. At this stage, $B$, energy is transferred to the high-temperature, high pressure gas (because fuel burns, or because there is some kind of heat exchanger fueled by a hot source). Its temperature then rises still further, but the engine is arranged so that at the same time the volume of the gas is allowed to increase; overall, therefore, it remains at constant pressure. This brings its state to $C$.

figure

figure

At $C$ the hot, expanded gas enters the turbine. That stage is represented in the cycle by the adiabatic expansion from $C$ to $D$, which cools it and extracts its energy as work. This time the work results in the coherent motion of the atoms of the blades of the turbine. Finally, in order to return to $A$ and to close the cycle, we must lower the temperature at constant volume. Here once again, we dump heat into a sink in order to complete the cycle and to achieve a viable engine. The technical difficulty of making this cycle practicable has already been mentioned, but is worth emphasizing: the hot and cold devices are separate; so the turbine must be kept at a high temperature while it is running. Turbines therefore became feasible only after metallurgists had developed materials able to withstand high temperatures for long periods.

We can interpret the Brayton cycle in terms of the behavior of individual particles, much as we have already done for the other cycles. Work is done in the stage from $C$ to $D$, in which the incoherent thermal motion of the hot gas is transformed, at least partially, into the coherent rotational motion of the blades. Likewise, in the compression step, work is done as the rotating blades compress the gas: their coherent motion is passed on to the particles they happen to hit. Almost immediately, the coherent motion of the particles is lost as they collide with each other; so their energy becomes stored as thermal motion. The fact that coherent motion is being delivered from and to rotating blades, not reciprocating pistons, is not a significant difference in principle, but it has profound consequences for the smooth and efficient operation of the engine. The particles do not care whether they are hitting the same surface (a piston) as it moves toward or away from them, or a constantly renewed surface (a turbine with many blades).

The compression stage turns many atoms $\mathrm{ON}$ in the usual way, and also confines them to a smaller volume. Their natural tendency to disperse, magnified by their higher speeds (higher because their energy is stored in the kinetic energy of their motion), is interpreted by the external observer as an increased pressure. Then, as the fuel is burnt, and its released energy jostles out into the gas (or, if the source of heat is external, as the energy jostles in through the thermally conducting walls), the atoms are stimulated to even greater ON-ness. This takes the gas from $B$ to $C$. Now the tendency to disperse plays out its role, and the particles enter the region of anisotropy of mechanical response represented by the turbine. From $C$ to $D$ we see the particles losing their ON-ness, not to a single surface, but to a constant succession of surfaces. This reduces the temperature and the pressure, and the engine comes to $D$. The final stage of the cycle is to relinquish the thermal motion of the gas atoms to their environment, and to reduce the volume as the less-energetic atoms retreat from the constantpressure surroundings.

Now we open the system, and prepare the engine for flight. We replace the circulation of the working gas by an open flow. Now the engine has an input and an output (see below); new fluid is constantly drawn in and old fluid is discharged. This results in the open Brayton cycle, a model of the jet engines used for flight. The cycle remains thermodynamically similar to the one we have already considered: the incoming gas (the air) is still compressed by the compressor (although the passage of the engine through the air also contributes to the compression). Fuel is still burnt in order to raise the temperature and increase the volume occupied by the passing air. The hot gas still does work on the outside world. In an actual engine the extraction of work occurs in two stages, each of which has a turbine (see below). The smaller of them is used to drive the compressor; the larger is the one the external world sees as the device’s muscle. In jet flight, though, the second turbine is conceptual: the gases simply stream out of the back of the engine. This stage corresponds to work, because the impulse of the particles being thrown out of the rear of the engine is imparted to the aircraft as a whole (as any iceskater who has thrown a ball will have experienced too); so all the atoms of the aircraft and its passengers are moved coherently forward.

figure

Toward Coherence

The central theme of our discussion so far is that chaos can be constructive, and that coherence may stem from incoherence. So far we have seen this in a simplistic way: we have seen that so long as a process is occurring in which more chaos is generated than is being destroyed, then the balance of the energy may be withdrawn as coherent motion. We have seen that natural change arises as the Universe slips into, and is trapped in, states of ever-increasing probability. But we have also seen-and this is the crucial point-that the state of greater probability, the state of more chaos, can allow greater coherence locally, so long as greater dissipation has occurred elsewhere.

We have seen something of the devices that meet the demand of the Second Law for a cold sink, but in ways that allow us to extract motive power from the uneven way in which the world sinks into chaos. We have seen modifications of the Carnot cycle that describe, at least in theory, the operations of viable engines. Thus we have seen that coherent motion may emerge from incoherent motion if the devices are complex (remember the figure on page 12, the realization of the Brayton cycle). But mechanical coherence, the coherence of the motion of particles, is only one aspect of structure. We have seen that achieving coherent motion enables us to build cathedrals (instead of merely heating the stones where they lay) and to move passengers and loads. We may suspect that the same kind of extraction of coherence, more elaborately contrived, may permit us to build bodies. This is the next issue we have to explore.