Ariketak

Kualitatiboak

Galderak dira datozen ariketak, horrexegatik izendatu ditut kualitatibo. Bigarren printzipioarekin lotutako kontzeptuak menderatzea eta ondo erabiltzea dute helburu. Askotan, era artifizialean emanda daude, antza, eta halaxe da, hain zuzen ere punturen bat edo beste azpimarratzeko, zehatz izan behar dela adierazteko eta ideiak argi geratzeko. Nabaria izango da asko aldaerak baino ez direla. Honelako galdera teorikoak, normalean, egon daitezke azterketetan, eta aurreko urteetan egindako azterketatxoak dira, gehien bat.

Oso inportantea da ondo irakurtzea eta ariketa oso ona da erantzuna idaztea, eta idatzitako berrirakurtzea eta, askotan, lagungarri gerta daitekeen formularen bat edo beste erabiltzea eta idaztea.

Lehenaren erantzunak jarraian doaz, argi dera dadin nola eman behar diren erantzunak, ariketaren helburuarekin bat etortzeko.

---

Testuingurua

1. ARIKETA

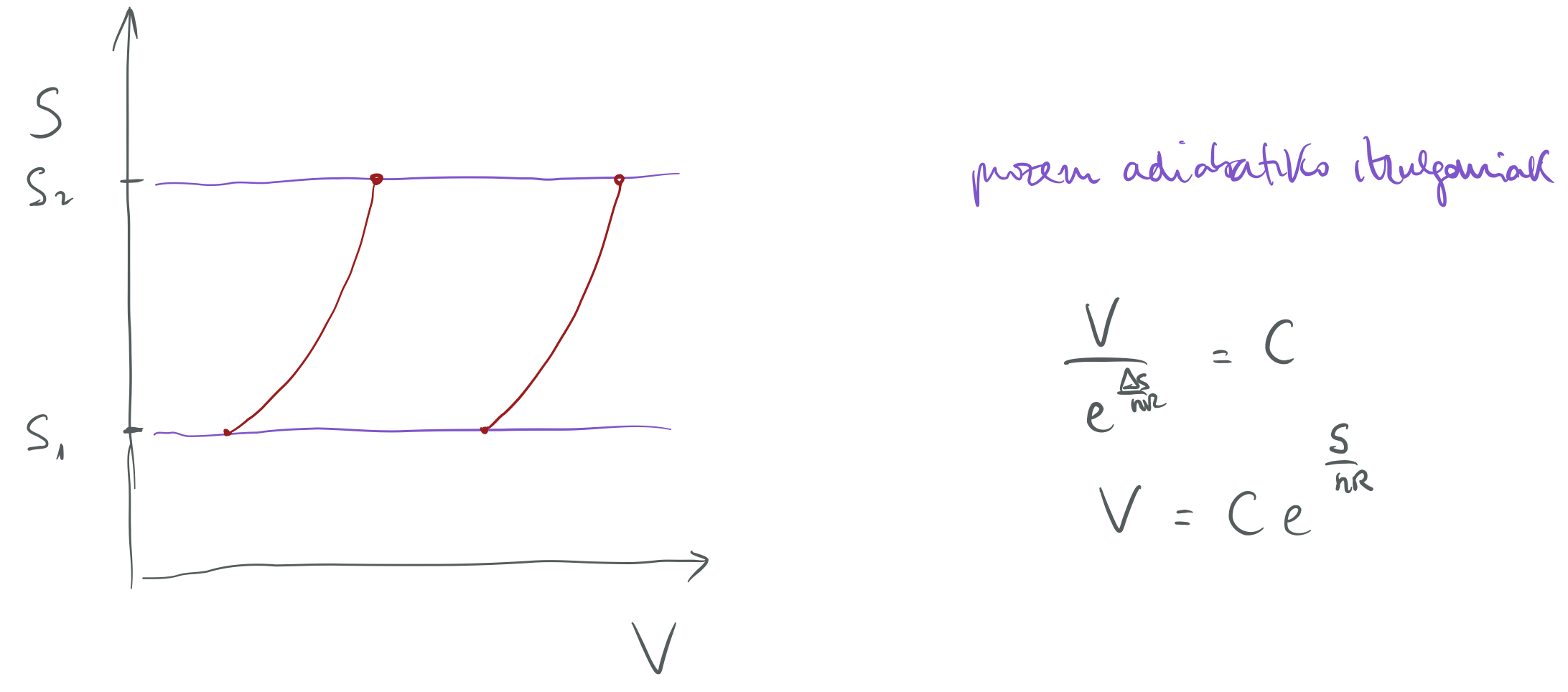
Sistemaren entropia-aldaketa nulua da prozesu adiabatikoetan.

Ebazpen posible bat…

Entropiaren kalkulua tartean dagoenean burura datorkigun adierazpena da entropiaren beraren eragiketa-definizioa, honako hau: $dS=\frac{\delta Q}{T}$.

Baina, adierazpen hori ez da egokia dagoenetan idatzita: derrigorrean prozesuak itzulgarri izan behar du adierazpena erabili ahal izateko, beraz, honako hau da benetan idatzi beharko genukeena (gutxienenez, formalismoz aldatzen ez dugun bitartean…): $dS=\frac{\delta Q_{\text{IG}}}{T}$.

Hori horrela, eta enuntziatuak esan duenez, prozesua adiabatikoa dela, orduan, berehala idazten “dugu” honako hau: $\delta Q_{IG}=0$ (zein itzulezina balitz ere bai, jakina). Hortaz, $dS=0$, eta erantzuna hauxe da (normalean ematen den erantzuna, nahiz eta egokia izan ez): sistemaren entropia-aldaketa nulua da prozesu adiabatikoetan.

Beste alde batetik honako hau ere kontuan hartu behar da: entropia, entropia-funtzioa, batukorra da, askatasun-graduetan (ekarpen bana egiten dute), azpi-sistemetan (sistema konposatuak aztertzen baditugu…azken finean, aurreko kontzeptu berbera da)…

Entropiaren kalkuluaren ikuspuntutik, beti aztertu beharreko sistema unibertsoa da, hots, ingurunea gehi sistema termodinamikoa: biek hartzen dute parte edozein prozesutan, egotekotan behintzat. Hots, sistema termodinamikoak ingurunerik ez badauka, bera da unibertsoa. Enuntziatua berreskuratuz: prozesua adiabatikoa bada, sistemak ez du berorik trukatzen. Beraz, sistemak ez dauka ingurune termikorik, behintzat ikusten duen ingurune termikorik. Hauxe da buruan izateko adierazpena: $\mathrm{\Delta }{S}_U=\mathrm{\Delta }{S}_{sis}+\mathrm{\Delta }{S}_{ing}$. Sistemak ingurunea badauka, termikoa, prozesu adiabatikoa unibertsoan gertatzen da, eta sistemak beroa truka dezake, agian, era itzulgarrian (horrelakorik ez baita aipatzen). Beraz, sistemaren entropia-aldaketak ez du nulu izan behar. Ingurunerik gabeko kasuan eta itzulgarri izanik, bai.

Ideia interesantea hauxe da: entropia aldatzeko modu asko dago. Izan ere, gehienetan, egoera-aldaketak, edozein egoera-aldaketak, entropia-aldaketa dakar, egoera-aldaketa oso berezia ez bada, behintzat, bat zeinean, azpiprozesu infinitesimal orotan (edozein aldiunetan esango genuke, baina ezin dugu denborak ez baitu parterik hartzen…) sistemaren eta ingurunearen entropia-aldaketak elkar konpentsatzen duten, batura nulua eginez. Hori da prozesua (osoa, finitua), itzulgarria izatea, azpiprozesu infinitesimal oro itzulgarri izateak ziurtatzen baitu oreka-egoeren artekoa izango dela eta energia-barreiaketarik gabekoa eta, ondorioz, finitua ere bai. Baina kontuz, unibertsoarenaz ari garelako, bestela ez dago konpentsatzerik.

Demagun aztertu beharreko sistema zilindro adiabatiko batean dugun gas ideala dela eta era kuasi-estatikoan konprimitzen dugula, zilindroa ixten duen marruskadurarik gabeko pistoi adiabatiko idealari esker. Aldatzen al da sistemaren entropia? Trukatu al du sistemak berorik?

Espero dut argi geratu izana, nahiz eta egia izan daitekeen zenbait prozesu adiabatikotan sistemaren entropia-aldaketa nulua izatea, enuntziatuan aipatutakoan eta aipatu den moduagatik hain zuzen ere, zehaztasunik gabe, ezin dela hori erantzun.

*Horren antzera erantzun beharko da…gehienetan…*konturatuko zarenez, esan bezala, beherago dauden enuntziatu batzuk lehenengo honen eta honekin lotutako ideien aldaerak dira.

• Sistemaren entropia-aldaketa positiboa da prozesu adiabatiko itzulezinetan.

• Ingurunearen entropia-aldaketa positiboa da beti prozesu ez adiabatikoetan.

• Lana ezin daiteke oso-osorik bero bihurtu.

• Beroa ezin daiteke oso-osorik lan bihurtu.

---

Testuingurua

2. ARIKETA

• Aztertu honako baieztapenak, eta azaldu, ongi arrazoituz (dena ondo azalduz), egia ala gezurra diren:

• Baldin eta oreka-egoera batean dagoen sistema bati energia kantitate jakin bat ematen bazaio bero eran, sistemak beti lortzen du bukaerako oreka-egoera berbera.

• Ezinezkoa da prozesu isotermo batean lana bero bihurtzea amaigabeko eran.

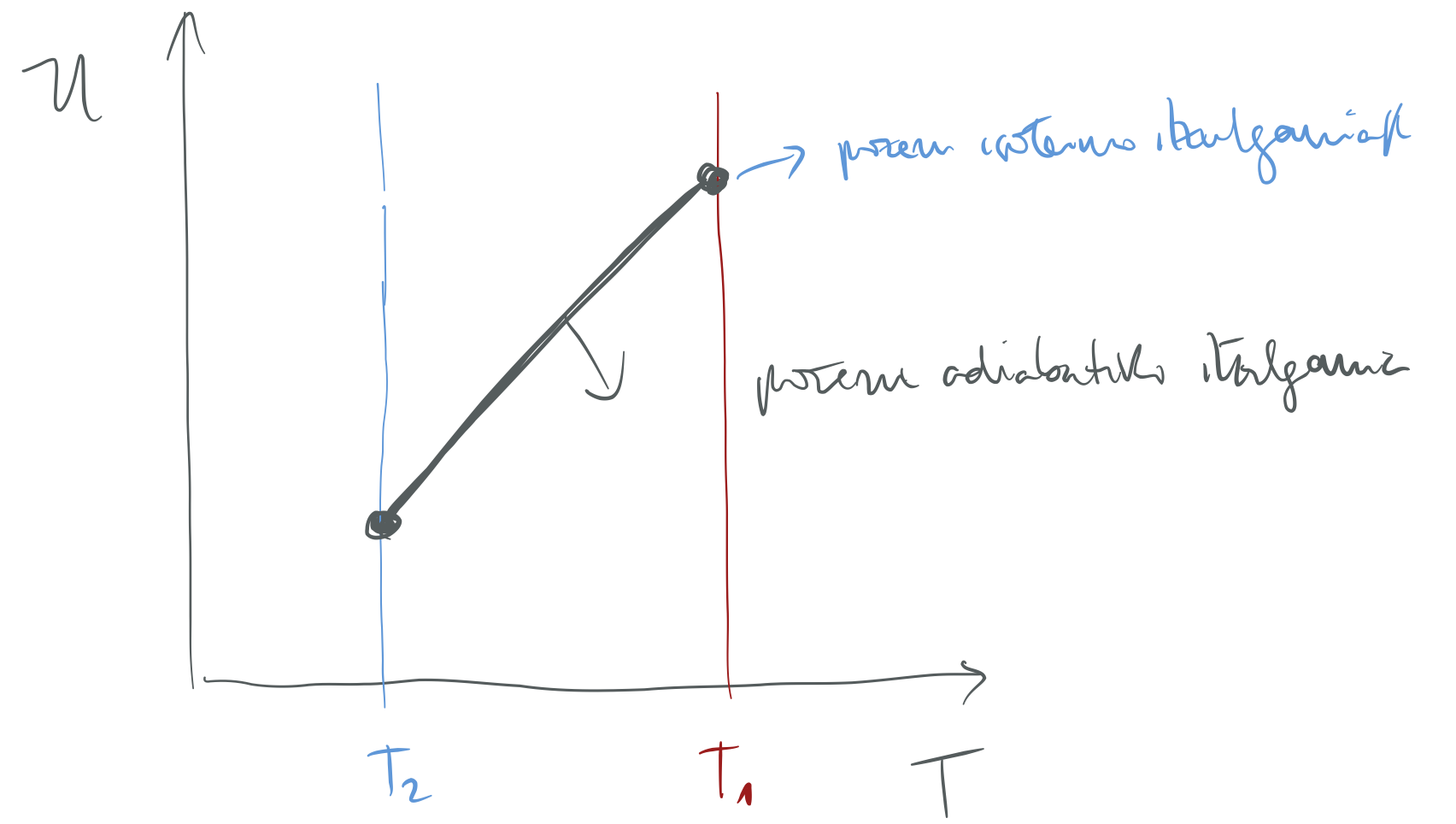
• Prozesu isoentropikoak adiabatikoa dakar ondorioz, eta alderantziz.

• $dS=\frac{1}{T}(C_{V}dT+pdV)$

Ebazpen posible bat…

---

Testuingurua

3. ARIKETA

1. Sistemaren entropia-aldaketa nulua da prozesu adiabatikoetan.

2. Sistemaren entropia-aldaketa positiboa da prozesu adiabatiko itzulezinetan.

3. Ingurunearen entropia-aldaketa positiboa da beti, prozesu ez adiabatikoetan.

4. Lana ezin daiteke oso-osorik bero bihurtu.

5. Beroa ezin daiteke oso-osorik lan bihurtu.

6. Prozesu itzulgarri guztietan sistemaren entropia-aldaketa nulua da.

7. Prozesu adiabatikoari segitu dion sistemaren entropia-aldaketa nulua da.

8. Esku artean dugun sistemaren espantsio askean, tenperaturak konstante iraun du.

9. Esku artean duzun sistemak entropia jaso egingo du beroa xurgatuko badu soilik.

10. Esku artean duzun sistemak zikloa bete du, sistemaren eta ingurunearen entropia-aldaketak nuluak dira beti.

11. Prozesu isoentropikoak adiabatikoa dakar ondorioz. Alderantzizkoa ere egia da.

12. Ba al dago jasotzerik edozein sistemaren entropia beste sistemetan inolako aldaketarik sorrarazi gabe?

13. Itxia den sistemaren kasuan, ez dago barne-loturarik aldatzerik zeinaren ondorioz sistemaren entropia txikiagotuko den.

• Aztergai dugun sistema $A$ egoeran dago. Sistema egon daitekeen $B$ egoeraren entropia A-ri dagokionarena baino handiagoa da. Ondorioz:

• sistema itxia bada, $A$ ezin da $B$-tik lortu

• sistema itxia bada, barne-loturen konbinazioren bat erabiliz, $B$-tik $A$ lortu daiteke

• sistema itxia ez bada, posiblea da $B$-tik $A$ lortzea, egokia den kanpo-sistemaren bat akoplatuz

• aurreko aukera guztiak egokiak dira

• Esku artean dugun sistema $A$ oreka-egoeratik $B$ oreka-egoerara eraman dugu honako prozesu hauetan zehar:

• adiabatiko itzulgarria $+$ isobaro itzulgarria

• isobaro itzulgarria $+$ isotermo itzulgarria

• adiabatiko itzulezina

  Arrazoitu zein prozesutan sistemaren entropia-aldaketa txikiena izan den.

Ebazpen posible bat…

---

Testuingurua

4. ARIKETA

Aintzakotzat hartu ingurunearekin bero kantitaterik trukatu gabe gertatu den prozesua. Ager al daiteke unibertsoaren entropia-aldaketarik? Aipatu bi adibide.

Ebazpen posible bat…

---

Testuingurua

5. ARIKETA

Horma finko, adiabatiko eta iragazkorreko sistemak prozesu itzulezinari segitu dio, zeinak sistemaren entropia txikiagotu duen.

Ebazpen posible bat…

---

Testuingurua

6. ARIKETA

Justifikatu ondoko baieztapenak:

1. Prozesu itzulgarri guztietan sistemaren entropia-aldaketa nulua da.

2. Prozesu adiabatikoari segitu dion sistemaren entropia-aldaketa nulua da.

3. Esku artean dugun sistemaren espantsio askean, tenperaturak konstante iraun du.

Ebazpen posible bat…

---

Motorrak eta hozkailuak

Testuingurua

7. ARIKETA

Gas ideal baten 1 mol-i bolumena bikoiztu dion espantsio isotermo itzulezina eragin diogu. Bero-iturriaren tenperatura 300 K da, eta 3000 joule da prozesuaren ondorioz egindako lana. Aipatutakoa ba al da Entropia-emendioaren printzipioarekin bateragarria?

Emaitza

$\mathrm{\Delta }{S}^{\text{U}}=-0.89\frac{\text{cal}}{\text{K}}$

Ebazpen posible bat…

---

Testuingurua

8. ARIKETA

Posiblea al da Carnot-en makina bat motor termiko moduan dabilenean, bero-iturri berotik 100 joule xurgatzea eta bero-iturri hotzari 600 joule ematea; eta, aldi berean, hozkailu moduan dabilenean, bero-iturri hotzetik 600 joule xurgatzea eta bero-iturri beroan 900 joule uztea?

Emaitza

Ez

Ebazpen posible bat…

---

Testuingurua

9. ARIKETA

Esku artean dugun Carnot-en motorrak bete duen zikloan 100 J hartu du goi-tenperaturan dagoen bero-iturritik; eta 20 J utzi, 200 K-ean dagoen bero-iturrian, behe-tenperaturan dagoenean, hain zuzen ere.

1. Zenbateko presioa erakutsiko du gas-termometroak goi-tenperaturan dagoen bero-iturriarekin ukipenean jarriz gero?

2. Zenbat lan egin behar da hozkailu moduan aritu dadin?

Emaitza

1. Goi-tenperatura $1000\text{ K}$ da.

2. $|W|=80\text{ J}$.

Ebazpen posible bat…

Carnot-en motorra oso motor inportantea da, ez aplikagarritasunagatik, baizik eta teknikoki eta kontzeptualki.

Lehenik eta behin motor itzulgarria da, beraz, hozkailu moduan erabil daiteke baita ere, buelta eman diezaiogulako. Zikloa osatzen lau azpiprozesu dira: bi adiabatiko itzulgarri eta bi isotermiko itzulgarri. Prozesu adiabatikoetan sistemak ez du berori trukatzen; bero-trukea prozesu isotermikoetan gertatzen da. Prozesu isotermikoak direnez, bero-iturriekin ukipen termikoan gertatzen diren prozesuak dira eta bi baino ez daude. Frogatu dugu, motorraren errendimenduak bi tenperaturen funtzioa baino ez dela: berdin dio zer sistema dagoen ziklikoki bueltaka eboluzionatzen, malgukia dela, sistema magnetikoa, elektrikoa, gas ideala…edozein kasutan $T_1$ eta $T_2$ finkatutakoan, errendimendua beti da ${\mu }_C=1-\frac{T_2}{T_1}$ ($T_1>T_2$). Hori frogatu da $T/S$ diagrama erabilita Carnot-en zikloa adierazteko, zeinean zikloaren adierazpena unibertsala den, hots, diagrama horretan ez da sistemari buruzko informaziorik agertzen, zikloari buruzkoa baino ez. Zergatik da hori? Prozesu isotermikoak kanpoko bero-iturriek (inguruneak) finkatzen dituztelako, sistemak berak ezin du ezer egin. Prozesu adiabatikoak, aldiz, sistemaren araberakoak dira, sistemen ezaugarriek (askatasun-graduek) “eramango dute” sistema finkatutako tenperatura batetik bestera (bi noranzkoetan, jakina), era berezian. Baina, hauxe da gakoa: prozesu horiek ez dute parterik hartzen errendimenduaren kalkuluan, horietan berorik trukatzen ez baita (trukatutako beroak erabili behar dira edozein motorraren errendimendua kalkulatzeko ${\mu }_m=\frac{|W|}{|Q\downarrow |}=\frac{|Q_{\downarrow }-Q_{\uparrow }|}{|Q_{\downarrow }|}$). Beraz, modu horretan kentzen ditugu sistemaren ezaugarriak errendimenduaren adierazpenetik: prozesuak itzulgarriak izanik $\delta Q=TdS$ idatz daiteke eta $T$ finkoa denez, isotermikoetan, $Q=T\mathrm{\Delta }S$. Hau da, $S$ eta $T$ dira aldagai naturalak Carnot-en zikloa adierazteko, horixe da ondorioa. Beste edozein diagramatan (lehenik, sistema motaren araberakoa, jakina) prozesu adiabatikoa ($U/T,V/T,\dots$) edo isotermikoa ($S/V$) ez dira aldagai naturalak erabiliz adieraziko eta, beraz, sistemaren ezaugarriak agerraraziko ditugu horien adierazpen grafikoetan. Jakina, errendimenduaren adierazpena inoiz ez da aldatzen: hori frogatuta dago!

---

Testuingurua

10. ARIKETA

Demagun esku artean Carnot-en motorra duzula, zeinean gas ideala dagoen.

1. Adieraz ezazu grafikoki ziklo bakoitzean gasak beteko duen ibilbidea honako diagrama hauetan: $T/S$, $U/T$, $S/V$.

2. Lortu etekina kasu bakoitzean.

Emaitza

Esaterako, $S/V$ diagramaren kasuan, honako hau da adierazpena:

$$V\exp (-\frac{S}{nR})=k$$

Eta, honako hau da adierazpide grafikoa:

irudi-oina

Ebazpen posible bat…

Esaterako, $U/T$ diagramaren kasuan, honako hau da adierazpena:

$$U\propto T$$

Eta, honako hau da adierazpide grafikoa:

irudi-oina

---

Testuingurua

11. ARIKETA

Motor bat 127${}^{\circ }$ C-ko eta 27${}^{\circ }$ C-ko tenperaturetako bero-iturrien artean aritu da. Lehenengo bero-iturritik 3200 J xurgatu du motorrak eta bigarren bero-iturriari 2800 J eman dio. Horrelako motorra existitu al daiteke? Carnot-en motorra al da?

Emaitza

1. ${\eta }_C=0.25$

2. $\eta =0.125$

Ebazpen posible bat…

---

Entropiaren kalkulua

Hurrengo ariketetako helburua da entropia-aldaketa kalkulatzea, zenbait sistematan eta zenbait baldintza esperimentaletan. Hori lortzeko, oraindik eskua artean bi tresna baino ez daukazu (formalismoa aldatu arte): entropiaren eragiketa-definizioa ($dS=\frac{\delta Q_{IG}}{T}$) eta lehenengo printzipioaren adierazpena, $\delta Q=dU-\delta W$ (adierazpen horrek deskribatzen duen prozesua, adierazpena bera eraiki den modua kontuan hartuta, itzulgarria izanik). Hauxe da, beraz, biak aintzakotzat hartuz, eragingarria den tresna bakarra entropia-aldaketa kalkulatzeko:

$$dS=\frac{1}{T}(dU-\delta W)$$

Prozesua itzulgarria bada, prozesua bera erabil daiteke entropia-aldaketa kalkulatzeko.
Prozesua itzulezina bada, ordea, itzulgarri bat erabiliz ordezkatu behar dugu.

Ordezkatzeak esan nahi du eskua sartu behar dela eta unibertsoa, aldatu: dagoeneko aztertuko duguna prozesua ezberdina izango da enuntziatuarekiko alderatuta. Baina, prozesu itzulgarri ordezkari berezia aukeratuko dugu: enuntziatuko hasierako eta bukaerako oreka-egoera berberak lotzen dituena. Besterik ez dugu behar. Entropia existitzen den funtzioa da; matematikoki diferentzial zehatz baten bidez adierazten da, hots, funtzio matematikoa da. Fisikoki, aldagai termodinamikoen funtzioa izango da. Entropiak sistemaren propietate bat adierazten du: badago esatea hauxe da sistemaren entropia. Hortaz, entropia-aldaketak ez dauka prozesua gertatu den ibilbidearekiko mendekotasunik, hasierako eta bukaerako egoeren mendekoa baino ez da haren balioa.

Zer prozesu ordezkari aukeratuko dugu? edozein, gure esku dago; baina, onena da egokiena aukeratzea.

Zein izango da egokiena? Baldintza esperimentalek gomendatzen dutena. Gomendioa guk geuk ondorioztatuko dugu, jakina. Batetik, hasierako eta bukaerako oreka-egoerak ezagututa eta, bestetik, sistemari buruzko informazioa ezagututa, egoera-ekuazioen bidez, gehienetan. Batzuetan, koefiziente esperimentalak ezagut ditzakegu. Horrelako kasuek lan apurtxo bat gehiago exijituko dute. Gogoratu egoera-ekuazioaren deribatuak direla koefiziente esperimentalak, beraz, egoera-ekuazioa berreskuratzeko, integrazio bat egin behar da: horixe da hain zuzen lan gehigarria. Informazio honen guztiaren bidez aukeratuko dugu prozesu ordezkaria eta hori adierazteko egokien diren aldagai termodinamiko independenteak, horien funtzioan lehenengo printzipioaren adierazpen diferentziala idazteko.

Laburbilduz:
Bereizi prozesua itzulgarria ala itzulezina den.

• Itzulgarria denean: prozesua bera erabil daiteke, horretan kalkulatzeko sistemak trukatzen duen beroa

  1. ezaugarritu erabat hasierako eta bukaerako egoerak

  • sistemari buruzko informazioa erabili:

    • egoera-ekuazioak edo

    • koefiziente esperimentalak edo

    • biak…

  2. aukeratu aldagai termodinamiko independente egokiak

  • aurreko urratseko informazioa erabiliz

  • prozesuari buruzko informazioa erabiliz

  3. eraiki $\delta Q=dU-\delta W$

  4. zatitu aurreko adierazpena $T$ erabiliz

  5. integratu hasierako eta bukaerako egoeren artean

• Itzulezina denean: prozesua bera ezin da erabili, horretan kalkulatzeko sistemak trukatzen duen beroa

  1. ezaugarritu erabat hasierako eta bukaerako egoerak

  • sistemari buruzko informazioa erabili:

    • egoera-ekuazioak edo

    • koefiziente esperimentalak edo

    • biak…

  2. aukeratu prozesu itzulgarri ordezkari berezia
     prozesua dagoeneko itzulgarri denez, aurreko atalekoa… 2. aukeratu aldagai termodinamiko independente egokiak

     • aurreko urratseko informazioa erabiliz

     • prozesuari buruzko informazioa erabiliz

     3. eraiki $\delta Q=dU-\delta W$

     4. zatitu aurreko adierazpena $T$ erabiliz

     5. integratu hasierako eta bukaerako egoeren artean

Testuingurua

12. ARIKETA

Aztertu beharreko gas ideala bero-iturriarekin ukipenean dago eta $2p_0$ hasierako presiotik $p_0$ bukaerako presioraino zabaldu da.

Lortu gasaren, bero-iturriaren eta unibertsoaren entropia-aldaketak, honako bi kasu hauetan:

1. espantsioa bat-batekoa bada,

2. espantsio itzulgarrian.

Emaitza

Ebazpen posible bat…

---

Testuingurua

13. ARIKETA

Gas ideal monoatomiko baten $n$ molei konpresio kuasiestatikoa eragin diegu, $m$ masako likidoarekin ukipen diatermoan daudela. Horrela, gasaren tenperatura aldatu da. Likidoaren presioak konstante iraungo du eta bere bero-ahalmena $c_{pl}$ da. Gasaren hasierako eta bukaerako bolumenak $V_A$ eta $V_B$ dira, hurrenez hurren; eta gasaren eta likidoaren hasierako eta bukaerako tenperaturak $T_A$ eta $T_B$. Lortu honako hauek:

1. Likidoak xurgatu duen beroa.

2. Gasaren entropia-aldaketa eta barne-energiaren aldaketa.

3. Gasak egindako lana.

4. Frogatu $A\to B$ prozesuak honako ekuazio honi segitzen diola: $T{V}^{a-1}=C$

5. Lortu $a$ konstantearen balioa eta, berebat, lortu $a$ konstantearen limitea honako bi kasu hauetan:

   • $m{c}_{pl}\to 0$

   • $m{c}_{pl}\to \mathrm{\infty }$

• Zer motatako transformazio izango da prozesua bi muga-kasuetan?

Emaitza

1. $Q^{\text{lik}}=m{C}_p(T_B-T_A)$

2. • $\mathrm{\Delta }{S}^{\text{gi}}=C_V\ln (\frac{T_B}{T_A})+nR\ln (\frac{V_B}{V_A})$

   • $\mathrm{\Delta }{U}^{\text{gi}}=C_V(T_B-T_A)$

3. $W^{\text{gi}}=(C_V+m{C}_p^{\text{l}})\cdot (T_B-T_A)$

4. $a=\frac{nR}{n{C}_V+m{C}_p^{\text{l}}}+1$

Ebazpen posible bat…

irudi-oina

---

Testuingurua

14. ARIKETA

Horma adiabatiko higikorrak bi zatitan banatu du esku artean dugun zilindroa. Zilindroko ezkerreko gunea horma diatermoz inguratuta dago eta eskuinekoa, aldiz, horma adiabatikoz. Gune bakoitzean $C_V$ konstanteko eta ondoko egoera-ekuazioari segitu dion gasaren mol bakarra dago:

$$p(V-b)=RT$$

adierazpen horretan $b$ konstantea da. Hasiera batean, guneetako bi gasen hasierako egoera berbera da: ($p_0$,$T_0$). Ezkerreko guneari beroa eman zaio, era kuasiestatikoan, bere presioa $2p_0$ izan arte.

Lortu:

1. Eskuineko guneko gasaren entropia-aldaketa eta barne-energiaren aldaketa.

2. Ezkerreko gasaren entropia-aldaketa, barne-energiaren aldaketa eta xurgatu duen beroa.

Emaitza

Ebazpen posible bat…

irudi-oina

---

Testuingurua

15. ARIKETA

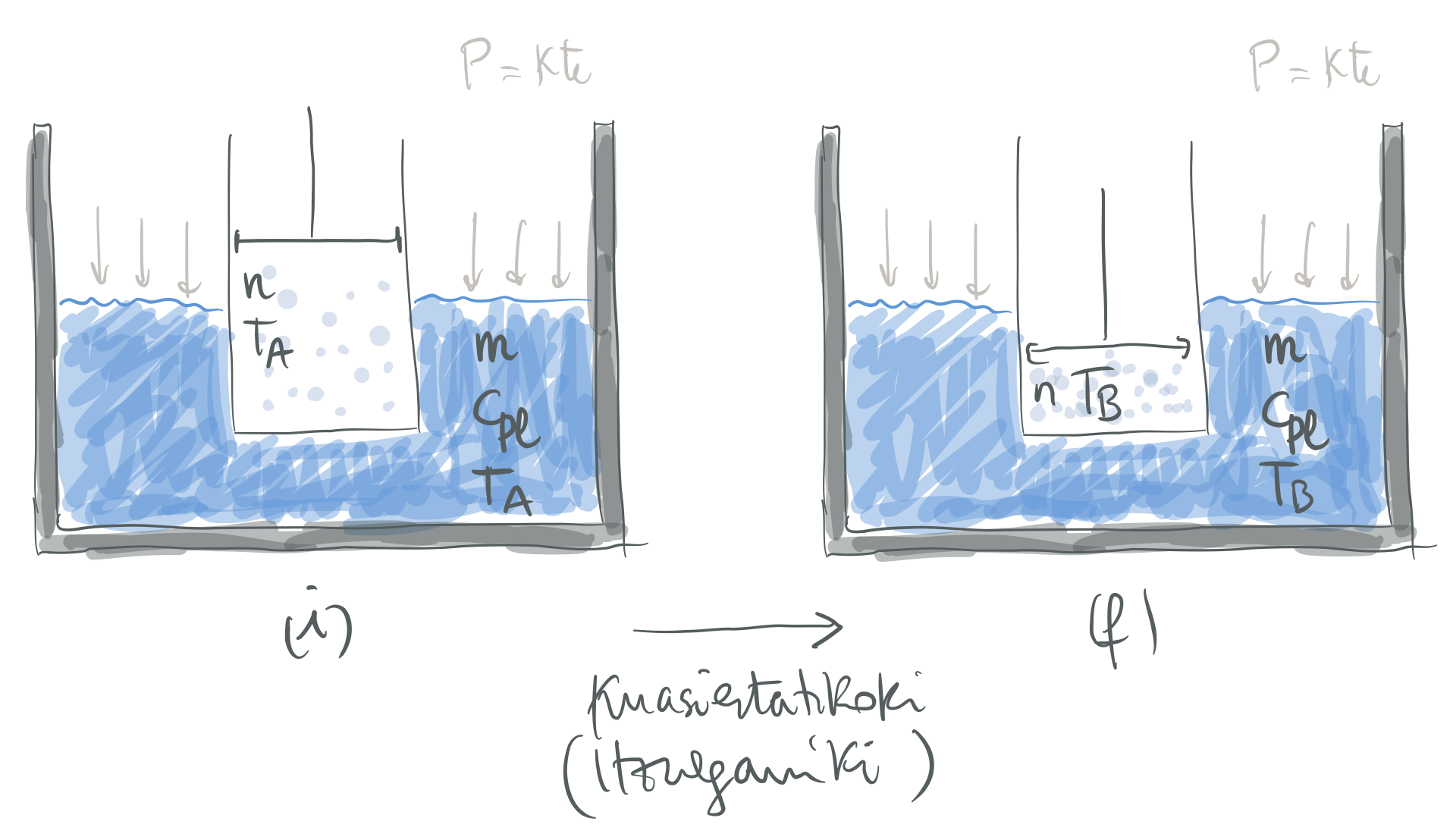
Esku artean dugun sistema irudian ageri dena da: horma guztiak adiabatikoak, higiezinak eta iragaztezinak dituen zilindroa, ezkerrekoa izan ezik, diatermoa bera. Irudian ikus daitekeenez, zilindroaren barnean, higikorra, adiabatikoa eta iragaztezina den pistoia dago. Pistoiak banatu dituen zilindroaren bi guneek van der Waals-en gasaren mol bana dute. Ezkerreko aldean dagoen gasari beroa eman zaio, era kuasiestatikoan, bukaerako tenperatura eta bolumena $T_2$ eta $\frac{3v_0}{2}$, hurrenez hurren, izan arte. Gasaren $C_V$ eta $C_p$ bero-ahalmenak ezagunak dira eta ez dute tenperaturarekiko mendekotasunik.
Hasierako egoera ondoko hau da:

Eskuineko gunea: $v_0$. Ezkerreko gunea: $T_0$, $v_0$, $p_0$

Lortu:

1. gune bietako gasaren entropia-aldaketa,

2. ezkerreko aldeko gasaren barne-energiaren aldaketa,

3. horrek jaso duen bero kantitatea eta egindako lana.

Emaitza

Ebazpen posible bat…

---

Testuingurua

16. ARIKETA

Esku artean gas ideal baten 1 mol-eko lagina dugu. 25 ${}^{\circ }$C-an dagoen bero-iturriarekin ukipenean dagoela, 100 atm-tik 1 atm-erako espantsioa eragin diogu laginari.

Lortu unibertsoaren entropia-aldaketa honako bi kasu hauetan:

1. Lanik egin ez bada.

2. Egindako lana 2980 joule izan bada.

Emaitza

Ebazpen posible bat…

---

Testuingurua

17. ARIKETA

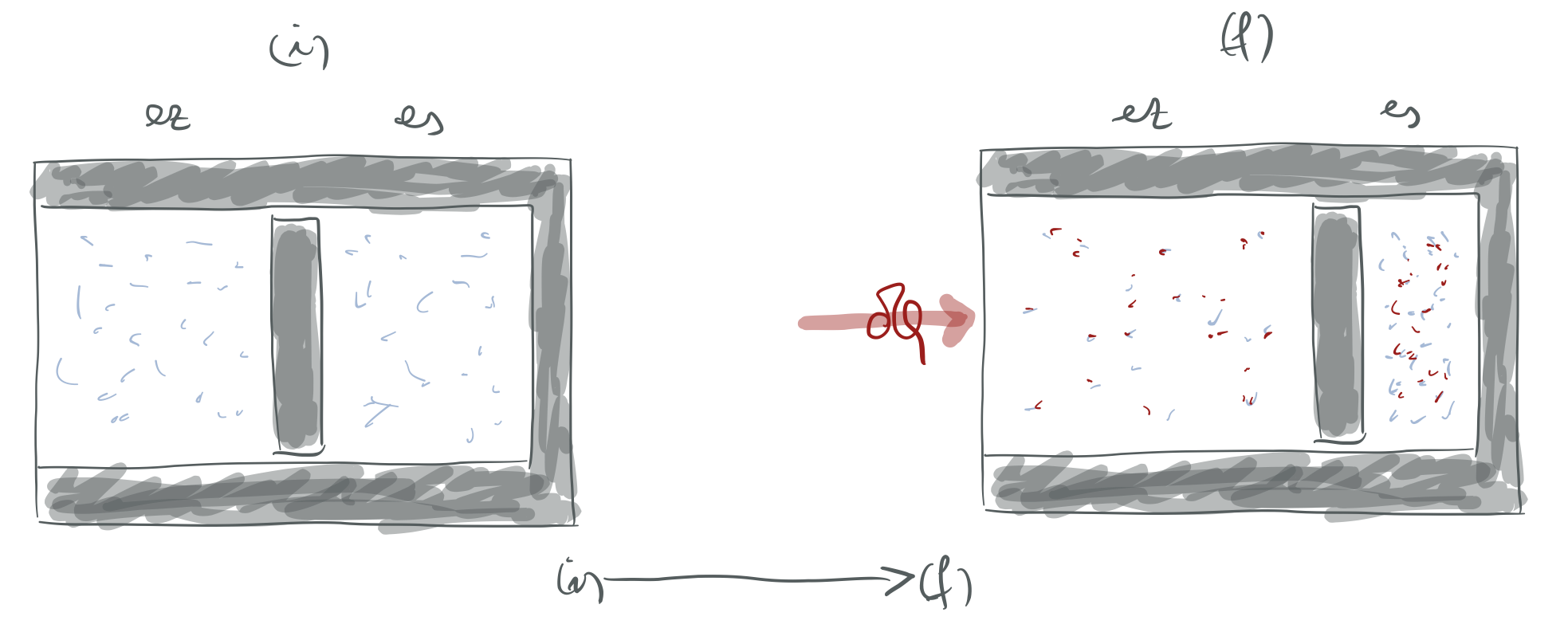
Bereizte-horma diatermoak eta higikorrak $V_A$ eta $V_B$ hasierako bolumeneko bi guneetan banatu ditu. Guneek gas ideal baten mol bana dute eta hasierako egoera berean daude: $T$ tenperaturako egoera termikoan.

Frogatu, bukaerako oreka-egoera lortutakoan, guneei (sistema konposatu moduan) dagokien entropia-aldaketa ondoko hau dela:

$$\mathrm{\Delta }S=R\ln \left\{\frac{(V_A+V_B{)}^2}{4V_A{V}_B}\right\}$$

Emaitza

Ebazpen posible bat…

---

Testuingurua

18. ARIKETA

10 eta 15 l-ko gordailuak finkoa, adiabatikoa eta iragaztezina den hormak banandu ditu. Lehenengo gunean SO${}_2$ gasa sartu dugu: 288 K-ean eta 2 atm-n. Bigarrenean, NO gasa; kasu honetan, 300 K-ean eta 1 atm-n.

1. Diatermano eta higikor bihurtu dugu bereizte-horma.
   Lortu sistema osoari dagokion entropia-aldaketa.

2. Hasierako baldintzetatik abiatuz, bereizte-horma bat-batean kendu dugu.
   Lortu sistema osoari dagokion entropia-aldaketa.

3. Gordailuetako gasak berdinak izanik, nola aldatuko lirateke aurreko emaitzak?

Emaitza

Ebazpen posible bat…

---

Testuingurua

19. ARIKETA

Esku artean dugun hari elastikoa $1,5L_0$ luzera lortu arte luzatu dugu, era itzulgarrian. $L_0$ da hasierako luzera. Inguruneko tenperatura 27${}^{\circ }$ C da eta, aipatutako prozesuan, hariak 1000 J xurgatu du, ingurunetik. Luzapenaren ondoren, hari elastikoa askatu dugu eta hasierako luzera berreskuratu du, era itzulgarrian. Azken prozesu horretan 2600 J-ko lana egin du sistemak.

Lortu honako hauek:

1. Hariaren entropia-aldaketa, luzatutakoan.

2. Hariaren entropia-aldaketa, bigarren prozesuaren ondorioz.

3. Unibertsoaren entropia-aldaketa, bi prozesuen ondorioz.

4. Luzapenean egindako lana.

Emaitza

1. $\mathrm{\Delta }{S}_{i\to f}^{\text{sis}}=\frac{Q^{\text{sis}}}{T^{\text{bi}}}$

Ebazpen posible bat…

---

Testuingurua

20. ARIKETA

Aztertu beharreko gas erreala era askean zabaldu da, $T=300$ K-eko bero-iturriarekin ukipen termikoan. Prozesu horretan xurgatu duen beroa da $Q=50$ J. Lehenengo prozesu horren ondoren, gasa konprimitu dugu, era isotermo itzulgarrian; hasierako egoera berreskuratu arte. Bigarren prozesu horretan, gasak 300 J kanporatu du.

Lortu honako hauek:

1. Gasaren entropia-aldaketa, lehenengo prozesuan.

2. Gasak egindako lana, bigarren prozesuan.

Emaitza

1. $\mathrm{\Delta }{S}_{i\to f}^{\text{sis}}=\frac{10}{3}\frac{\text{J}}{\text{K}}$

$\mathrm{\Delta }{W}_{f\to i}^{\text{sis}}=-Q_{i\to f}^{\text{sis}}-Q_{f\to i}^{\text{sis}}$

Ebazpen posible bat…

---

Lan Maximoa

Testuingurua

21. ARIKETA

Meteorito batek, $4\times {10}^4$ tonakoa bera, Lurraren kontra jo du eta Lurraren gainazalean geratu da.

Lortu meteoritotik atera daitekeen lan maximoa, eguratsaren tenperatura 30 ${}^{\circ }$C bada, meteoritoaren tenperatura 2000 ${}^{\circ }$C dela jakinik, eta bere bero-ahalmen espezifikoa (presioa konstantea denean) honako hau dela jakinik: $c_p=0.42+4.2\times {10}^{-5}$ T (JK${}^{-1}$g${}^{-1}$).

Emaitza

Ebazpen posible bat…

---

Testuingurua

22. ARIKETA

1. A sistema, $C$ bero-ahalmenekoa bera, $T_2$ tenperaturan dago. Makina termiko idealaren bidez ingurunearekin ukipenean ezarri da; ingurunearen tenperatura $T_1>T_2$ da.

   Lortu sistematik atera daitekeen $W$ lan maximoa.

2. Ondoren, $W$ lana A sistema berotzeko erabiliko da. Frogatu sistemak lor dezakeen $T_3$ tenperaturarik altuena $W$ lan maximoarekin ondoko adierazpenaren bidez erlazionaturik dagoela:

   $T_3-T_2[1+\ln \left({\displaystyle \frac{T_3}{T_2}}\right)]={\displaystyle \frac{W}{C}}$

Emaitza

Ebazpen posible bat…

---

Testuingurua

23. ARIKETA

Ondokoak dira aztertu beharreko bi sistemen bero-ahalmenak: $C_A=64$ cal/K${}^{-1}$ eta $C_B=93.5$ cal/K${}^{-1}$. Sistemen hasierako tenperaturak $T_A$ eta $T_B$ dira, hurrenez hurren. Ukipen diatermoan jarriz, sistema konposatua eratu da.

Lortu bukaerako tenperatura honako kasuetan:

1. Ukipena era itzulezinean gertatu da.

2. Ukipena era itzulgarrian gertatu da eta atera daitekeen lan maximoa.

Emaitza

Ebazpen posible bat…

---

Testuingurua

24. ARIKETA

Esku artean dugun sistemari esleitu zaion egoera-ekuazioa ondokoa da:

$$pV=RT+C{p}^2$$

Hauxe da sistemaren hasierako egoera: (600 K, 100 atm).
300 K-ean dagoen bero-iturria erabilgarria da eta sistemaren bukaerako egoera honako hau: (300 K, 1 atm).

Lortu:

1. Prozesuaren ondoriozko sistemaren entropia-aldaketa eta barne-energiaren aldaketa.

2. Egoera biak lotzean atera daitekeen lan maximoa.

Sistemaren $c_p$ bero-ahalmena $3R$ da.

Emaitza

Ebazpen posible bat…

---

Testuingurua

25. ARIKETA

Berdinak diren bi sistemen bero-ahalmenek honako ekuazioari segitu diote: $C=2BT$, non $B=2\cdot {10}^{-2}$ J$/$K${}^2$ den.

Sistemen tenperaturak 200 K eta 400 K dira, hurrenez hurren. Ukipen diatermoan ezarriz gero, lortu unibertsoaren entropia-aldaketa eta lan maximoa.

Emaitza

Ebazpen posible bat…

---

Testuingurua

26. ARIKETA

Esku artean $C_V$ bero-ahalmeneko $N$ sistema berdin ditugu; beren tenperaturak $\{T_1,T_2,\dots T_N\}$ dira.

1. Besterik gabe, elkarren arteko ukipen termikoan jarri dira.
   Zenbatekoa da trukatu duten bero kantitate osoa?

2. Demagun, ondoren, $T_0$ tenperaturan dagoen bero-iturria erabilgarri dela eta horrekin ukipen termikoan jarri direla sistemak.
   Zenbatekoa da horrelako egoeratik atera daitekeen lan maximoa?
   Jakina, lortu sistemen bukaerako oreka-egoera termikoa, arestian aipatutako bi kasuetan

Emaitza

Ebazpen posible bat…

---